Correlación angular perturbada

Sonda nuclear en una red.

Esquema de espectroscopia PAC

La correlación angular perturbada γ-γ , PAC o espectroscopia PAC , es un método de física nuclear del estado sólido con el que se pueden medir los campos magnéticos y eléctricos en estructuras cristalinas . Al hacerlo, se determinan los gradientes de campo eléctrico y la frecuencia de Larmor en campos magnéticos, así como los efectos dinámicos. Con este método muy sensible, que requiere solo alrededor de 10-1000 mil millones de átomos de un isótopo radiactivo por medición, se pueden investigar las propiedades del material en la estructura local , las transiciones de fase, el magnetismo y la difusión. El método PAC está relacionado con la resonancia magnética nuclear y el efecto Mössbauer , pero no muestra atenuación de señal a temperaturas muy altas. Hoy en día solo se utiliza la correlación angular perturbada diferencial en el tiempo ( TDPAC ).

Historia y desarrollo

Medición de coincidencia en representación simplificada.

El PAC se remonta a un trabajo teórico de Donald R. Hamilton ^[1] de 1940. El primer experimento exitoso fue llevado a cabo por Brady y Deutsch ^[2] en 1947. En estos primeros experimentos de PAC se investigaron esencialmente el espín y la paridad de los espines nucleares. Sin embargo, se reconoció pronto que los campos eléctricos y magnéticos interactúan con el momento nuclear, ^[3] proporcionando la base para una nueva forma de investigación de materiales: la espectroscopia nuclear de estado sólido.

Paso a paso se fue desarrollando la teoría. ^{[4] [5] [6] [7] [8] [ 9] [10] [11] [12] [13] [14] [15] [16] [17]} Después de que Abragam y Pound ^[18] publicaran su trabajo sobre la teoría del PAC en 1953 incluyendo campos nucleares extra, muchos estudios con PAC se llevaron a cabo posteriormente. En los años 1960 y 1970, el interés en los experimentos de PAC aumentó drásticamente, centrándose principalmente en los campos magnéticos y eléctricos en cristales en los que se introdujeron los núcleos de la sonda. A mediados de los años 1960, se descubrió la implantación de iones, proporcionando nuevas oportunidades para la preparación de muestras. El rápido desarrollo electrónico de los años 1970 trajo consigo mejoras significativas en el procesamiento de señales. Desde la década de 1980 hasta la actualidad, el PAC ha surgido como un método importante para el estudio y caracterización de materiales, ^{[19] [20] [21] [22] [23]} por ejemplo para el estudio de materiales semiconductores, compuestos intermetálicos, superficies e interfaces, y también han aparecido varias aplicaciones en bioquímica. ^[24]

Si bien hasta aproximadamente 2008 los instrumentos PAC utilizaban electrónica de alta frecuencia convencional de la década de 1970, en 2008 Christian Herden y Jens Röder et al. desarrollaron el primer instrumento PAC completamente digitalizado que permite un análisis de datos extenso y el uso paralelo de múltiples sondas. ^[25] Siguieron réplicas y desarrollos posteriores. ^{[26] [27]}

Principio de medición

Esquema de desintegración de ¹¹¹ In a ¹¹¹ Cd.

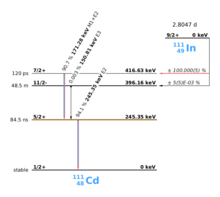
El PAC utiliza sondas radiactivas que tienen un estado intermedio con tiempos de desintegración de 2 ns a aproximadamente 10 μs, véase el ejemplo ¹¹¹ In en la imagen de la derecha. Después de la captura de electrones (EC), el indio se transmuta en cadmio. Inmediatamente después, el núcleo de cadmio ¹¹¹ se encuentra predominantemente en el espín nuclear excitado 7/2+ y solo en una medida muy pequeña en el espín nuclear 11/2-, este último no debe considerarse más. El estado excitado 7/2+ pasa al estado intermedio 5/2+ emitiendo un γ-quantum de 171 keV. El estado intermedio tiene una vida útil de 84,5 ns y es el estado sensible para el PAC. Este estado a su vez se desintegra en el estado fundamental 1/2+ emitiendo un γ-quantum con 245 keV. El PAC ahora detecta ambos γ-quantum y evalúa el primero como señal de inicio, el segundo como señal de parada.

Espectros individuales en 90° y 180° que muestran el efecto de perturbación.

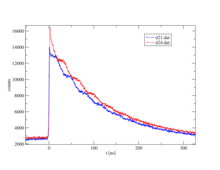
Ahora se mide el tiempo entre el inicio y el final de cada evento. Esto se llama coincidencia cuando se ha encontrado un par de inicio y final. Dado que el estado intermedio se desintegra según las leyes de la desintegración radiactiva, se obtiene una curva exponencial con la duración de este estado intermedio después de trazar la frecuencia en el tiempo. Debido a la radiación no esféricamente simétrica del segundo γ-quantum, la llamada anisotropía, que es una propiedad intrínseca del núcleo en esta transición, llega a un desorden periódico ( interacción hiperfina ) con los campos eléctricos y/o magnéticos circundantes. La ilustración de los espectros individuales a la derecha muestra el efecto de esta perturbación como un patrón de onda en la desintegración exponencial de dos detectores, un par a 90° y otro a 180° entre sí. Las formas de onda de ambos pares de detectores están desplazadas entre sí. Muy simplemente, uno puede imaginar un observador fijo mirando un faro cuya intensidad de luz se vuelve periódicamente más clara y más oscura. En consecuencia, una disposición de detectores, normalmente cuatro detectores en una disposición plana de 90° o seis detectores en una disposición octaédrica, "ve" la rotación del núcleo en el orden de magnitud de MHz a GHz.

Abajo: un espectro PAC complejo, arriba: su transformación de Fourier.

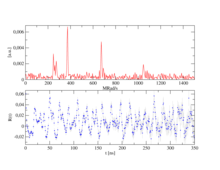
En función del número n de detectores, se obtiene el número de espectros individuales (z) después de z=n²-n, es decir, para n=4, 12 y para n=6, 30. Para obtener un espectro PAC, los espectros individuales de 90° y 180° se calculan de tal manera que las funciones exponenciales se cancelen entre sí y, además, las diferentes propiedades del detector se acorten. La función de perturbación pura permanece, como se muestra en el ejemplo de un espectro PAC complejo. Su transformada de Fourier proporciona las frecuencias de transición como picos.

${\displaystyle R(t)}$, la relación de velocidad de conteo, se obtiene a partir de los espectros individuales utilizando:

${\displaystyle R(t)=2{\frac {W(180^{\circ },t)-W(90^{\circ },t)}{W(180^{\circ },t)+2W(90^{\circ },t)}}}$

Dependiendo del espín del estado intermedio, se observa un número diferente de frecuencias de transición. Para un espín 5/2, se pueden observar 3 frecuencias de transición con la relación ω ₁ +ω ₂ =ω ₃ . Como regla, se puede observar una combinación diferente de 3 frecuencias para cada sitio asociado en la celda unitaria.

Espectro PAC de ZnO monocristal con ajuste.

El PAC es un método estadístico: cada átomo de sonda radiactiva se encuentra en su propio entorno. En los cristales, debido a la alta regularidad de la disposición de los átomos o iones, los entornos son idénticos o muy similares, de modo que las sondas en sitios reticulares idénticos experimentan el mismo campo hiperfino o campo magnético, que luego se vuelve medible en un espectro PAC. Por otro lado, para sondas en entornos muy diferentes, como en materiales amorfos, generalmente se observa una distribución de frecuencia amplia o nula y el espectro PAC parece plano, sin respuesta de frecuencia. Con monocristales, dependiendo de la orientación del cristal con respecto a los detectores, ciertas frecuencias de transición pueden reducirse o extinguirse, como se puede ver en el ejemplo del espectro PAC del óxido de zinc (ZnO).

Configuración instrumental

Configuración instrumental de detectores alrededor de la sonda.

Espectro energético de ¹⁴⁹ Gd con ventanas de energía para arranque y parada.

En el espectrómetro PAC típico, se coloca una configuración de cuatro detectores en matriz plana de 90° y 180° o seis detectores en matriz octaédrica alrededor de la muestra de fuente radiactiva. Los detectores utilizados son cristales de centelleo de BaF ₂ o NaI. En los instrumentos modernos de hoy en día se utilizan principalmente LaBr ₃ :Ce o CeBr _3. Los fotomultiplicadores convierten los destellos débiles de luz en señales eléctricas generadas en el centelleador por la radiación gamma. En los instrumentos clásicos, estas señales se amplifican y procesan en circuitos lógicos AND/OR en combinación con ventanas de tiempo, las diferentes combinaciones de detectores (para 4 detectores: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43) se asignan y cuentan. Los espectrómetros digitales modernos utilizan tarjetas digitalizadoras que utilizan directamente la señal y la convierten en valores de energía y tiempo y los almacenan en discos duros. A continuación, el software busca coincidencias en estos datos. Mientras que en los instrumentos clásicos es necesario establecer "ventanas" que limiten las respectivas energías γ antes del procesamiento, en el PAC digital esto no es necesario durante el registro de la medición. El análisis solo se realiza en el segundo paso. En el caso de sondas con cascadas complejas, esto permite realizar una optimización de datos o evaluar varias cascadas en paralelo, así como medir diferentes sondas simultáneamente. Los volúmenes de datos resultantes pueden estar entre 60 y 300 GB por medición.

Materiales de muestra

En principio, como materiales de investigación (muestras) se pueden utilizar todos los materiales que pueden ser sólidos o líquidos. Según la pregunta y el propósito de la investigación, se dan ciertas condiciones marco. Para la observación de frecuencias de perturbación claras es necesario, debido al método estadístico, que una determinada proporción de los átomos de la sonda se encuentren en un entorno similar y, por ejemplo, experimenten el mismo gradiente de campo eléctrico. Además, durante el intervalo de tiempo entre el inicio y la parada, o aproximadamente 5 vidas medias del estado intermedio, la dirección del gradiente de campo eléctrico no debe cambiar. En los líquidos, por lo tanto, no se puede medir ninguna frecuencia de interferencia como resultado de las colisiones frecuentes, a menos que la sonda esté complejada en moléculas grandes, como en las proteínas. Las muestras con proteínas o péptidos generalmente se congelan para mejorar la medición.

Los materiales más estudiados con PAC son sólidos como semiconductores, metales, aislantes y varios tipos de materiales funcionales. Para las investigaciones, estos suelen ser cristalinos. Los materiales amorfos no tienen estructuras altamente ordenadas. Sin embargo, tienen una proximidad cercana, lo que se puede ver en la espectroscopia PAC como una amplia distribución de frecuencias. Los nanomateriales tienen un núcleo cristalino y una capa que tiene una estructura más bien amorfa. Esto se llama modelo núcleo-capa. Cuanto más pequeña se vuelve la nanopartícula, mayor se vuelve la fracción de volumen de esta porción amorfa. En las mediciones PAC, esto se muestra por la disminución del componente de frecuencia cristalina en una reducción de la amplitud (atenuación).

Preparación de muestras

La cantidad de isótopos de PAC adecuados necesarios para una medición oscila entre 10 y 1000 mil millones de átomos (10 ¹⁰ -10 ¹² ). La cantidad correcta depende de las propiedades particulares del isótopo. 10 mil millones de átomos son una cantidad muy pequeña de sustancia. A modo de comparación, un mol contiene aproximadamente 6,22x10 ²³ partículas. 10 ¹² átomos en un centímetro cúbico de berilio dan una concentración de aproximadamente 8 nmol/L (nanomol=10 ⁻⁹ mol). Las muestras radiactivas tienen cada una una actividad de 0,1-5 MBq, que está en el orden del límite de exención para el isótopo respectivo.

La forma de introducir los isótopos de PAC en la muestra que se va a analizar depende del experimentador y de las posibilidades técnicas. Los métodos habituales son los siguientes:

Implantación

Esquema del dispositivo separador de isótopos en línea ( ISOLDE ) del CERN . El haz de protones de los propulsores sincrotrón de protones (PSB) crea por fisión en los núcleos radiactivos diana. Estos se ionizan en fuentes de iones, se aceleran y, debido a sus diferentes masas, se separan mediante separadores de masa magnéticos, ya sea por GPS ( separador de propósito general ) o HRS ( separador de alta resolución ).

Durante la implantación se genera un haz de iones radiactivos que se dirige hacia el material de muestra. Debido a la energía cinética de los iones (1-500 keV), estos se dirigen hacia la red cristalina y se frenan con los impactos. O bien se detienen en los puntos intersticiales o bien empujan un átomo de la red y lo sustituyen. Esto provoca una alteración de la estructura cristalina. Estas alteraciones se pueden investigar con PAC. Mediante el templado de estas alteraciones se pueden corregir. Si, por el contrario, se deben examinar los defectos de radiación en el cristal y su reparación, se miden las muestras no detectadas, que luego se recocen paso a paso.

La implantación suele ser el método de elección, ya que permite obtener muestras muy bien definidas.

Evaporación

En el vacío, la sonda de PAC se puede evaporar sobre la muestra. La sonda radiactiva se aplica a una placa o filamento calefactor, donde se lleva a la temperatura de evaporación y se condensa sobre el material de muestra opuesto. Con este método, por ejemplo, se examinan superficies. Además, mediante la deposición en fase de vapor de otros materiales, se pueden generar interfases. Se pueden estudiar durante el templado con PAC y se pueden observar sus cambios. De manera similar, la sonda de PAC se puede transferir a la pulverización catódica utilizando un plasma.

Difusión

En el método de difusión, la sonda radiactiva se suele diluir en un disolvente aplicado a la muestra, se seca y se difunde en el material mediante atemperado. La solución con la sonda radiactiva debe ser lo más pura posible, ya que todas las demás sustancias pueden difundirse en la muestra y afectar así a los resultados de la medición. La muestra debe estar suficientemente diluida en la muestra. Por lo tanto, el proceso de difusión debe planificarse de modo que se logre una distribución uniforme o una profundidad de penetración suficiente.

Añadido durante la síntesis

Las sondas de PAC también se pueden añadir durante la síntesis de los materiales de muestra para lograr la distribución más uniforme en la muestra. Este método es especialmente adecuado si, por ejemplo, la sonda de PAC se difunde poco en el material y se espera una mayor concentración en los límites de grano. Dado que con PAC solo se necesitan muestras muy pequeñas (aproximadamente 5 mm), se pueden utilizar microrreactores. Lo ideal es añadir la sonda a la fase líquida del proceso sol-gel o a una de las fases precursoras posteriores.

Activación de neutrones

En la activación neutrónica , la sonda se prepara directamente a partir del material de muestra convirtiendo una parte muy pequeña de uno de los elementos del material de muestra en la sonda PAC deseada o su isótopo original mediante captura de neutrones. Al igual que con la implantación, el daño por radiación debe repararse. Este método está limitado a materiales de muestra que contienen elementos a partir de los cuales se pueden fabricar sondas PAC de captura de neutrones. Además, las muestras pueden contaminarse intencionalmente con aquellos elementos que se van a activar. Por ejemplo, el hafnio es excelente para la activación debido a su gran sección transversal de captura de neutrones.

Reacción nuclear

En raras ocasiones se utilizan reacciones nucleares directas en las que los núcleos se convierten en sondas PAC mediante el bombardeo de partículas elementales de alta energía o protones. Esto provoca importantes daños por radiación que deben repararse. Este método se utiliza con PAD, que pertenece a los métodos PAC.

Laboratorios

El mayor laboratorio de PAC del mundo en la actualidad se encuentra en ISOLDE en el CERN , con unos 10 instrumentos PAC, que recibe su principal financiación del BMBF . Los haces de iones radiactivos se generan en ISOLDE bombardeando protones desde el propulsor sobre materiales objetivo (carburo de uranio, estaño líquido, etc.) y evaporando los productos de espalación a altas temperaturas (hasta 2000 °C), para luego ionizarlos y acelerarlos. Con la posterior separación de masas se pueden producir haces de isótopos generalmente muy puros, que se pueden implantar en muestras de PAC. De particular interés para el PAC son las sondas isoméricas de vida corta como: ^111m Cd, ^199m Hg, ^204m Pb y varias sondas de tierras raras.

Teoría

Cascada general γ-γ con tiempo de vida del estado intermedio. ${\displaystyle \tau _{N}}$

El primer cuanto ( ) se emitirá de forma isotrópica. Al detectar este cuanto en un detector se selecciona un subconjunto con una orientación de las muchas direcciones posibles que tiene un determinado. El segundo cuanto ( ) tiene una emisión anisotrópica y muestra el efecto de la correlación angular. El objetivo es medir la probabilidad relativa con la detección de en el ángulo fijo en relación con . La probabilidad se da con la correlación angular ( teoría de perturbaciones ): ${\displaystyle \gamma }$ ${\displaystyle \gamma _{1},k_{1}}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma _{2},k_{2}}$ ${\displaystyle W(\Theta ){\textrm {d}}(\Omega )}$ ${\displaystyle \gamma _{2}}$ ${\displaystyle \Theta }$ ${\displaystyle \gamma _{1}}$

${\displaystyle W(\Theta )=\sum _{k}^{k_{max}}A_{kk}P_{k}cos(\Theta )}$

Para una - -cascada, se debe a la preservación de la paridad : ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle k}$

${\displaystyle 0<k<{\textrm {min}}(2I_{S},I_{i}+I'_{i})}$

Donde es el espín del estado intermedio y con la multipolaridad de las dos transiciones. Para transiciones multipolares puras, es . ${\displaystyle I_{S}}$ ${\displaystyle I_{i}}$ ${\displaystyle i=1;2}$ ${\displaystyle I_{i}=I'_{i}}$

${\displaystyle A_{kk}}$es el coeficiente de anisotropía que depende del momento angular del estado intermedio y de las multipolaridades de la transición.

El núcleo radiactivo está integrado en el material de muestra y emite dos cuantos al desintegrarse. Durante la vida útil del estado intermedio, es decir, el tiempo entre y , el núcleo experimenta una perturbación debido a la interacción hiperfina a través de su entorno eléctrico y magnético. Esta perturbación cambia la correlación angular a: ${\displaystyle \gamma }$ ${\displaystyle \gamma _{1}}$ ${\displaystyle \gamma _{2}}$

${\displaystyle W(\Theta )=\sum _{k}^{k_{max}}A_{kk}G_{kk}}$

${\displaystyle G_{kk}}$es el factor de perturbación. Debido a la interacción eléctrica y magnética, el momento angular del estado intermedio experimenta un par de torsión alrededor de su eje de simetría. Desde el punto de vista de la mecánica cuántica, esto significa que la interacción conduce a transiciones entre los estados M. El segundo -cuanto ( ) se envía entonces desde el nivel intermedio. Este cambio de población es la razón de la atenuación de la correlación. ${\displaystyle I_{i}}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma _{2}}$

La interacción se produce entre el momento dipolar del núcleo magnético y el estado intermedio o/y un campo magnético externo . La interacción también se produce entre el momento cuadrupolar nuclear y el gradiente del campo eléctrico externo al núcleo . ${\displaystyle {\vec {\nu }}}$ ${\displaystyle I_{S}}$ ${\displaystyle {\vec {B}}}$ ${\displaystyle V_{zz}}$

Interacción dipolar magnética

Para la interacción dipolar magnética, la frecuencia de la precesión del espín nuclear alrededor del eje del campo magnético viene dada por: ${\displaystyle {\vec {B}}}$

${\displaystyle \omega _{L}={\frac {g\cdot u_{N}\cdot B}{\hbar }}}$

${\displaystyle \Delta E=\hbar \cdot \omega _{L}=-g\cdot u_{N}\cdot B}$

${\displaystyle g}$es el factor g de Landé y es el magnetón nuclear . ${\displaystyle u_{N}}$

Con lo siguiente: ${\displaystyle N=M-M'}$

${\displaystyle E_{magn}(M)-E_{magn}(M')=-(M-M')g\mu _{N}B_{z}=N\hbar \omega _{L}}$

De la teoría general obtenemos:

${\displaystyle G_{k_{1}k_{2}}^{NN}={\sqrt {(2k_{1}+1)(2k_{2}+1)}}\cdot e^{-iN\omega _{L}t}\times \sum _{M}{\begin{pmatrix}I&I&k_{1}\\M'&-M&N\\\end{pmatrix}}{\begin{pmatrix}I&I&k_{2}\\M'&-M&N\\\end{pmatrix}}}$

Para la interacción magnética se cumple:

${\displaystyle G_{k_{1}k_{2}}^{NN}=e^{\left({-iN\omega _{L}t}\right)}}$

Interacción cuadrupolo-eléctrica estática

La energía de la interacción eléctrica hiperfina entre la distribución de carga del núcleo y el campo eléctrico estático extranuclear se puede extender a multipolos. El término monopolar sólo provoca un desplazamiento de energía y el término dipolar desaparece, de modo que el primer término de expansión relevante es el término cuadrupolar:

${\displaystyle E_{Q}=\sum _{ij}Q_{ij}V_{ij}}$     ij=1;2;3

Esto se puede escribir como un producto del momento cuadrupolar y el gradiente del campo eléctrico . Ambos tensores son de segundo orden. Los órdenes superiores tienen un efecto demasiado pequeño para medirse con PAC. ${\displaystyle Q_{ij}}$ ${\displaystyle V_{ij}}$

El gradiente del campo eléctrico es la segunda derivada del potencial eléctrico en el núcleo: ${\displaystyle \Phi ({\vec {r}})}$

${\displaystyle V_{ij}={\frac {\partial ^{2}\Phi ({\vec {r}})}{\partial x_{i}\partial x_{j}}}={\begin{pmatrix}V_{xx}&0&0\\0&V_{yy}&0\\0&0&V_{zz}\\\end{pmatrix}}}$

${\displaystyle V_{ij}}$se diagonaliza, que:

${\displaystyle |V_{zz}|\geq |V_{yy}|\geq |V_{xx}|}$

La matriz está libre de trazas en el sistema de ejes principal ( ecuación de Laplace )

${\displaystyle V_{xx}+V_{yy}+V_{zz}=0}$

Normalmente, el gradiente del campo eléctrico se define con la mayor proporción y : ${\displaystyle V_{zz}}$ ${\displaystyle \eta }$

${\displaystyle \eta ={\frac {V_{yy}-V_{xx}}{V_{zz}}}}$,         ${\displaystyle 0\leq \eta \leq 1}$

En los cristales cúbicos, los parámetros del eje de la celda unitaria x, y, z tienen la misma longitud. Por lo tanto:

${\displaystyle V_{zz}=V_{yy}=V_{xx}}$y ${\displaystyle \eta =0}$

En sistemas axisimétricos es . ${\displaystyle \eta =0}$

Para gradientes de campo eléctrico axialmente simétricos, la energía de los subestados tiene los valores:

${\displaystyle E_{Q}={\frac {eQV_{zz}}{4I(2I-1)}}\cdot (3m^{2}-I(I+1))}$

La diferencia de energía entre dos subestados, y , viene dada por: ${\displaystyle M}$ ${\displaystyle M'}$

${\displaystyle \Delta E_{Q}=E_{m}-E_{m'}={\frac {eQV_{zz}}{4I(2I-1)}}\cdot 3|M^{2}-M'^{2}|}$

Se introduce la frecuencia cuadripolar . Las fórmulas en los cuadros de colores son importantes para la evaluación: ${\displaystyle \omega _{Q}}$

${\displaystyle \omega _{Q}={\frac {eQV_{zz}}{4I(2I-1)\hbar }}={\frac {2\pi eQV_{zz}}{4I(2I-1)h}}={\frac {2\pi \nu _{Q}}{4I(2I-1)}}}$

${\displaystyle \nu _{Q}={\frac {eQ}{h}}V_{zz}={\frac {4I(2I-1)\omega _{Q}}{2\pi }}}$

Las publicaciones en su mayoría enumeran . como carga elemental y como constante de Planck son bien conocidos o bien definidos. El momento cuadrupolar nuclear a menudo se determina solo de manera muy imprecisa (a menudo solo con 2-3 dígitos). Debido a que se puede determinar con mucha más precisión que , no es útil especificarlo solo debido a la propagación del error. Además, ¡ es independiente del espín! Esto significa que se pueden comparar las mediciones de dos isótopos diferentes del mismo elemento, como ^199m Hg(5/2−), ^197m Hg(5/2−) y ^201m Hg(9/2−). Además, se puede utilizar como método de huella digital. ${\displaystyle \nu _{Q}}$ ${\displaystyle e}$ ${\displaystyle h}$ ${\displaystyle Q}$ ${\displaystyle \nu _{Q}}$ ${\displaystyle Q}$ ${\displaystyle V_{zz}}$ ${\displaystyle \nu _{Q}}$ ${\displaystyle \nu _{Q}}$

Para la diferencia de energía se tiene entonces:

${\displaystyle \Delta E_{Q}=\hbar \omega _{Q}\cdot 3|m^{2}-m'^{2}|}$

Si , entonces: ${\displaystyle \eta =0}$

${\displaystyle \omega ^{n}=n\cdot \omega _{Q}^{0}}$

con:

${\displaystyle \omega _{Q}^{0}={\textrm {min}}\left({\frac {\Delta E_{Q}}{\hbar }}\right)}$

Para giros enteros se aplica:

${\displaystyle \omega _{Q}^{0}=3\cdot \omega _{Q}}$         y          ${\displaystyle n=|M^{2}-M'^{2}|}$

Para giros de medio entero se aplica:

${\displaystyle \omega _{Q}^{0}=6\cdot \omega _{Q}}$          y          ${\displaystyle n={\frac {1}{2}}|M^{2}-M'^{2}|}$

El factor de perturbación viene dado por:

${\displaystyle G_{k_{1}k_{2}}^{NN}=\sum _{n}s_{nN}^{k_{1}k_{2}}\cos {(n\omega _{Q}^{0}t)}}$

Con el factor de probabilidades de las frecuencias observadas:

${\displaystyle s_{nN}^{k_{1}k_{2}}={\sqrt {(2k_{1}+1)(2k_{2}+1)}}\cdot \sum _{M,M'}{\begin{pmatrix}I&I&k_{1}\\M'&-M&N\\\end{pmatrix}}{\begin{pmatrix}I&I&k_{2}\\M'&-M&N\\\end{pmatrix}}}$

En lo que respecta a la interacción dipolar magnética, la interacción cuadrupolar eléctrica también induce una precisión de la correlación angular en el tiempo y esto modula la frecuencia de interacción cuadrupolar. Esta frecuencia es una superposición de las diferentes frecuencias de transición . Las amplitudes relativas de los diversos componentes dependen de la orientación del gradiente de campo eléctrico con respecto a los detectores (eje de simetría) y del parámetro de asimetría . Para una sonda con diferentes núcleos de sonda, se necesita un parámetro que permita una comparación directa: por lo tanto, se introduce la constante de acoplamiento cuadrupolar independiente del espín nuclear . ${\displaystyle \omega _{n}}$ ${\displaystyle \eta }$ ${\displaystyle \nu _{Q}}$ ${\displaystyle {\vec {I}}}$

Interacciones combinadas

Si en el núcleo radiactivo se produce una interacción magnética y eléctrica al mismo tiempo, como se ha descrito anteriormente, se obtienen interacciones combinadas. Esto conduce a la división de las frecuencias observadas en cada caso. El análisis puede no ser trivial debido al mayor número de frecuencias que deben asignarse. Estas dependen entonces en cada caso de la dirección del campo eléctrico y magnético entre sí en el cristal. El PAC es una de las pocas formas en que se pueden determinar estas direcciones.

Interacciones dinámicas

Si el campo hiperfino fluctúa durante la vida útil del nivel intermedio debido a saltos de la sonda a otra posición de la red o a saltos de un átomo cercano a otra posición de la red, se pierde la correlación. Para el caso simple con una red no distorsionada de simetría cúbica, para una tasa de salto de para lugares equivalentes , se observa una amortiguación exponencial de los términos estáticos: ${\displaystyle \tau _{n}}$ ${\displaystyle \omega _{s}<0.2\cdot \nu _{Q}}$ ${\displaystyle N_{s}}$ ${\displaystyle G_{22}(t)}$

${\displaystyle G_{22}^{dyn}(t)=e^{-\lambda _{d}t}G_{22}(t)}$             ${\displaystyle \lambda _{d}=(N_{s}-1)\omega _{s}}$

Aquí hay una constante a determinar, que no debe confundirse con la constante de decaimiento . Para valores grandes de , solo se puede observar un decaimiento exponencial puro: ${\displaystyle \lambda _{d}}$ ${\displaystyle \lambda ={\frac {1}{\tau }}}$ ${\displaystyle \omega _{s}}$

${\displaystyle G_{22}^{dyn}(t)=e^{-\lambda _{d}t}}$

El caso límite después de Abragam-Pound es , si , entonces: ${\displaystyle \lambda _{d}}$ ${\displaystyle \omega _{s}>3\cdot \nu _{Q}}$

${\displaystyle \lambda _{d}\approx {\frac {2,5\nu _{Q}^{2}}{N_{s}\omega _{s}}}}$

Efectos posteriores

Esquema de desintegración de ¹¹¹ In después de ¹¹¹ Cd, que ilustra las probabilidades de ocupación inicial entre un estado estático Cd ²⁺ y un estado dinámico altamente ionizado Cd ^x+ .

Los núcleos que se transmutan antes de la cascada - suelen provocar un cambio de carga en los cristales iónicos (In ³⁺ ) a Cd ²⁺ ). Como resultado, la red debe responder a estos cambios. Los defectos o iones vecinos también pueden migrar. Asimismo, el proceso de transición de alta energía puede provocar el efecto Auger , que puede llevar al núcleo a estados de ionización más altos. La normalización del estado de carga depende entonces de la conductividad del material. En los metales, el proceso se produce muy rápidamente. Esto lleva considerablemente más tiempo en semiconductores y aislantes. En todos estos procesos, el campo hiperfino cambia. Si este cambio se produce dentro de la cascada - , puede observarse como un efecto posterior. ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$

El número de núcleos en el estado (a) en la imagen de la derecha se despobla tanto por la desintegración después del estado (b) como después del estado (c):

${\displaystyle \mathrm {d} N_{a}=-N_{a}\left(\Gamma _{r}+{\frac {1}{\tau _{7/2}}}\right)\mathrm {d} t}$

con: ${\displaystyle \tau _{7/2}={\frac {120{\textrm {ps}}}{\ln {2}}}}$

De aquí se obtiene el caso exponencial:

${\displaystyle N_{a}(t)=N_{a_{0}}\cdot e^{\left({-(\Gamma _{r}+{\frac {1}{\tau _{7/2}}})t}\right)}}$

Para el número total de núcleos en el estado estático (c) se sigue:

${\displaystyle N_{c}(t)=\Gamma _{r}\int \limits _{0}^{t}N_{a}(t)\mathrm {d} t=N_{0}{\frac {\Gamma _{r}\tau _{7/2}}{\Gamma _{r}\tau _{7/2}+1}}\left(1-e^{-(\Gamma _{r}+{\frac {1}{\tau _{7/2}}})t}\right)}$

Las probabilidades de ocupación inicial son para entornos estáticos y dinámicos: ${\displaystyle \rho }$

${\displaystyle \rho _{stat}={\frac {\Gamma _{r}\tau _{7/2}}{\Gamma _{r}\tau _{7/2}+1}}}$

${\displaystyle \rho _{dyn}={\frac {1}{\Gamma _{r}\tau _{7/2}+1}}}$

Teoría general

Cascada general γ-γ con tiempo de vida del estado intermedio. ${\displaystyle \tau _{N}}$

En la teoría general para una transición se da: ${\displaystyle M_{i}\rightarrow M_{f}}$

${\displaystyle W(M_{i}\rightarrow M_{f})=\left|\sum _{M}\langle M_{f}|{\mathcal {H}}_{2}|M\rangle \langle M|{\mathcal {H}}_{1}|M_{i}\rangle \right|^{2}}$

${\displaystyle W({\vec {k}}_{1},{\vec {k}}_{2})=\sum _{M_{i},M_{f},\sigma _{1},\sigma _{2}}\left|\sum _{M}\langle M_{f}|{\mathcal {H}}_{2}|M\rangle \langle M|{\mathcal {H}}_{1}|M_{i}\rangle \right|^{2}}$

${\displaystyle W({\vec {k}}_{1},{\vec {k}}_{2})=W(\Theta )=\sum _{k_{gerade}}^{k_{max}}A_{k}(1)A_{k}(2)P_{k}(\cos {\Theta })}$

${\displaystyle 0\leq k\leq }$Mínimo de ${\displaystyle (2I,l_{1}+l_{1}',l_{2}+l_{2}')}$

Ángulos del detector

${\displaystyle W(\Theta ,t)=\sum _{k=2,4}A_{kk}P_{k}(\cos {\Theta })}$

${\displaystyle |M_{a}\rangle \rightarrow \Lambda (t)|M_{a}=\sum _{M_{b}}|M_{b}\rangle \langle M_{b}|\Lambda (t)|M_{a}\rangle }$

${\displaystyle W({\vec {k}}_{1},{\vec {k}}_{2},t)=\sum _{M_{i},M_{f},\sigma _{1},\sigma _{2}}\left|\sum _{M_{a}}\langle M_{f}|{\mathcal {H}}_{2}\Lambda (t)|M_{a}\rangle \langle M_{a}|{\mathcal {H}}_{1}|M_{i}\rangle \right|^{2}=\langle \rho ({\vec {k}}_{2})\rangle _{t}}$

${\displaystyle W({\vec {k}}_{1},{\vec {k}}_{2},t)=\sum _{k_{1},k_{2},N_{1},N_{2}}A_{k_{1}}(1)A_{k_{2}}(2){\frac {1}{\sqrt {(2k_{1}+1)(2k_{2}+1)}}}\times Y_{k_{1}}^{N_{1}}(\Theta _{1},\Phi _{1})\cdot Y_{k_{2}}^{N_{2}}(\Theta _{2},\Phi _{2})G_{k_{1}k_{2}}^{N_{1}N_{2}}(t)}$

con:

${\displaystyle G_{k_{1}k_{2}}^{N_{1}N_{2}}=\sum _{M_{a},M_{b}}(-1)^{2I+M_{a}+M_{b}}{\sqrt {(2k_{1}+1)(2k_{2}+)}}\times \langle M_{b}|\Lambda (t)|M_{a}\rangle \langle M_{b}'|\Lambda (t)|M_{a}'\rangle ^{*}\times {\begin{pmatrix}I&I&k_{1}\\M_{a}'&-M_{a}&N_{1}\end{pmatrix}}{\begin{pmatrix}I&I&k_{2}\\M_{b}'&-M_{b}&N_{2}\end{pmatrix}}}$

Referencias

1. Hamilton, Donald R. (15 de julio de 1940). "Sobre la correlación direccional de cuantos sucesivos". Physical Review . 58 (2). American Physical Society (APS): 122–131. Bibcode :1940PhRv...58..122H. doi :10.1103/physrev.58.122. ISSN  0031-899X.
2. Brady, Edward L.; Deutsch, Martin (1947-11-01). "Correlación angular de cuantos sucesivos de rayos gamma". Physical Review . 72 (9). American Physical Society (APS): 870–871. Bibcode :1947PhRv...72..870B. doi :10.1103/physrev.72.870. ISSN  0031-899X.
3. Aeppli, H.; Bishop, AS; Frauenfelder, H.; Walter, M.; Zünti, W. (15 de mayo de 1951). "Influencia de la capa atómica en la correlación angular nuclear en Cd ¹¹¹ ". Physical Review . 82 (4). American Physical Society (APS): 550. Bibcode :1951PhRv...82..550A. doi :10.1103/physrev.82.550. ISSN  0031-899X.
4. Gardner, JW (1949-12-01). "Correlación direccional entre electrones de conversión interna sucesivos". Actas de la Physical Society. Sección A . 62 (12). IOP Publishing: 763–779. Bibcode :1949PPSA...62..763G. doi :10.1088/0370-1298/62/12/302. ISSN  0370-1298.
5. Ling, Daniel S.; Falkoff, David L. (1949-12-01). "Efectos de interferencia en correlaciones angulares gamma-gamma". Physical Review . 76 (11). American Physical Society (APS): 1639–1648. Bibcode :1949PhRv...76.1639L. doi :10.1103/physrev.76.1639. ISSN  0031-899X.
6. Fierz, M. (1949). "Zur Theorie der Multipolstrahlung". Helvetica Physica Acta (en alemán). 22 (4): 489.
7. JA Spiers, Consejo Nacional de Res. de Canadá, Publ. No. 1925 (1950)
8. Spiers, JA (1950-11-01). "Sobre la correlación direccional de radiaciones nucleares sucesivas". Physical Review . 80 (3). American Physical Society (APS): 491. Bibcode :1950PhRv...80..491S. doi :10.1103/physrev.80.491. ISSN  0031-899X.
9. Falkoff, David L.; Uhlenbeck, GE (15 de julio de 1950). "Sobre la correlación direccional de radiaciones nucleares sucesivas". Physical Review . 79 (2). American Physical Society (APS): 323–333. Bibcode :1950PhRv...79..323F. doi :10.1103/physrev.79.323. ISSN  0031-899X.
10. Racah, Giulio (1951-12-01). "Correlación direccional de radiaciones nucleares sucesivas". Physical Review . 84 (5). American Physical Society (APS): 910–912. Bibcode :1951PhRv...84..910R. doi :10.1103/physrev.84.910. ISSN  0031-899X.
11. U. Fano, Informe 1214 de la Oficina Nacional de Normas
12. Fano, U. (15 de mayo de 1953). "Caracterización geométrica de los estados nucleares y la teoría de las correlaciones angulares". Physical Review . 90 (4). American Physical Society (APS): 577–579. Bibcode :1953PhRv...90..577F. doi :10.1103/physrev.90.577. ISSN  0031-899X.
13. Lloyd, Stuart P. (1 de marzo de 1952). "La correlación angular de dos radiaciones nucleares sucesivas". Physical Review . 85 (5). American Physical Society (APS): 904–911. Bibcode :1952PhRv...85..904L. doi :10.1103/physrev.85.904. ISSN  0031-899X.
14. Adler, K. (1952). "Beiträge zur Theorie der Richtungskorrelation". Helvetica Physica Acta (en alemán). 25 (3): 235.
15. De Groot, SR (1952). "Sobre las teorías de la distribución angular y la correlación de la radiación beta y gamma". Physica . 18 (12). Elsevier BV: 1201–1214. Bibcode :1952Phy....18.1201D. doi :10.1016/s0031-8914(52)80196-x. ISSN  0031-8914.
16. F. Coester, J. M. Jauch, Helv. Phys. Acta 26 (1953) 3.
17. Biedenharn, LC; Rose, ME (1 de julio de 1953). "Teoría de la correlación angular de las radiaciones nucleares". Reseñas de física moderna . 25 (3). Sociedad Estadounidense de Física (APS): 729–777. Código Bibliográfico :1953RvMP...25..729B. doi :10.1103/revmodphys.25.729. ISSN  0034-6861.
18. Abragam, A.; Pound, RV (15 de noviembre de 1953). "Influencia de los campos eléctricos y magnéticos en las correlaciones angulares". Physical Review . 92 (4). American Physical Society (APS): 943–962. Bibcode :1953PhRv...92..943A. doi :10.1103/physrev.92.943. ISSN  0031-899X.
19. Th. Wichert, E. Recknagel: Correlación angular perturbada. En: Ulrich Gonser (Ed.): Métodos microscópicos en metales (= Temas de la física actual. Banda 40). Springer, Berlín/Heidelberg 1986, ISBN 978-3-642-46571-0 , págs. 317–364, doi:10.1007/978-3-642-46571-0_11 
20. Collins, Gary S.; Shropshire, Steven L.; Fan, Jiawen (1990). "Correcciones angulares γ−γ perturbadas: una espectroscopia para defectos puntuales en metales y aleaciones". Interacciones hiperfinas . 62 (1–2). Springer Science and Business Media LLC: 1–34. doi :10.1007/bf02407659. ISSN  0304-3843. S2CID  94593348.
21. Th. Wichert, N. Achziger, H. Metzner, R. Sielemann: Correlación angular perturbada. En: G. Langouche (Ed.): Interacciones hiperfinas de defectos en semiconductores. Elsevier, Ámsterdam 1992, ISBN 0-444-89134-X , pág.77 
22. Jens Röder, Klaus-dieter Becker: Correlación angular γ-γ perturbada. En: Métodos en Química Física. John Wiley & Sons, Ltd, 2012, ISBN 978-3-527-32745-4 , págs. 325–349, doi:10.1002/9783527636839.ch10 
23. Günter Schatz, Alois Weidinger, Manfred Deicher: Nukleare Festkörperphysik: Kernphysikalische Messmethoden und ihre Anwendungen. 4. Auflaje. Vieweg+Teubner Verlag, 2010, ISBN 978-3-8351-0228-6 
24. Hemmingsen, Lars; Sas, Klára Nárcisz; Danielsen, Eva (2004). "Aplicaciones biológicas de las correlaciones angulares perturbadas de la espectroscopia de rayos gamma". Chemical Reviews . 104 (9). Sociedad Química Estadounidense (ACS): 4027–4062. doi :10.1021/cr030030v. ISSN  0009-2665. PMID  15352785.
25. Herden, C.; Röder, J.; Gardner, JA; Becker, KD (2008). "Espectrómetro de correlación angular perturbada diferencial de tiempo (TDPAC) totalmente digital". Instrumentos y métodos nucleares en la investigación en física Sección A: aceleradores, espectrómetros, detectores y equipos asociados . 594 (2). Elsevier BV: 155–161. Bibcode :2008NIMPA.594..155H. doi :10.1016/j.nima.2008.05.001. ISSN  0168-9002.
26. Nagl, Matías; Vetter, Ulrich; Uhrmacher, Michael; Hofsäss, Hans (2010). "Un nuevo espectrómetro de correlación angular diferencial de tiempo γ-γ totalmente digital". Revisión de Instrumentos Científicos . 81 (7). Publicación AIP: 073501–073501–9. Código Bib : 2010RScI...81g3501N. doi : 10.1063/1.3455186. ISSN  0034-6748. PMID  20687716.
27. Jäger, M.; Iwig, K.; Butz, T. (2010). "Un espectrómetro TDPAC totalmente digital y fácil de usar". Interacciones hiperfinas . 198 (1–3). Springer Science and Business Media LLC: 167–172. Bibcode :2010HyInt.198..167J. doi :10.1007/s10751-010-0201-8. ISSN  0304-3843. S2CID  17531166.