En matemáticas , la paradoja de Cramer o paradoja de Cramer-Euler [1] es la afirmación de que el número de puntos de intersección de dos curvas de orden superior en el plano puede ser mayor que el número de puntos arbitrarios que normalmente se necesitan para definir una de esas curvas. Recibe su nombre en honor al matemático ginebrino Gabriel Cramer .
Este fenómeno parece paradójico porque los puntos de intersección no definen de forma única ninguna curva (pertenecen al menos a dos curvas diferentes) a pesar de su gran número. Es el resultado de una comprensión ingenua o de una aplicación errónea de dos teoremas:
Para todos , , por lo que parecería ingenuamente que para el grado tres o superior, la intersección de dos curvas tendría suficientes puntos para definir cualquiera de las curvas de forma única. Sin embargo, debido a que estos puntos pertenecen a ambas curvas, no definen una curva única de este grado. La resolución de la paradoja es que el límite en el número de puntos necesarios para definir una curva solo se aplica a los puntos en la posición general . En ciertos casos degenerados , los puntos no son suficientes para determinar una curva de forma única.
La paradoja fue publicada por primera vez por Colin Maclaurin en 1720. [2] [3] Cramer y Leonhard Euler se escribieron sobre la paradoja en cartas de 1744 y 1745 y Euler le explicó el problema a Cramer. [4] Se la conoce como la paradoja de Cramer después de aparecer en su libro de 1750 Introduction à l'analyse des lignes courbes algébriques , aunque Cramer citó a Maclaurin como la fuente de la declaración. [5] Casi al mismo tiempo, Euler publicó ejemplos que mostraban una curva cúbica que no estaba definida únicamente por 9 puntos [4] [6] y discutió el problema en su libro Introductio in analysin infinitorum . El resultado fue publicado por James Stirling y explicado por Julius Plücker . [1]
En el caso de las curvas de primer orden (es decir, las rectas ) no se produce la paradoja, porque , por lo que . En general, dos rectas distintas se cortan en un único punto, a menos que las rectas tengan la misma pendiente, en cuyo caso no se cortan en absoluto. Un único punto no es suficiente para definir una recta (se necesitan dos); por el punto de intersección pasan no sólo las dos rectas dadas, sino también un número infinito de otras rectas.
Dos cónicas no degeneradas se cortan como máximo en cuatro puntos finitos del plano real, que es precisamente el número dado como máximo por el teorema de Bézout. Sin embargo, se necesitan cinco puntos para definir una cónica no degenerada, por lo que tampoco en este caso hay paradoja.

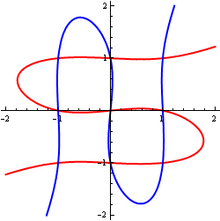
En una carta a Euler, Cramer señaló que las curvas cúbicas y se intersecan en exactamente nueve puntos. [ cita requerida ] La primera ecuación define tres líneas verticales , , y , y de manera similar, la segunda ecuación define tres líneas horizontales; estas líneas se intersecan en una cuadrícula de nueve puntos. Por lo tanto, nueve puntos no son suficientes para determinar de manera única una curva cúbica en casos degenerados como estos.
Una ecuación bivariada de grado n tiene 1 + n ( n + 3) / 2 coeficientes, pero el conjunto de puntos descritos por la ecuación se conserva si la ecuación se divide por uno de los coeficientes distintos de cero, dejando un coeficiente igual a 1 y solo n ( n + 3) / 2 coeficientes para caracterizar la curva. Dados n ( n + 3) / 2 puntos ( x i , y i ), cada uno de estos puntos se puede utilizar para crear una ecuación separada sustituyéndolo en la ecuación polinómica general de grado n , dando n ( n + 3) / 2 ecuaciones lineales en los n ( n + 3) / 2 coeficientes desconocidos. Si este sistema no es degenerado en el sentido de tener un determinante distinto de cero , los coeficientes desconocidos están determinados de forma única y, por lo tanto, la ecuación polinómica y su curva están determinadas de forma única. Pero si este determinante es cero, el sistema es degenerado y los puntos pueden estar en más de una curva de grado n .