Inclinación

Animación de nutación de una esfera

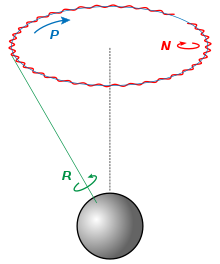
La nutación (del latín nūtātiō 'cabeceo, balanceo') es un movimiento de balanceo, balanceo o cabeceo en el eje de rotación de un objeto en gran medida simétrico axialmente, como un giroscopio , un planeta o una bala en vuelo , o como un comportamiento previsto de un mecanismo. En un marco de referencia apropiado, se puede definir como un cambio en el segundo ángulo de Euler . Si no es causado por fuerzas externas al cuerpo, se llama nutación libre o nutación de Euler . ^[1] Una nutación pura es un movimiento de un eje de rotación tal que el primer ángulo de Euler es constante. ^[^{cita requerida}^] Por lo tanto, se puede ver que la flecha roja circular en el diagrama indica los efectos combinados de la precesión y la nutación, mientras que la nutación en ausencia de precesión solo cambiaría la inclinación desde la vertical (segundo ángulo de Euler). Sin embargo, en la dinámica de las naves espaciales, la precesión (un cambio en el primer ángulo de Euler) a veces se denomina nutación. ^[2]

En un cuerpo rígido

Si se coloca una peonza inclinada sobre una superficie horizontal y se hace girar rápidamente, su eje de rotación comienza a realizar un movimiento de precesión alrededor de la vertical. Después de un breve intervalo, la peonza se asienta en un movimiento en el que cada punto de su eje de rotación sigue una trayectoria circular. La fuerza vertical de la gravedad produce un par horizontal $τ$ alrededor del punto de contacto con la superficie; la peonza gira en la dirección de este par con una velocidad angular $Ω$ tal que en cualquier momento

{\boldsymbol {\tau}}=\mathbf {\Omega} \times \mathbf {L} ,

( producto vectorial )

donde $L$ es el momento angular instantáneo del trompo. ^[3]

Sin embargo, al principio no hay precesión y la parte superior del trompo cae de lado y hacia abajo, inclinándose. Esto da lugar a un desequilibrio en los pares que inicia la precesión. Al caer, el trompo sobrepasa la cantidad de inclinación en la que precesaría de manera constante y luego oscila alrededor de este nivel. Esta oscilación se llama nutación . Si el movimiento se amortigua, las oscilaciones se reducirán hasta que el movimiento sea una precesión constante. ^[3]^[4]

La física de la nutación en peonzas y giroscopios se puede explorar utilizando el modelo de una peonza simétrica pesada con su punta fija. (Una peonza simétrica es una con simetría rotacional, o más generalmente una en la que dos de los tres momentos principales de inercia son iguales). Inicialmente, se ignora el efecto de la fricción. El movimiento de la peonza se puede describir mediante tres ángulos de Euler : el ángulo de inclinación $θ$ entre el eje de simetría de la peonza y la vertical (segundo ángulo de Euler); el acimut $φ$ de la peonza sobre la vertical (primer ángulo de Euler); y el ángulo de rotación $ψ$ de la peonza sobre su propio eje (tercer ángulo de Euler). Por lo tanto, la precesión es el cambio en $φ$ y la nutación es el cambio en $θ$ . ^[5]

Si el trompo tiene masa $M$ y su centro de masas está a una distancia $l$ del punto de pivote, su potencial gravitacional relativo al plano del soporte es

V=Mgl\cos(\theta).

En un sistema de coordenadas donde el eje $z$ es el eje de simetría, el trompo tiene velocidades angulares $ω 1, ω 2, ω 3$ y momentos de inercia $I 1, I 2, I 3$ respecto a los ejes $x, y$ y $z$ . Como estamos tomando un trompo simétrico, tenemos $I 1$ = $I 2$ . La energía cinética es

E_{\text{r}}={\frac {1}{2}}I_{1}\left(\omega _{1}^{2}+\omega _{2}^{2}\right)+{\frac {1}{2}}I_{3}\omega _{3}^{2}.

En términos de los ángulos de Euler, esto es

E_{\text{r}}={\frac {1}{2}}I_{1}({\dot {\theta }}^{2}+{\dot {\phi }}^{2}\sin ^{2}(\theta )\right)+{\frac {1}{2}}I_{3}({\dot {\psi }}+{\dot {\phi }}\cos(\theta )\right)^{2}.

Si se resuelven las ecuaciones de Euler-Lagrange para este sistema, se descubre que el movimiento depende de dos constantes $a$ y $b$ (cada una relacionada con una constante de movimiento ). La velocidad de precesión está relacionada con la inclinación por

{\dot {\phi }}={\frac {ba\cos(\theta )}{\sin ^{2}(\theta )}}.

La inclinación está determinada por una ecuación diferencial para $u = cos(θ)$ de la forma

{\dot {u}}^{2}=f(u)

donde $f$ es un polinomio cúbico que depende de los parámetros $a$ y $b$ , así como de constantes relacionadas con la energía y el par gravitacional. Las raíces de $f$ son los cosenos de los ángulos en los que la tasa de cambio de $θ$ es cero. Uno de ellos no está relacionado con un ángulo físico; los otros dos determinan los límites superior e inferior del ángulo de inclinación, entre los cuales oscila el giroscopio. ^[6]

Astronomía

La nutación de un planeta se produce porque los efectos gravitatorios de otros cuerpos hacen que la velocidad de su precesión axial varíe con el tiempo, de modo que la velocidad no es constante. El astrónomo inglés James Bradley descubrió la nutación del eje de la Tierra en 1728.

Tierra

La nutación cambia sutilmente la inclinación axial de la Tierra con respecto al plano eclíptico , desplazando los principales círculos de latitud que están definidos por la inclinación de la Tierra (los círculos tropicales y los círculos polares ).

En el caso de la Tierra, las principales fuentes de fuerza de marea son el Sol y la Luna , que cambian continuamente de ubicación entre sí y, por lo tanto, causan nutación en el eje de la Tierra. El componente más grande de la nutación de la Tierra tiene un período de 18,6 años, el mismo que el de la precesión de los nodos orbitales de la Luna . ^[1] Sin embargo, hay otros términos periódicos significativos que deben tenerse en cuenta dependiendo de la precisión deseada del resultado. Una descripción matemática (conjunto de ecuaciones) que representa la nutación se llama ^{[¿ por quién? ]} una "teoría de la nutación". ^{[ cita requerida ]} En la teoría, los parámetros se ajustan en un método más o menos ad hoc para obtener el mejor ajuste a los datos. La dinámica simple del cuerpo rígido no da la mejor teoría; uno tiene que tener en cuenta las deformaciones de la Tierra, incluida la inelasticidad del manto y los cambios en el límite núcleo-manto . ^[7]

El término principal de nutación se debe a la regresión de la línea nodal de la Luna y tiene el mismo período de 6798 días (18,61 años). Alcanza más o menos 17″ de longitud y 9,2″ de oblicuidad . ^[8] Todos los demás términos son mucho más pequeños; el siguiente más grande, con un período de 183 días (0,5 años), tiene amplitudes de 1,3″ y 0,6″ respectivamente. Los períodos de todos los términos mayores de 0,0001″ (aproximadamente con la mayor precisión que la tecnología disponible puede medir) se encuentran entre 5,5 y 6798 días; por alguna razón (como con los períodos de mareas oceánicas) parecen evitar el rango de 34,8 a 91 días, por lo que es habitual ^{[ ¿según quién? ]} dividir la nutación en términos de período largo y período corto. Los términos de largo período se calculan y se mencionan en los almanaques, mientras que la corrección adicional debida a los términos de corto período se suele tomar de una tabla. También se pueden calcular a partir del día juliano según la metodología IAU 2000B. ^[9]

En la cultura popular

En la película de catástrofe de 1961 El día que la Tierra se incendió , la detonación casi simultánea de dos superbombas de hidrógeno cerca de los polos provoca un cambio en la nutación de la Tierra, así como un desplazamiento de 11° en la inclinación axial y un cambio en la órbita de la Tierra alrededor del Sol.

En Star Trek: La Nueva Generación , el "ciclado" o "cambio" rápido de la "nutación del escudo" se menciona con frecuencia como un medio para retrasar al antagonista en sus esfuerzos por atravesar las defensas y saquear el Enterprise u otra nave espacial.

Véase también

Notas

^ ab Lowrie, William (2007). Fundamentos de geofísica (2.ª ed.). Cambridge [ua]: Cambridge University Press . págs. 58–59. ISBN 9780521675963.
^ Kasdin, N. Jeremy; Paley, Derek A. (2010). Dinámica de ingeniería: una introducción completa . Princeton, NJ: Princeton University Press . pp. 526–527. ISBN 9780691135373.
^ ab Feynman, Leighton & Sands 2011, págs. 20–7 ^{[, aclaración necesaria ],}
^ Goldstein 1980, pág. 220
^ Goldstein 1980, pág. 217
^ Goldstein 1980, págs. 213-217
^ "Resolución 83 sobre la teoría de la nutación terrestre no rígida". Servicio Internacional de Rotación de la Tierra y Sistemas de Referencia . Agencia Federal de Cartografía y Geodesia. 2 de abril de 2009. Consultado el 6 de agosto de 2012 .
^ "Conceptos básicos de los vuelos espaciales, capítulo 2". Laboratorio de Propulsión a Chorro /NASA. 28 de agosto de 2013. Consultado el 26 de marzo de 2015 .
^ "NeoProgrammics - Computaciones científicas".

Referencias

Las conferencias de física de Feynman, vol. I, cap. 20: Rotación en el espacio
Goldstein, Herbert (1980). Mecánica clásica (2.ª ed.). Reading, Mass.: Addison-Wesley Pub. Co. ISBN 0201029189.
Lambeck, Kurt (2005). La rotación variable de la Tierra: causas y consecuencias geofísicas (1.ª edición impresa digitalmente). Cambridge: Cambridge University Press . ISBN 9780521673303.
Munk, Walter H.; MacDonald, Gordon JF (1975). La rotación de la Tierra: una discusión geofísica . Reimpresión. con correcciones. Cambridge, Inglaterra: Cambridge University Press. ISBN 9780521207782.