Complejidad del circuito

Modelo de complejidad computacional

Ejemplo de circuito booleano. Los nodos son puertas AND , los nodos son puertas OR y los nodos son puertas NOT. ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle \neg }$

En informática teórica , la complejidad de circuitos es una rama de la teoría de la complejidad computacional en la que las funciones booleanas se clasifican según el tamaño o la profundidad de los circuitos booleanos que las calculan. Un concepto relacionado es la complejidad de circuitos de un lenguaje recursivo que se determina mediante una familia uniforme de circuitos (véase más abajo). ${\displaystyle C_{1},C_{2},\ldots }$

Demostrar límites inferiores para el tamaño de circuitos booleanos que calculan funciones booleanas explícitas es un enfoque popular para separar clases de complejidad. Por ejemplo, una clase de circuito destacada , P/poly, consiste en funciones booleanas computables por circuitos de tamaño polinomial. Demostrar eso separaría P y NP (ver a continuación). ${\displaystyle {\mathsf {NP}}\not \subseteq {\mathsf {P/poly}}}$

Las clases de complejidad definidas en términos de circuitos booleanos incluyen AC 0 , AC , TC 0 , NC 1 , NC y P/poly .

Tamaño y profundidad

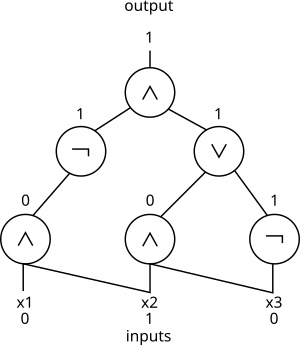
Un circuito booleano con bits de entrada es un gráfico acíclico dirigido en el que cada nodo (generalmente llamado compuerta en este contexto) es un nodo de entrada de grado de entrada 0 etiquetado por uno de los bits de entrada, una compuerta AND , una compuerta OR o una compuerta NOT . Una de estas compuertas se designa como la compuerta de salida. Un circuito de este tipo calcula naturalmente una función de sus entradas. El tamaño de un circuito es el número de compuertas que contiene y su profundidad es la longitud máxima de un camino desde una compuerta de entrada hasta la compuerta de salida. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Existen dos nociones principales de complejidad de circuitos ^[1] La complejidad del tamaño del circuito de una función booleana es el tamaño mínimo de cualquier circuito computacional . La complejidad de la profundidad del circuito de una función booleana es la profundidad mínima de cualquier circuito computacional . ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$

Estas nociones se generalizan cuando se considera la complejidad del circuito de cualquier lenguaje que contenga cadenas con diferentes longitudes de bits, especialmente lenguajes formales infinitos . Los circuitos booleanos, sin embargo, solo permiten un número fijo de bits de entrada. Por lo tanto, ningún circuito booleano es capaz de decidir tal lenguaje. Para tener en cuenta esta posibilidad, se consideran familias de circuitos donde cada uno acepta entradas de tamaño . Cada familia de circuitos generará naturalmente el lenguaje mediante la salida del circuito cuando una cadena de longitud es un miembro de la familia, y en caso contrario. Decimos que una familia de circuitos es de tamaño mínimo si no hay otra familia que decida sobre entradas de cualquier tamaño, , con un circuito de tamaño menor que (respectivamente para familias de profundidad mínima ). Por lo tanto, la complejidad del circuito es significativa incluso para lenguajes no recursivos . La noción de una familia uniforme permite que las variantes de la complejidad del circuito se relacionen con medidas de complejidad basadas en algoritmos de lenguajes recursivos. Sin embargo, la variante no uniforme es útil para encontrar límites inferiores sobre cuán compleja debe ser cualquier familia de circuitos para decidir lenguajes dados. ${\displaystyle C_{1},C_{2},\ldots }$ ${\displaystyle C_{n}}$ ${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle 1}$ ${\displaystyle n}$ ${\displaystyle 0}$ ${\displaystyle n}$ ${\displaystyle C_{n}}$

Por lo tanto, la complejidad del tamaño del circuito de un lenguaje formal se define como la función , que relaciona una longitud de bit de una entrada, , con la complejidad del tamaño del circuito de un circuito mínimo que decide si las entradas de esa longitud están en . La complejidad de la profundidad del circuito se define de manera similar. ${\displaystyle A}$ ${\displaystyle t:\mathbb {N} \to \mathbb {N} }$ ${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle A}$

Uniformidad

Los circuitos booleanos son uno de los principales ejemplos de los llamados modelos no uniformes de computación en el sentido de que las entradas de diferentes longitudes son procesadas por diferentes circuitos, en contraste con los modelos uniformes como las máquinas de Turing donde se utiliza el mismo dispositivo computacional para todas las longitudes de entrada posibles. Un problema computacional individual se asocia así con una familia particular de circuitos booleanos donde cada uno es el circuito que maneja entradas de n bits. A menudo se impone una condición de uniformidad en estas familias, requiriendo la existencia de alguna máquina de Turing posiblemente limitada por recursos que, en la entrada n , produzca una descripción del circuito individual . Cuando esta máquina de Turing tiene un polinomio de tiempo de ejecución en n , se dice que la familia de circuitos es P-uniforme. El requisito más estricto de DLOGTIME -uniformidad es de particular interés en el estudio de clases de circuitos de poca profundidad como AC ⁰ o TC ⁰ . Cuando no se especifican límites de recursos, un lenguaje es recursivo (es decir, decidible por una máquina de Turing) si y solo si el lenguaje es decidido por una familia uniforme de circuitos booleanos. ${\displaystyle C_{1},C_{2},\dots }$ ${\displaystyle C_{n}}$ ${\displaystyle C_{n}}$

Uniforme en tiempo polinomial

Una familia de circuitos booleanos es uniforme en tiempo polinomial si existe una máquina de Turing determinista M , tal que ${\displaystyle \{C_{n}:n\in \mathbb {N} \}}$

• M se ejecuta en tiempo polinomial
• Para todos , M genera una descripción de la entrada ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle C_{n}}$ ${\displaystyle 1^{n}}$

Uniforme del espacio logístico

Una familia de circuitos booleanos es uniforme en el espacio logarítmico si existe una máquina de Turing determinista M , tal que ${\displaystyle \{C_{n}:n\in \mathbb {N} \}}$

• M se ejecuta en un espacio de trabajo logarítmico (es decir, M es un transductor de espacio logarítmico )
• Para todos , M genera una descripción de la entrada ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle C_{n}}$ ${\displaystyle 1^{n}}$

Historia

La complejidad de los circuitos se remonta a Shannon en 1949 ^[2], quien demostró que casi todas las funciones booleanas con n variables requieren circuitos de tamaño Θ(2 ⁿ / n ). A pesar de este hecho, los teóricos de la complejidad hasta ahora no han podido demostrar un límite inferior superlineal para ninguna función explícita.

Los límites inferiores de los superpolinomios se han demostrado bajo ciertas restricciones en la familia de circuitos utilizados. La primera función para la que se mostraron límites inferiores de circuitos superpolinomios fue la función de paridad , que calcula la suma de sus bits de entrada módulo 2. El hecho de que la paridad no esté contenida en AC 0 fue establecido por primera vez de forma independiente por Ajtai en 1983 ^{[3] [4]} y por Furst, Saxe y Sipser en 1984. ^[5] Las mejoras posteriores de Håstad en 1987 ^[6] establecieron que cualquier familia de circuitos de profundidad constante que calcule la función de paridad requiere un tamaño exponencial. Extendiendo un resultado de Razborov, ^[7] Smolensky en 1987 ^[8] demostró que esto es cierto incluso si el circuito se amplía con puertas que calculan la suma de sus bits de entrada módulo algún primo impar p .

El problema de la k -clique consiste en decidir si un grafo dado en n vértices tiene una clique de tamaño k . Para cualquier elección particular de las constantes n y k , el grafo se puede codificar en binario utilizando bits, que indican para cada arista posible si está presente. Luego, el problema de la k -clique se formaliza como una función tal que da como salida 1 si y solo si el grafo codificado por la cadena contiene una clique de tamaño k . Esta familia de funciones es monótona y se puede calcular mediante una familia de circuitos, pero se ha demostrado que no se puede calcular mediante una familia de circuitos monótonos de tamaño polinomial (es decir, circuitos con puertas AND y OR pero sin negación). El resultado original de Razborov en 1985 ^[7] fue mejorado posteriormente a un límite inferior de tamaño exponencial por Alon y Boppana en 1987. ^[9] En 2008, Rossman ^[10] demostró que los circuitos de profundidad constante con puertas AND, OR y NOT requieren tamaño para resolver el problema de k -clique incluso en el caso promedio . Además, hay un circuito de tamaño que calcula . ${\displaystyle {n \choose 2}}$ ${\displaystyle f_{k}:\{0,1\}^{n \choose 2}\to \{0,1\}}$ ${\displaystyle f_{k}}$ ${\displaystyle \Omega (n^{k/4})}$ ${\displaystyle n^{k/4+O(1)}}$ ${\displaystyle f_{k}}$

En 1999, Raz y McKenzie demostraron posteriormente que la jerarquía NC monótona es infinita. ^[11]

El problema de división de enteros se encuentra en un TC uniforme de 0. ^[12]

Límites inferiores del circuito

Los límites inferiores del circuito son generalmente difíciles. Los resultados conocidos incluyen

• La paridad no existe en AC 0 no uniforme , como lo demostraron Ajtai en 1983 ^{[3] [4]} así como Furst, Saxe y Sipser en 1984. ^[5]
• El TC uniforme está estrictamente contenido en PP , como lo demostró Allender. ^[13]
• Las clases S^Pág.
  ₂, PP ^{[nb 1]} y MA /1 ^[14] (MA con un poco de consejo) no están en TAMAÑO ( n ^k ) para ninguna constante k.
• Si bien se sospecha que la clase no uniforme ACC ⁰ no contiene la función mayoritaria, recién en 2010 Williams demostró que . ^[15] ${\displaystyle {\mathsf {NEXP}}\not \subseteq {\mathsf {ACC}}^{0}}$

Está abierto si NEXPTIME tiene circuitos TC ⁰ no uniformes .

Las pruebas de los límites inferiores de los circuitos están estrechamente relacionadas con la desaleatorización . Una prueba que implicaría que uno o ambos permanentes no pueden calcularse mediante circuitos aritméticos no uniformes (polinomios) de tamaño y grado polinomiales. ^[16] ${\displaystyle {\mathsf {P}}={\mathsf {BPP}}}$ ${\displaystyle {\mathsf {NEXP}}\not \subseteq {\mathsf {P/poly}}}$

En 1997, Razborov y Rudich demostraron que muchos límites inferiores de circuitos conocidos para funciones booleanas explícitas implican la existencia de las llamadas propiedades naturales útiles contra la clase de circuito respectiva. ^[17] Por otro lado, las propiedades naturales útiles contra P/poly romperían los generadores pseudoaleatorios fuertes. Esto a menudo se interpreta como una barrera de "pruebas naturales" para demostrar límites inferiores de circuitos fuertes. En 2016, Carmosino, Impagliazzo, Kabanets y Kolokolova demostraron que las propiedades naturales también se pueden utilizar para construir algoritmos de aprendizaje eficientes. ^[18]

Clases de complejidad

Muchas clases de complejidad de circuitos se definen en términos de jerarquías de clases. Para cada entero no negativo i , existe una clase NC i , que consiste en circuitos de tamaño polinómico de profundidad , que utilizan puertas AND, OR y NOT acotadas en abanico . La unión NC de todas estas clases es un tema de discusión. Al considerar puertas fan-in ilimitadas, se pueden construir las clases AC i y AC (que es igual a NC). Se pueden construir muchas otras clases de complejidad de circuitos con las mismas restricciones de tamaño y profundidad al permitir diferentes conjuntos de puertas. ${\displaystyle O(\log ^{i}(n))}$

Relación con la complejidad del tiempo

Si un lenguaje determinado, pertenece a la clase de complejidad temporal para alguna función , entonces tiene complejidad de circuito . Si la máquina de Turing que acepta el lenguaje es inconsciente (es decir, lee y escribe las mismas celdas de memoria independientemente de la entrada), entonces tiene complejidad de circuito . ^[19] ${\displaystyle A}$ ${\displaystyle {\text{TIME}}(t(n))}$ ${\displaystyle t:\mathbb {N} \to \mathbb {N} }$ ${\displaystyle A}$ ${\displaystyle {\mathcal {O}}(t(n)\log t(n))}$ ${\displaystyle A}$ ${\displaystyle {\mathcal {O}}(t(n))}$

Circuitos monótonos

Un circuito booleano monótono es aquel que solo tiene puertas AND y OR, pero ninguna puerta NOT. Un circuito monótono solo puede calcular una función booleana monótona, que es una función donde para cada , , donde significa que para todos los . ${\displaystyle f:\{0,1\}^{n}\to \{0,1\}}$ ${\displaystyle x,y\in \{0,1\}^{n}}$ ${\displaystyle x\leq y\implies f(x)\leq f(y)}$ ${\displaystyle x\leq y}$ ${\displaystyle x_{i}\leq y_{i}}$ ${\displaystyle i\in \{1,\ldots ,n\}}$

Véase también

• Minimización de circuitos

Notas

1. Ver prueba .

Referencias

1. Sipser, Michael (1997). Introducción a la teoría de la computación (1.ª ed.). Boston, EE. UU.: PWS Publishing Company. pág. 324.
2. Shannon, Claude Elwood (1949). "La síntesis de circuitos de conmutación de dos terminales". Bell System Technical Journal . 28 (1): 59–98. doi :10.1002/j.1538-7305.1949.tb03624.x.
3. Ajtai, Miklós (1983). " -fórmulas sobre estructuras finitas". Anales de lógica pura y aplicada . 24 : 1–24. doi :10.1016/0168-0072(83)90038-6. ${\displaystyle \Sigma _{1}^{1}}$
4. Ajtai, Miklós ; Komlós, János ; Szemerédi, Endre (1983). "Una red de clasificación". Actas del 15º Simposio Anual de la ACM sobre Teoría de la Computación, 25 al 27 de abril de 1983, Boston, Massachusetts, EE. UU . Asociación de Maquinaria de Computación. págs. 1–9. doi :10.1145/800061.808726. ${\displaystyle O(n\log n)}$
5. Furst, Merrick L.; Saxe, James Benjamin ; Sipser, Michael Fredric (1984). "Paridad, circuitos y la jerarquía de tiempo polinomial". Teoría de sistemas matemáticos . 17 (1): 13–27. doi :10.1007/BF01744431. MR  0738749. S2CID  6306235.
6. Håstad, Johan Torkel (1987). Limitaciones computacionales de circuitos de pequeña profundidad (PDF) (tesis doctoral). Instituto Tecnológico de Massachusetts.
7. Razborov, Aleksandr Aleksandrovich (1985). "Límites inferiores de la complejidad monótona de algunas funciones booleanas". Matemáticas soviéticas - Doklady . 31 : 354–357. ISSN  0197-6788.
8. Smolensky, Roman (1987). "Métodos algebraicos en la teoría de límites inferiores para la complejidad de circuitos booleanos". Actas del 19.° Simposio Anual de la ACM sobre Teoría de la Computación . Association for Computing Machinery . págs. 77–82. doi : 10.1145/28395.28404 .
9. Alón, Noga ; Boppana, Ravi B. (1987). "La complejidad del circuito monótono de las funciones booleanas". Combinatoria . 7 (1): 1–22. CiteSeerX 10.1.1.300.9623 . doi :10.1007/bf02579196. S2CID  17397273. 
10. Rossman, Benjamin E. (2008). "Sobre la complejidad de profundidad constante de k-clique". STOC 2008: Actas del 40.º simposio anual de la ACM sobre teoría de la computación . Association for Computing Machinery . págs. 721–730. doi :10.1145/1374376.1374480.
11. Raz, Ran ; McKenzie, Pierre (1999). "Separación de la jerarquía NC monótona". Combinatorica . 19 (3): 403–435. doi :10.1007/s004930050062.
12. Hesse, William (2001). "La división está en uniforme TC ⁰ ". Actas del 28.º Coloquio Internacional sobre Autómatas, Lenguajes y Programación . Springer Verlag . pp. 104–114.
13. Allender, Eric (1996). "Complejidad de circuitos antes del amanecer del nuevo milenio". En Chandru, Vijay; Vinay, V. (eds.). Fundamentos de la tecnología de software y la ciencia informática teórica, 16.ª conferencia, Hyderabad, India, 18-20 de diciembre de 1996, Actas . Apuntes de clase en informática. Vol. 1180. Springer. págs. 1-18. doi :10.1007/3-540-62034-6_33.
14. Santhanam, Rahul (2007). "Circuit lower bounds for Merlin-Arthur classes" (Límites inferiores de circuitos para clases de Merlín-Arturo). STOC 2007: Actas del trigésimo noveno simposio anual de la ACM sobre teoría de la computación . págs. 275–283. CiteSeerX 10.1.1.92.4422 . doi :10.1145/1250790.1250832. 
15. Williams, Richard Ryan (2011). "Límites inferiores de circuitos ACC no uniformes" (PDF) . CCC 2011: Actas de la 26.ª Conferencia Anual del IEEE sobre Complejidad Computacional . págs. 115–125. doi :10.1109/CCC.2011.36.
16. Kabanets, Valentine; Impagliazzo, Russell Graham (2004). "Desaleatorizar las pruebas de identidad polinómica significa demostrar los límites inferiores del circuito". Complejidad computacional . 13 (1): 1–46. doi :10.1007/s00037-004-0182-6. S2CID  12451799.
17. Razborov, Aleksandr Aleksandrovich ; Rudich, Steven (1997). "Pruebas naturales". Revista de Ciencias de la Computación y de Sistemas . Vol. 55. págs. 24–35.
18. Carmosino, Marco; Impagliazzo, Russell Graham ; Kabanets, Valentine; Kolokolova, Antonina (2016). "Algoritmos de aprendizaje a partir de pruebas naturales". Computational Complexity Conference .
19. Pippenger, Nicholas ; Fischer, Michael J. (1979). "Relaciones entre medidas de complejidad". Revista de la ACM . 26 (3): 361–381. doi : 10.1145/322123.322138 . S2CID  2432526.

Lectura adicional

• Vollmer, Heribert [en alemán] (1999). Introducción a la complejidad de circuitos: un enfoque uniforme . Textos de informática teórica. Serie EATCS. ​​Springer Verlag . ISBN 978-3-540-64310-4.
• Wegener, Ingo (1987) [noviembre de 1986]. La complejidad de las funciones booleanas . Serie Wiley-Teubner en Ciencias de la Computación. Frankfurt am Main/Bielefeld, Alemania: John Wiley & Sons Ltd. y BG Teubner Verlag , Stuttgart. ISBN 3-519-02107-2. Código LCCN  87-10388.(xii+457 páginas) (NB: En su momento fue un influyente libro de texto sobre el tema, conocido comúnmente como el "Libro Azul". También disponible para descarga (PDF) en el Coloquio Electrónico sobre Complejidad Computacional .)
• Zwick, Uri . "Apuntes de clase para un curso de Uri Zwick sobre complejidad de circuitos".