Una señal multidimensional es una función de M variables independientes donde . Las señales del mundo real, que generalmente son señales de tiempo continuo, deben discretizarse (muestrearse) para garantizar que se puedan utilizar sistemas digitales para procesar las señales. Es durante este proceso de discretización donde el muestreo entra en escena. Aunque existen muchas formas de obtener una representación discreta de una señal de tiempo continuo, el muestreo periódico es, con mucho, el esquema más simple. Teóricamente, el muestreo se puede realizar con respecto a cualquier conjunto de puntos. Pero en la práctica, el muestreo se lleva a cabo con respecto a un conjunto de puntos que tienen una cierta estructura algebraica. Tales estructuras se denominan retículos . [1] Matemáticamente, el proceso de muestreo de una señal -dimensional se puede escribir como:
donde es un vector de dominio continuo de dimensión M (MD) que se está muestreando, es un vector entero de dimensión M correspondiente a los índices de una muestra, y V es una matriz de muestreo.
El muestreo multidimensional ofrece la oportunidad de analizar métodos digitales para procesar señales. Algunas de las ventajas de procesar señales en el dominio digital incluyen flexibilidad a través de operaciones DSP programables , almacenamiento de señales sin pérdida de fidelidad , posibilidad de cifrado en la comunicación y menor sensibilidad a las tolerancias del hardware. Por lo tanto, los métodos digitales son a la vez potentes y flexibles. En muchas aplicaciones, actúan como alternativas menos costosas que sus contrapartes analógicas. A veces, los algoritmos implementados utilizando hardware digital son tan complejos que no tienen contrapartes analógicas. El procesamiento de señales digitales multidimensionales se ocupa del procesamiento de señales representadas como matrices multidimensionales, como secuencias 2D o imágenes muestreadas.[1] El procesamiento de estas señales en el dominio digital permite el uso de hardware digital donde las operaciones de procesamiento de señales se especifican mediante algoritmos. Como las señales del mundo real son señales de tiempo continuo, el muestreo multidimensional juega un papel crucial en la discretización de las señales del mundo real. Las señales de tiempo discreto se procesan a su vez utilizando hardware digital para extraer información de la señal.
La región fuera de la cual las muestras de la señal toman valores cero se conoce como región de soporte (ROS). De la definición se desprende claramente que la región de soporte de una señal no es única.
La transformada de Fourier es una herramienta que nos permite simplificar las operaciones matemáticas que se realizan sobre la señal. La transformada básicamente representa cualquier señal como una combinación ponderada de senos . La transformada de Fourier y la transformada de Fourier inversa de una señal M-dimensional se pueden definir de la siguiente manera:
El símbolo de mayúscula ^ indica que la operación se realiza sobre vectores. Se observa que la transformada de Fourier de la señal muestreada es una extensión periódica de la transformada de Fourier de tiempo continuo de la señal. Esto se representa matemáticamente como:
De este modo, el muestreo en el dominio espacial da como resultado una periodicidad en el dominio de Fourier.

Una señal de banda limitada puede replicarse periódicamente de muchas maneras. Si la replicación da como resultado una superposición entre las regiones replicadas, la señal sufre aliasing . En tales condiciones, una señal de tiempo continuo no puede recuperarse perfectamente a partir de sus muestras. Por lo tanto, para garantizar la recuperación perfecta de la señal continua, debe haber un muestreo multidimensional de superposición cero de las regiones replicadas en el dominio transformado. Como en el caso de las señales unidimensionales, el aliasing se puede evitar si la señal de tiempo continuo se muestrea a una tasa suficientemente alta.
Es una medida del número de muestras por unidad de área. Se define como:
La cantidad mínima de muestras por unidad de área necesaria para recuperar por completo la señal de tiempo continuo se denomina densidad de muestreo óptima. En aplicaciones en las que la memoria o el tiempo de procesamiento son limitados, se debe hacer hincapié en minimizar la cantidad de muestras necesarias para representar la señal por completo.
En el caso de una forma de onda de banda limitada, existen infinitas formas de muestrear la señal sin producir alias en el dominio de Fourier, pero normalmente solo se utilizan dos estrategias: muestreo rectangular y muestreo hexagonal.

En el muestreo rectangular, una señal bidimensional, por ejemplo, se muestrea de acuerdo con la siguiente matriz V:
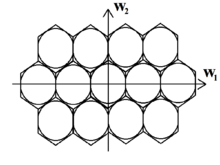
En el muestreo hexagonal, la matriz V asume la siguiente forma general:
La diferencia en la eficiencia de los dos esquemas se destaca utilizando una señal de banda limitada con una región circular de soporte de radio R. El círculo puede inscribirse en un cuadrado de longitud 2R o un hexágono regular de longitud . En consecuencia, la región de soporte ahora se transforma en un cuadrado y un hexágono respectivamente. Si estas regiones se replican periódicamente en el dominio de frecuencia de manera que no haya superposición entre dos regiones cualesquiera, entonces al replicar periódicamente la región cuadrada de soporte, muestreamos efectivamente la señal continua en una red rectangular. De manera similar, la replicación periódica de la región hexagonal de soporte se asigna al muestreo de la señal continua en una red hexagonal.
A partir de U, la matriz de periodicidad, podemos calcular la densidad de muestreo óptima tanto para los esquemas rectangulares como hexagonales. Se ha descubierto que, para recuperar por completo la señal circularmente limitada por la banda, el esquema de muestreo hexagonal requiere un 13,4% menos de muestras que el esquema de muestreo rectangular. La reducción puede parecer poco significativa para una señal bidimensional. Pero a medida que aumenta la dimensionalidad de la señal, la eficiencia del esquema de muestreo hexagonal se hará mucho más evidente. Por ejemplo, la reducción lograda para una señal de 8 dimensiones es del 93,8%. Para resaltar la importancia del resultado obtenido [2], intente visualizar una imagen como una colección de un número infinito de muestras. La entidad principal responsable de la visión, es decir, los fotorreceptores (bastones y conos) están presentes en la retina de todos los mamíferos. [3] Estas células no están dispuestas en filas y columnas. Al adaptar un esquema de muestreo hexagonal, nuestros ojos pueden procesar imágenes de manera mucho más eficiente. La importancia del muestreo hexagonal radica en el hecho de que los fotorreceptores del sistema de visión humano se encuentran en una red de muestreo hexagonal y, por lo tanto, realizan un muestreo hexagonal.[3] De hecho, se puede demostrar que el esquema de muestreo hexagonal es el esquema de muestreo óptimo para una señal de banda limitada circularmente. [4]
Los recientes avances en la tecnología CCD han hecho que el muestreo hexagonal sea factible para aplicaciones de la vida real. Históricamente, debido a las limitaciones tecnológicas, los conjuntos de detectores se implementaron solo en redes de muestreo rectangulares bidimensionales con detectores de forma rectangular. Pero el detector súper [CCD] introducido por Fuji tiene un píxel de forma octogonal en una cuadrícula hexagonal. Teóricamente, el rendimiento del detector aumentó en gran medida al introducir un píxel octogonal. Se redujo la cantidad de píxeles necesarios para representar la muestra y hubo una mejora significativa en la relación señal-ruido (SNR) en comparación con la de un píxel rectangular. [5] Pero el inconveniente de usar píxeles hexagonales es que el factor de relleno asociado será inferior al 82%. Un método alternativo sería interpolar píxeles hexagonales de tal manera que finalmente terminemos con una cuadrícula rectangular. El satélite Spot 5 incorpora una técnica similar donde dos CCD lineales idénticos transmiten dos imágenes casi idénticas que se desplazan medio píxel. Al interpolar las dos imágenes y procesarlas, se imita el funcionamiento de un detector con un píxel hexagonal.
Uno de los principales desafíos que se encuentran en el campo de los gráficos por computadora es representar la señal continua del mundo real como un conjunto discreto de puntos en la pantalla física. Se sabe desde hace mucho tiempo que las cuadrículas de muestreo hexagonales tienen varios beneficios en comparación con las cuadrículas rectangulares. Peterson y Middleton investigaron el muestreo y la reconstrucción de funciones M dimensionales limitadas por el número de onda y llegaron a la conclusión de que la red de muestreo óptima, en general, no es hexagonal. [6] Russell M. Mersereau desarrolló la transformada de Fourier discreta hexagonal ( DFT ) y los filtros de respuesta al impulso de extensión finita hexagonales. Pudo demostrar que para señales con banda limitada circularmente, el muestreo hexagonal es más eficiente que el muestreo rectangular. Cramblitt y Allebach desarrollaron métodos para diseñar patrones de muestreo secuencial temporal hexagonales óptimos y analizaron sus méritos en relación con los diseñados para una cuadrícula de muestreo rectangular. [7]

Una de las características únicas de una cuadrícula de muestreo hexagonal es que su transformada de Fourier sigue siendo hexagonal. También existe una relación inversa entre la distancia entre filas y columnas sucesivas (suponiendo que las muestras están ubicadas en el centro del hexágono). Esta relación inversa juega un papel muy importante en la minimización del aliasing y la maximización de la densidad mínima de muestreo. Es inevitable que exista un error de cuantificación al discretizar señales continuas del mundo real. Se han realizado experimentos para determinar qué configuración de detector producirá el menor error de cuantificación . Se descubrió que el muestreo espacial hexagonal producía el menor error de cuantificación para una resolución dada del sensor .
Conectividad consistente de cuadrículas hexagonales : En una cuadrícula hexagonal, podemos definir solo un fondo de 6 muestras de vecindad. Sin embargo, en una cuadrícula cuadrada, podemos definir un fondo de 4 u 8 muestras de vecindad (si se permite la conectividad diagonal). Debido a la ausencia de tal elección en cuadrículas hexagonales, se pueden diseñar algoritmos eficientes. La conectividad consistente también es responsable de una mejor resolución angular . Es por eso que la red hexagonal es mucho mejor para representar objetos curvos que la red rectangular. A pesar de estas varias ventajas, las cuadrículas hexagonales no se han utilizado prácticamente en la visión por computadora en su máximo potencial debido a la falta de hardware para procesar, capturar y mostrar imágenes basadas en hexágonos. Como se destacó anteriormente con el satélite Spot 5 , uno de los métodos que se están buscando para superar esta dificultad de hardware es imitar píxeles hexagonales utilizando píxeles cuadrados.