En geometría , la teselación triangular de orden 7 es una teselación regular del plano hiperbólico con un símbolo de Schläfli de {3,7}.
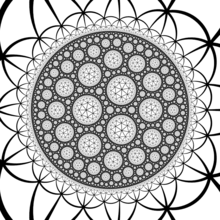
El grupo de simetría del teselado es el grupo de triángulos (2,3,7) y un dominio fundamental para esta acción es el triángulo de Schwarz (2,3,7) . Este es el triángulo de Schwarz hiperbólico más pequeño y, por lo tanto, por la prueba del teorema de automorfismos de Hurwitz , el teselado es el teselado universal que cubre todas las superficies de Hurwitz (las superficies de Riemann con grupo de simetría máximo), dándoles una triangulación cuyo grupo de simetría es igual a su grupo de automorfismos como superficies de Riemann.
La más pequeña de ellas es la superficie cuártica de Klein , la superficie de género 3 más simétrica, junto con un mosaico de 56 triángulos, que se encuentran en 24 vértices, con grupo de simetría el grupo simple de orden 168, conocido como PSL(2,7) . La superficie resultante puede a su vez sumergirse poliédricamente en el espacio euclidiano 3, produciendo el pequeño cuboctaedro cúbico . [1]
El mosaico heptagonal de orden 3 dual tiene el mismo grupo de simetría y, por lo tanto, produce mosaicos heptagonales de superficies de Hurwitz.
Está relacionado con dos teselaciones estelares por la misma disposición de vértices : la teselación heptagramática de orden 7 , {7/2,7}, y la teselación heptagonal de orden heptagramático , {7,7/2}.
Este mosaico está relacionado topológicamente como parte de una secuencia de poliedros regulares con el símbolo de Schläfli {3,p}.
Este mosaico es parte de la serie regular { n ,7}:
A partir de una construcción de Wythoff hay ocho teselaciones hiperbólicas uniformes que pueden basarse en la teselación heptagonal regular.
Dibujando las fichas coloreadas de rojo en las caras originales, amarillo en los vértices originales y azul a lo largo de los bordes originales, hay 8 formas.