Modulación por desplazamiento de amplitud

Esquema de modulación digital

La modulación por desplazamiento de amplitud ( ASK ) es una forma de modulación de amplitud que representa datos digitales como variaciones en la amplitud de una onda portadora . En un sistema ASK, se envía un símbolo , que representa uno o más bits , transmitiendo una onda portadora de amplitud fija a una frecuencia fija durante un período de tiempo específico. Por ejemplo, si cada símbolo representa un solo bit, la señal portadora podría transmitirse a una amplitud nominal cuando el valor de entrada es 1, pero a una amplitud reducida o no transmitirse en absoluto cuando el valor de entrada es 0.

Cualquier esquema de modulación digital utiliza un número finito de señales distintas para representar datos digitales. ASK utiliza un número finito de amplitudes, a cada una de las cuales se le asigna un patrón único de dígitos binarios . Por lo general, cada amplitud codifica un número igual de bits. Cada patrón de bits forma el símbolo que representa la amplitud particular. El demodulador , que está diseñado específicamente para el conjunto de símbolos utilizado por el modulador, determina la amplitud de la señal recibida y la asigna de nuevo al símbolo que representa, recuperando así los datos originales. La frecuencia y la fase de la portadora se mantienen constantes.

Al igual que la AM , una ASK también es lineal y sensible al ruido atmosférico, las distorsiones, las condiciones de propagación en diferentes rutas en PSTN , etc. Tanto los procesos de modulación como de demodulación ASK son relativamente económicos. La técnica ASK también se utiliza comúnmente para transmitir datos digitales a través de fibra óptica. Para los transmisores LED, el binario 1 se representa mediante un pulso corto de luz y el binario 0 mediante la ausencia de luz. Los transmisores láser normalmente tienen una corriente de "polarización" fija que hace que el dispositivo emita un nivel de luz bajo. Este nivel bajo representa el binario 0, mientras que una onda de luz de mayor amplitud representa el binario 1.

La forma más simple y común de ASK funciona como un conmutador, que utiliza la presencia de una onda portadora para indicar un uno binario y su ausencia para indicar un cero binario. Este tipo de modulación se denomina modulación de encendido y apagado (OOK) y se utiliza en frecuencias de radio para transmitir código Morse (lo que se conoce como operación de onda continua).

Se han desarrollado esquemas de codificación más sofisticados que representan datos en grupos utilizando niveles de amplitud adicionales. Por ejemplo, un esquema de codificación de cuatro niveles puede representar dos bits con cada desplazamiento de amplitud; un esquema de ocho niveles puede representar tres bits, y así sucesivamente. Estas formas de modulación por desplazamiento de amplitud requieren una alta relación señal/ruido para su recuperación, ya que por su naturaleza gran parte de la señal se transmite a potencia reducida.

Diagrama ASK

El sistema ASK se puede dividir en tres bloques. El primero representa el transmisor, el segundo es un modelo lineal de los efectos del canal y el tercero muestra la estructura del receptor. Se utiliza la siguiente notación:

• h _t (f) es la señal portadora para la transmisión
• h _c (f) es la respuesta al impulso del canal
• n (t) es el ruido introducido por el canal
• h _r (f) es el filtro en el receptor
• L es el número de niveles que se utilizan para la transmisión.
• T _s es el tiempo entre la generación de dos símbolos

Los distintos símbolos se representan con distintos voltajes. Si el valor máximo permitido para el voltaje es A, entonces todos los valores posibles están en el rango [−A, A] y se dan por:

${\displaystyle v_{i}={\frac {2A}{L-1}}i-A;\quad i=0,1,\dots ,L-1}$

La diferencia entre un voltaje y otro es:

${\displaystyle \Delta ={\frac {2A}{L-1}}}$

Considerando la imagen, los símbolos v[n] son ​​generados aleatoriamente por la fuente S, luego el generador de impulsos crea impulsos con un área de v[n]. Estos impulsos son enviados al filtro ht para ser enviados a través del canal. En otras palabras, para cada símbolo se envía una onda portadora diferente con la amplitud relativa.

Fuera del transmisor, la señal s(t) se puede expresar en la forma:

${\displaystyle s(t)=\sum _{n=-\infty }^{\infty }v[n]\cdot h_{t}(t-nT_{s})}$

En el receptor, después del filtrado a través de hr (t) la señal es:

${\displaystyle z(t)=n_{r}(t)+\sum _{n=-\infty }^{\infty }v[n]\cdot g(t-nT_{s})}$

donde utilizamos la notación:

${\displaystyle {\begin{aligned}n_{r}(t)&=n(t)*h_{r}(t)\\g(t)&=h_{t}(t)*h_{c}(t)*h_{r}(t)\end{aligned}}}$

donde * indica la convolución entre dos señales. Después de la conversión A/D, la señal z[k] se puede expresar de la siguiente forma:

${\displaystyle z[k]=n_{r}[k]+v[k]g[0]+\sum _{n\neq k}v[n]g[k-n]}$

En esta relación, el segundo término representa el símbolo que se debe extraer. Los demás son indeseados: el primero es el efecto del ruido, el tercero se debe a la interferencia entre símbolos.

Si los filtros se eligen de manera que g(t) satisfaga el criterio ISI de Nyquist, entonces no habrá interferencia entre símbolos y el valor de la suma será cero, por lo que:

${\displaystyle z[k]=n_{r}[k]+v[k]g[0]}$

La transmisión se verá afectada únicamente por el ruido.

Probabilidad de error

La función de densidad de probabilidad de tener un error de un tamaño determinado se puede modelar mediante una función gaussiana; el valor medio será el valor relativo enviado y su varianza estará dada por:

${\displaystyle \sigma _{N}^{2}=\int _{-\infty }^{+\infty }\Phi _{N}(f)\cdot |H_{r}(f)|^{2}df}$

donde es la densidad espectral del ruido dentro de la banda y Hr (f) es la transformada continua de Fourier de la respuesta al impulso del filtro hr (f). ${\displaystyle \Phi _{N}(f)}$

La probabilidad de cometer un error viene dada por:

${\displaystyle P_{e}=P_{e|H_{0}}\cdot P_{H_{0}}+P_{e|H_{1}}\cdot P_{H_{1}}+\cdots +P_{e|H_{L-1}}\cdot P_{H_{L-1}}=\sum _{k=0}^{L-1}P_{e|H_{k}}\cdot P_{H_{k}}}$

donde, por ejemplo, es la probabilidad condicional de cometer un error dado que se ha enviado un símbolo v0 y es la probabilidad de enviar un símbolo v0. ${\displaystyle P_{e|H_{0}}}$ ${\displaystyle P_{H_{0}}}$

Si la probabilidad de enviar cualquier símbolo es la misma, entonces:

${\displaystyle P_{H_{i}}={\frac {1}{L}}}$

Si representamos todas las funciones de densidad de probabilidad en la misma gráfica frente al valor posible del voltaje a transmitir, obtenemos una imagen como ésta ( se muestra el caso particular de): ${\displaystyle L=4}$

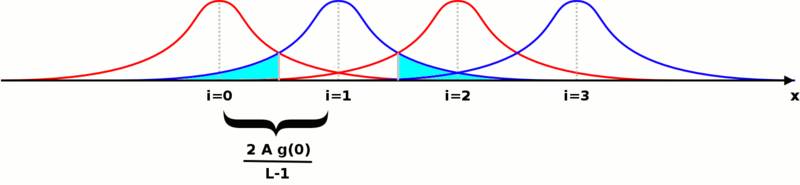
La probabilidad de cometer un error después de enviar un solo símbolo es el área de la función gaussiana que cae bajo las funciones de los otros símbolos. Se muestra en cian solo para uno de ellos. Si llamamos al área bajo un lado de la función gaussiana, la suma de todas las áreas será: . La probabilidad total de cometer un error se puede expresar en la forma: ${\displaystyle P^{+}}$ ${\displaystyle 2LP^{+}-2P^{+}}$

${\displaystyle P_{e}=2\left(1-{\frac {1}{L}}\right)P^{+}}$

Ahora tenemos que calcular el valor de . Para ello podemos mover el origen de la referencia a donde queramos: el área debajo de la función no cambiará. Nos encontramos en una situación como la que se muestra en la siguiente imagen: ${\displaystyle P^{+}}$

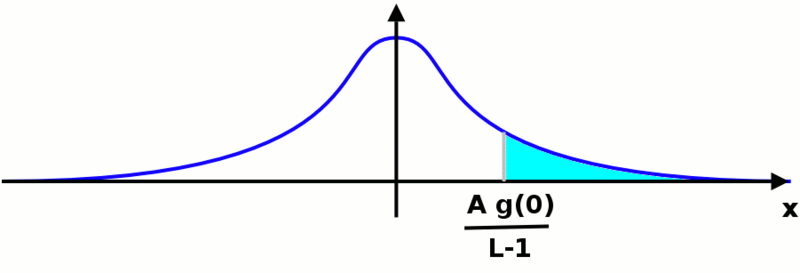
No importa qué función gaussiana estemos considerando, el área que queremos calcular será la misma. El valor que buscamos vendrá dado por la siguiente integral:

${\displaystyle P^{+}=\int _{\frac {Ag(0)}{L-1}}^{\infty }{\frac {1}{{\sqrt {2\pi }}\sigma _{N}}}e^{-{\frac {x^{2}}{2\sigma _{N}^{2}}}}dx={\frac {1}{2}}\operatorname {erfc} \left({\frac {Ag(0)}{{\sqrt {2}}(L-1)\sigma _{N}}}\right)}$

donde es la función de error complementaria. Al sumar todos estos resultados, la probabilidad de cometer un error es: ${\displaystyle \operatorname {erfc} (x)}$

${\displaystyle P_{e}=\left(1-{\frac {1}{L}}\right)\operatorname {erfc} \left({\frac {Ag(0)}{{\sqrt {2}}(L-1)\sigma _{N}}}\right)}$

De esta fórmula podemos entender fácilmente que la probabilidad de cometer un error disminuye si la amplitud máxima de la señal transmitida o la amplificación del sistema se hace mayor; por el contrario, aumenta si el número de niveles o la potencia del ruido se hace mayor.

Esta relación es válida cuando no hay interferencia entre símbolos, es decir, es una función de Nyquist . ${\displaystyle g(t)}$

Véase también

• Modulación por desplazamiento de frecuencia (FSK)

Enlaces externos

• Cálculo de la sensibilidad de un receptor con modulación por desplazamiento de amplitud (ASK) Archivado el 29 de agosto de 2009 en Wayback Machine