medoide

Los medoides son objetos representativos de un conjunto de datos o un grupo dentro de un conjunto de datos cuya suma de diferencias con todos los objetos del grupo es mínima. ^[1] Los medoides son similares en concepto a las medias o centroides , pero los medoides siempre están restringidos a ser miembros del conjunto de datos. Los medoides se utilizan más comúnmente en datos cuando no se puede definir una media o un centroide, como en gráficos. También se utilizan en contextos donde el centroide no es representativo del conjunto de datos, como en imágenes, trayectorias 3D y expresión genética ^[2] (donde, si bien los datos son escasos, el medoide no necesita serlo). Estos también son de interés cuando se desea encontrar un representante utilizando alguna distancia distinta a la distancia euclidiana al cuadrado (por ejemplo, en las clasificaciones de películas).

En algunos conjuntos de datos puede haber más de un medoide, como en el caso de las medianas. Una aplicación común del medoide es el algoritmo de agrupamiento de k-medoides , que es similar al algoritmo de k-medias , pero funciona cuando no se puede definir una media o un centroide. Este algoritmo funciona básicamente de la siguiente manera. En primer lugar, se elige un conjunto de medoides al azar. En segundo lugar, se calculan las distancias a los demás puntos. En tercer lugar, los datos se agrupan según el medoide al que son más similares. En cuarto lugar, el conjunto de medoides se optimiza mediante un proceso iterativo.

Tenga en cuenta que un medoide no es equivalente a una mediana , una mediana geométrica o un centroide . Una mediana solo se define en datos unidimensionales y solo minimiza la disimilitud con otros puntos para métricas inducidas por una norma (como la distancia de Manhattan o la distancia euclidiana ). Una mediana geométrica se define en cualquier dimensión, pero a diferencia de un medoide, no es necesariamente un punto dentro del conjunto de datos original.

Definición

Sea un conjunto de puntos en un espacio con una función de distancia d. El medoide se define como ${\textstyle {\mathcal {X}}:=\{x_{1},x_{2},\dots ,x_{n}\}}$ ${\textstyle n}$

${\displaystyle x_{\text{medoid}}=\arg \min _{y\in {\mathcal {X}}}\sum _{i=1}^{n}d(y,x_{i}).}$

Agrupamiento con medoides

Los medoides son un reemplazo popular para la media del grupo cuando la función de distancia no es la distancia euclidiana (al cuadrado) o ni siquiera una métrica (ya que el medoide no requiere la desigualdad triangular). Al dividir el conjunto de datos en grupos, el medoide de cada grupo se puede utilizar como representante de cada grupo.

Los algoritmos de agrupamiento basados ​​en la idea de medoides incluyen:

• Partitioning Around Medoids (PAM), el algoritmo k-medoids estándar
• Agrupamiento jerárquico alrededor de medoides (HACAM), que utiliza medoides en el agrupamiento jerárquico

Algoritmos para calcular el medoide de un conjunto

De la definición anterior, se desprende claramente que el medoide de un conjunto se puede calcular después de calcular todas las distancias por pares entre los puntos del conjunto. Esto requeriría evaluaciones de distancia (con ). En el peor de los casos, no se puede calcular el medoide con menos evaluaciones de distancia. ^{[3] [4]} Sin embargo, existen muchos enfoques que nos permiten calcular medoides de forma exacta o aproximada en tiempo subcuadrático bajo diferentes modelos estadísticos. ${\displaystyle {\mathcal {X}}}$ ${\textstyle O(n^{2})}$ ${\displaystyle n=|{\mathcal {X}}|}$

Si los puntos se encuentran en la línea real, el cálculo del medoide se reduce al cálculo de la mediana, que se puede realizar mediante el algoritmo de selección rápida de Hoare. ^[5] Sin embargo, en espacios reales de dimensión superior, no se conoce ningún algoritmo de tiempo lineal. RAND ^[6] es un algoritmo que estima la distancia promedio de cada punto a todos los demás puntos mediante el muestreo de un subconjunto aleatorio de otros puntos. Se necesitan un total de cálculos de distancia para aproximar el medoide dentro de un factor de con alta probabilidad, donde es la distancia máxima entre dos puntos en el conjunto. Tenga en cuenta que RAND es un algoritmo de aproximación y, además, puede que no se conozca a priori. ${\textstyle O(n)}$ ${\textstyle O\left({\frac {n\log n}{\epsilon ^{2}}}\right)}$ ${\textstyle (1+\epsilon \Delta )}$ ${\textstyle \Delta }$ ${\textstyle \Delta }$

RAND fue aprovechado por TOPRANK ^[7] , que utiliza las estimaciones obtenidas por RAND para centrarse en un pequeño subconjunto de puntos candidatos, evalúa la distancia promedio de estos puntos exactamente y elige el mínimo de ellos. TOPRANK necesita cálculos de distancia para encontrar el medoide exacto con alta probabilidad bajo un supuesto distribucional sobre las distancias promedio. ${\textstyle O(n^{\frac {5}{3}}\log ^{\frac {4}{3}}n)}$

trimed ^[3] presenta un algoritmo para encontrar el medoide con evaluaciones de distancia bajo un supuesto de distribución de los puntos. El algoritmo utiliza la desigualdad triangular para reducir el espacio de búsqueda. ${\textstyle O(n^{\frac {3}{2}}2^{\Theta (d)})}$

Meddit ^[4] aprovecha una conexión del cálculo de medoide con bandidos multiarmados y utiliza un tipo de algoritmo de límite de confianza superior para obtener un algoritmo que realiza evaluaciones de distancia bajo supuestos estadísticos sobre los puntos. ${\textstyle O(n\log n)}$

El halving secuencial correlacionado ^[8] también aprovecha las técnicas de multi-armed bandit, mejorando Meddit . Al explotar la estructura de correlación en el problema, el algoritmo puede producir una mejora drástica (generalmente alrededor de 1-2 órdenes de magnitud) tanto en la cantidad de cálculos de distancia necesarios como en el tiempo de reloj de pared.

Implementaciones

Aquí se puede encontrar una implementación de RAND , TOPRANK y trimed . Aquí y aquí se puede encontrar una implementación de Meddit . Aquí se puede encontrar una implementación de la reducción secuencial correlacionada .

Medoides en el procesamiento de texto y lenguaje natural (PLN)

Los medoides se pueden aplicar a varias tareas de texto y PNL para mejorar la eficiencia y precisión de los análisis. ^[9] Al agrupar datos de texto en función de la similitud, los medoides pueden ayudar a identificar ejemplos representativos dentro del conjunto de datos, lo que conduce a una mejor comprensión e interpretación de los datos.

Agrupamiento de texto

La agrupación de texto es el proceso de agrupar textos o documentos similares en función de su contenido. Los algoritmos de agrupación basados ​​en medoides se pueden emplear para dividir grandes cantidades de texto en grupos, cada uno de los cuales está representado por un documento medoide. Esta técnica ayuda a organizar, resumir y recuperar información de grandes colecciones de documentos, como en motores de búsqueda, análisis de redes sociales y sistemas de recomendación. ^[10]

Resumen de texto

El resumen de texto tiene como objetivo producir un resumen conciso y coherente de un texto más extenso extrayendo la información más importante y relevante. La agrupación basada en medoides se puede utilizar para identificar las oraciones más representativas de un documento o un grupo de documentos, que luego se pueden combinar para crear un resumen. Este enfoque es especialmente útil para tareas de resumen extractivo, donde el objetivo es generar un resumen seleccionando las oraciones más relevantes del texto original. ^[11]

Análisis de sentimientos

El análisis de sentimientos implica determinar el sentimiento o la emoción expresados ​​en un fragmento de texto, como positivo, negativo o neutral. La agrupación basada en medoides se puede aplicar para agrupar datos de texto en función de patrones de sentimientos similares. Al analizar el medoide de cada grupo, los investigadores pueden obtener información sobre el sentimiento predominante del grupo, lo que ayuda en tareas como la minería de opiniones, el análisis de los comentarios de los clientes y el seguimiento de las redes sociales. ^[12]

Modelado de temas

El modelado de temas es una técnica que se utiliza para descubrir temas abstractos que aparecen en una colección de documentos. La agrupación basada en medoides se puede aplicar para agrupar documentos con temas o temas similares. Al analizar los medoides de estos grupos, los investigadores pueden comprender los temas subyacentes en el corpus de texto, lo que facilita tareas como la categorización de documentos, el análisis de tendencias y la recomendación de contenido. ^[13]

Técnicas para medir la similitud de textos en agrupamientos basados ​​en medoides

Al aplicar la agrupación basada en medoides a los datos de texto, es esencial elegir una medida de similitud adecuada para comparar documentos de manera eficaz. Cada técnica tiene sus ventajas y limitaciones, y la elección de la medida de similitud debe basarse en los requisitos y características específicos de los datos de texto que se analizan. ^[14] Las siguientes son técnicas comunes para medir la similitud de texto en la agrupación basada en medoides:

Este ejemplo muestra cómo la similitud de coseno comparará el ángulo de las líneas entre objetos para determinar cuán similares son los elementos. Tenga en cuenta que la mayoría de las incrustaciones de texto tendrán al menos unos cientos de dimensiones en lugar de solo dos.

Semejanza de coseno

La similitud de coseno es una medida ampliamente utilizada para comparar la similitud entre dos fragmentos de texto. Calcula el coseno del ángulo entre dos vectores de documento en un espacio de alta dimensión. ^[14] La similitud de coseno varía entre -1 y 1, donde un valor más cercano a 1 indica una mayor similitud y un valor más cercano a -1 indica una menor similitud. Al visualizar dos líneas que se originan en el origen y se extienden hasta los respectivos puntos de interés, y luego medir el ángulo entre estas líneas, se puede determinar la similitud entre los puntos asociados. La similitud de coseno se ve menos afectada por la longitud del documento, por lo que puede ser mejor para producir medoides que sean representativos del contenido de un grupo en lugar de la longitud.

Similitud de Jaccard

Esta fórmula de similitud de Jaccard se puede aplicar fácilmente al texto.

La similitud de Jaccard, también conocida como coeficiente de Jaccard, mide la similitud entre dos conjuntos comparando la relación entre su intersección y su unión. En el contexto de los datos de texto, cada documento se representa como un conjunto de palabras y la similitud de Jaccard se calcula en función de las palabras comunes entre los dos conjuntos. La similitud de Jaccard varía entre 0 y 1, donde un valor más alto indica un mayor grado de similitud entre los documentos. ^{[ cita requerida ]}

Distancia euclidiana

Este ejemplo muestra cómo la distancia euclidiana calculará la distancia entre objetos para determinar cuán similares son. Tenga en cuenta que la mayoría de las incrustaciones de texto tendrán al menos unos cientos de dimensiones en lugar de solo dos.

La distancia euclidiana es una métrica de distancia estándar que se utiliza para medir la disimilitud entre dos puntos en un espacio multidimensional. En el contexto de los datos de texto, los documentos suelen representarse como vectores de alta dimensión, como los vectores TF, y la distancia euclidiana se puede utilizar para medir la disimilitud entre ellos. Una distancia euclidiana menor indica un mayor grado de similitud entre los documentos. ^[14] El uso de la distancia euclidiana puede dar como resultado medoides que sean más representativos de la longitud de un documento.

Editar distancia

La distancia de edición, también conocida como distancia de Levenshtein, mide la similitud entre dos cadenas calculando el número mínimo de operaciones (inserciones, eliminaciones o sustituciones) necesarias para transformar una cadena en otra. En el contexto de los datos de texto, la distancia de edición se puede utilizar para comparar la similitud entre documentos de texto cortos o palabras individuales. Una distancia de edición menor indica un mayor grado de similitud entre las cadenas. ^[15]

Aplicaciones de medoides en modelos de lenguaje de gran tamaño

Medoids para analizar incrustaciones de modelos de lenguaje de gran tamaño

Este es un ejemplo de cómo se puede agrupar el texto con elementos similares cuando se lo integra en función de la ubicación. Esto representa la agrupación por distancia euclidiana. Si se agruparan por una medida de similitud diferente, como la similitud del coseno, los medoides podrían ser diferentes.

Los medoides se pueden emplear para analizar y comprender las representaciones de espacios vectoriales generadas por modelos de lenguaje grandes (LLM), como BERT, GPT o RoBERTa. Al aplicar la agrupación basada en medoides a las incrustaciones producidas por estos modelos para palabras, frases u oraciones, los investigadores pueden explorar las relaciones semánticas capturadas por los LLM. Este enfoque puede ayudar a identificar agrupaciones de entidades semánticamente similares, lo que proporciona información sobre la estructura y la organización de los espacios de incrustación de alta dimensión generados por estos modelos. ^[16]

Medoides para selección de datos y aprendizaje activo

El aprendizaje activo implica la selección de puntos de datos de un conjunto de entrenamiento que maximizará el rendimiento del modelo. Los medoides pueden desempeñar un papel crucial en la selección de datos y el aprendizaje activo con los modelos de aprendizaje lineal. La agrupación basada en medoides se puede utilizar para identificar muestras representativas y diversas de un gran conjunto de datos de texto, que luego se pueden emplear para ajustar los modelos de aprendizaje lineal de manera más eficiente o para crear mejores conjuntos de entrenamiento. Al seleccionar medoides como ejemplos de entrenamiento, los investigadores pueden tener un conjunto de entrenamiento más equilibrado e informativo, lo que potencialmente mejora la generalización y la solidez de los modelos ajustados. ^[17]

Medoides para la interpretabilidad y seguridad de los modelos

La aplicación de medoides en el contexto de los LLM puede contribuir a mejorar la interpretabilidad del modelo. Al agrupar las incrustaciones generadas por los LLM y seleccionar medoides como representantes de cada grupo, los investigadores pueden proporcionar un resumen más interpretable del comportamiento del modelo. ^[18] Este enfoque puede ayudar a comprender el proceso de toma de decisiones del modelo, identificar posibles sesgos y descubrir la estructura subyacente de las incrustaciones generadas por los LLM. A medida que el debate sobre la interpretabilidad y la seguridad de los LLM continúa aumentando, el uso de medoides puede servir como una herramienta valiosa para lograr este objetivo.

Aplicaciones en el mundo real

Como método de agrupamiento versátil, los medoides se pueden aplicar a una variedad de problemas del mundo real en numerosos campos, que abarcan desde la biología y la medicina hasta la publicidad y el marketing y las redes sociales. Su potencial para manejar conjuntos de datos complejos con un alto grado de perplejidad lo convierte en una herramienta poderosa en el análisis de datos moderno.

Análisis de la expresión genética

En el análisis de la expresión génica, ^[19] los investigadores utilizan tecnologías avanzadas que consisten en microarrays y secuenciación de ARN para medir los niveles de expresión de numerosos genes en muestras biológicas, lo que da como resultado datos multidimensionales que pueden ser complejos y difíciles de analizar. Los medoides son una posible solución al agrupar genes principalmente en función de sus perfiles de expresión, lo que permite a los investigadores descubrir grupos de genes coexpresados ​​que podrían proporcionar información valiosa sobre los mecanismos moleculares de los procesos biológicos y las enfermedades.

Análisis de redes sociales

Para la evaluación de redes sociales, ^[20] los medoides pueden ser una herramienta excepcional para reconocer nodos centrales o influyentes en una red social. Los investigadores pueden agrupar nodos en función de sus estilos de conectividad e identificar los nodos que tienen más probabilidades de tener un impacto sustancial en la función y la estructura de la red. Un enfoque popular para hacer uso de los medoides en el análisis de redes sociales es calcular una métrica de distancia o similitud entre pares de nodos en función de sus propiedades.

Segmentación del mercado

Los medoides también se pueden utilizar para la segmentación del mercado, ^[21] que es un procedimiento analítico que incluye la agrupación de clientes principalmente en función de su comportamiento de compra, rasgos demográficos y otros atributos. La agrupación de clientes en segmentos mediante medoides permite a las empresas adaptar sus técnicas de publicidad y marketing de una manera que se alinee con las necesidades de cada grupo de clientes. Los medoides sirven como factores representativos dentro de cada grupo, encapsulando las características principales de los clientes en ese grupo.

La suma de errores al cuadrado dentro de los grupos (WGSS, por sus siglas en inglés) es una fórmula que se emplea en la segmentación de mercados y que tiene como objetivo cuantificar la concentración de errores al cuadrado dentro de los conglomerados. Busca capturar la distribución de errores dentro de los grupos elevándolos al cuadrado y agregando los resultados. La métrica WGSS cuantifica la cohesión de las muestras dentro de los conglomerados, lo que indica conglomerados más compactos con valores WGSS más bajos y un efecto de agrupamiento correspondientemente superior. La fórmula para WGSS es:

$${\displaystyle {\text{WGSS}}={\frac {1}{2}}\left[(m_{1}-1){\overline {d_{1}^{2}}}+\cdots +(m_{k}-1){\overline {d_{k}^{2}}}\right]}$$

Donde es la distancia promedio de las muestras dentro del k -ésimo grupo y es el número de muestras en el k -ésimo grupo. ${\displaystyle {\overline {d_{1}^{2}}}}$ ${\displaystyle m_{k}}$

Detección de anomalías

Los medoides también pueden ser útiles para identificar anomalías, y un método eficiente es la detección de anomalías basada en grupos. Se pueden utilizar para descubrir grupos de puntos de datos que se desvían significativamente del resto de los datos. Al agrupar los datos en grupos utilizando medoides y comparar las propiedades de cada grupo con los datos, los investigadores pueden detectar claramente los grupos que son anómalos. ^{[ cita requerida ]}

Visualización del proceso de agrupamiento basado en medoides

Objetivo

La visualización de la agrupación basada en medoides puede ser útil para intentar comprender cómo funciona la agrupación basada en medoides. Los estudios han demostrado que las personas aprenden mejor con información visual. ^[22] En la agrupación basada en medoides, el medoide es el centro del grupo. Esto es diferente de la agrupación de k-medias , donde el centro no es un punto de datos real, sino que puede estar entre puntos de datos. Usamos el medoide para agrupar "grupos" de datos, lo que se obtiene al encontrar el elemento con una disimilitud promedio mínima con todos los demás objetos en el grupo. ^[23]　Aunque el ejemplo de visualización utilizado utiliza la agrupación de k-medoides, la visualización también se puede aplicar a la agrupación de k-medias intercambiando la disimilitud promedio con la media del conjunto de datos que se está utilizando.

Visualización utilizando datos unidimensionales

Matriz de distancia

Ejemplo de un gráfico de disimilitud de Jaccard normalizado utilizando perfiles nucleares. Cada NP se compara con cada uno de los otros NP de la tabla y la disimilitud correspondiente se ingresa en la celda correspondiente al par de NP que se compara. Los números más altos indican una mayor disimilitud, mientras que los números más bajos indican una mayor similitud. La mayoría de las etiquetas se excluyen debido a restricciones de tamaño. La diagonal se marca como “0” para no sesgar los datos.

Se requiere una matriz de distancia para la agrupación basada en medoides, que se genera utilizando la disimilitud de Jaccard (que es 1 - el índice de Jaccard ). Esta matriz de distancia se utiliza para calcular la distancia entre dos puntos en un gráfico unidimensional. ^{[ cita requerida ]} La imagen anterior muestra un ejemplo de un gráfico de disimilitud de Jaccard.

Agrupamiento

Paso 1

La agrupación basada en medoides se utiliza para encontrar grupos dentro de un conjunto de datos. Para el proceso de agrupación basada en medoides se utiliza un conjunto de datos unidimensional inicial que contiene grupos que se deben descubrir. En la imagen siguiente, hay doce objetos diferentes en el conjunto de datos en distintas posiciones x.

El conjunto de datos inicial que se utilizará en esta sección. Un punto gris indica un objeto que no está asignado a ningún grupo.

Paso 2

Se eligen K puntos aleatorios como centros iniciales. El valor elegido para K se conoce como valor K. En la imagen siguiente, se ha elegido 3 como valor K. El proceso para encontrar el valor K óptimo se analizará en el paso 7.

La primera selección central. Los puntos grandes son los centros y los colores separan cada objeto por su grupo.

Paso 3

Cada objeto que no está en el centro se asigna a su centro más cercano. Esto se hace mediante una matriz de distancias. Cuanto menor sea la disimilitud, más cerca estarán los puntos. En la imagen siguiente, hay 5 objetos en el grupo 1, 3 en el grupo 2 y 4 en el grupo 3.

Los clusters iniciales.

Paso 4

El nuevo centro de cada grupo se determina buscando el objeto cuya disimilitud promedio con respecto a todos los demás objetos del grupo sea mínima. El centro seleccionado durante este paso se denomina medoide. La siguiente imagen muestra los resultados de la selección del medoide.

La selección medoide.

Paso 5

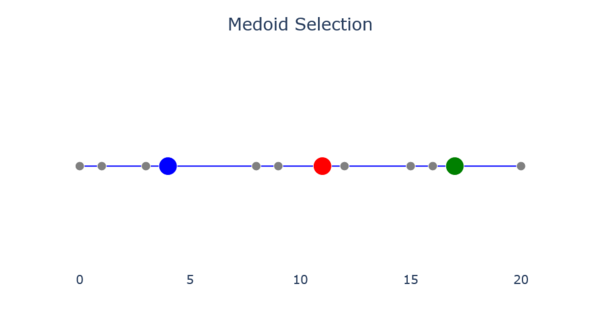
Se repiten los pasos 3 y 4 hasta que los centros ya no se muevan, como en las imágenes siguientes.

• Repitiendo los pasos 3 y 4 (de izquierda a derecha)
• 
  Los segundos cúmulos.
• 
  Selección de medoides.
• 
  Los terceros clusters.
• 
  Selección final de medioide.

Paso 6

Los clústeres finales se obtienen cuando los centros ya no se mueven entre los pasos. La imagen siguiente muestra cómo puede lucir un clúster final.

Los clusters finales.

Paso 7

La variación se suma dentro de cada grupo para ver qué tan precisos son los centros. Al ejecutar esta prueba con diferentes valores K, se puede obtener un " codo " del gráfico de variación, donde la variación del gráfico se nivela. El "codo" del gráfico es el valor K óptimo para el conjunto de datos.

Medoides en altas dimensiones

Un problema común con el agrupamiento de k-medoides y otros algoritmos de agrupamiento basados ​​en medoides es la " maldición de la dimensionalidad ", en la que los puntos de datos contienen demasiadas dimensiones o características. A medida que se agregan dimensiones a los datos, la distancia entre ellos se vuelve escasa ^[24] y se vuelve difícil caracterizar el agrupamiento solo por la distancia euclidiana. Como resultado, las medidas de similitud basadas en la distancia convergen a una constante ^[25] y tenemos una caracterización de la distancia entre puntos que puede no reflejar nuestro conjunto de datos de formas significativas.

Una forma de mitigar los efectos de la maldición de la dimensionalidad es mediante el uso de agrupamiento espectral . El agrupamiento espectral logra un análisis más apropiado al reducir la dimensionalidad de los datos mediante el análisis de componentes principales , proyectando los puntos de datos en el subespacio de menor dimensión y luego ejecutando el algoritmo de agrupamiento elegido como antes. Sin embargo, una cosa a tener en cuenta es que, como con cualquier reducción de dimensión, perdemos información, ^[26] por lo que se debe sopesar con anticipación frente al agrupamiento cuánta reducción es necesaria antes de que se pierdan demasiados datos.

Sin embargo, la alta dimensionalidad no solo afecta las métricas de distancia, ya que la complejidad temporal también aumenta con el número de características. Los k-medoides son sensibles a la elección inicial de los medoides, ya que generalmente se seleccionan aleatoriamente. Dependiendo de cómo se inicialicen dichos medoides, los k-medoides pueden converger a diferentes óptimos locales, lo que da como resultado diferentes grupos y medidas de calidad, ^[27] lo que significa que los k-medoides pueden necesitar ejecutarse varias veces con diferentes inicializaciones, lo que da como resultado un tiempo de ejecución mucho mayor. Una forma de contrarrestar esto es usar k-medoids++, ^[28] una alternativa a los k-medoides similar a su contraparte k-means, k-means++ que elige medoides iniciales para comenzar en función de una distribución de probabilidad, como una especie de "aleatoriedad informada" o una suposición educada, si se quiere. Si se eligen dichos medoides con este razonamiento, el resultado es un tiempo de ejecución mejorado y un mejor rendimiento en la agrupación. El algoritmo k-medoids++ se describe a continuación: ^[29]

1. El medoide inicial se elige aleatoriamente entre todos los puntos espaciales.
2. Para cada punto espacial 𝑝, calcule la distancia entre 𝑝 y los medoides más cercanos, denominada D(𝑝), y sume todas las distancias a 𝑆.
3. El siguiente medoide se determina mediante una distribución de probabilidad ponderada. En concreto, se elige un número aleatorio 𝑅 entre cero y la distancia sumada 𝑆 y el punto espacial correspondiente es el siguiente medoide.
4. Los pasos (2) y (3) se repiten hasta que se hayan elegido 𝑘 medoides.

Ahora que tenemos las primeras selecciones apropiadas para los medoides, se puede ejecutar la variación normal de k-medoides.

Referencias

1. Struyf, Anja; Hubert, Mia ; Rousseeuw, Peter (1997). "Agrupamiento en un entorno orientado a objetos". Revista de software estadístico . 1 (4): 1–30.
2. van der Laan, Mark J. ; Pollard, Katherine S.; Bryan, Jennifer (2003). "Un nuevo algoritmo de partición alrededor de Medoids". Revista de computación estadística y simulación . 73 (8). Grupo Taylor & Francis: 575–584. doi :10.1080/0094965031000136012. S2CID  17437463.
3. Newling, James; y Fleuret, François (2016); "Un algoritmo medoide exacto subcuadrático", en Actas de la 20.ª Conferencia Internacional sobre Inteligencia Artificial y Estadística , PMLR 54:185-193, 2017. Disponible en línea.
4. Bagaria, Vivek; Kamath, Govinda M.; Ntranos, Vasilis; Zhang, Martin J.; Tse, David (2017). "Medoides en tiempo casi lineal mediante bandidos multiarmados". arXiv : 1711.00817 . {{cite journal}}: Requiere citar revista |journal=( ayuda )
5. Hoare, Charles Antony Richard (1961); "Algoritmo 65: encontrar", en Comunicaciones de la ACM , 4 (7), 321-322
6. Eppstein, David ; y Wang, Joseph (2006); "Aproximación rápida de la centralidad", en Graph Algorithms and Applications , 5 , págs. 39-45
7. Okamoto, Kazuya; Chen, Wei; Li, Xiang-Yang (2008). "Ranking de la centralidad de cercanía para redes sociales a gran escala". Frontiers in Algorithmics . Apuntes de clase en informática. Vol. 5059. págs. 186–195. doi :10.1007/978-3-540-69311-6_21. ISBN 978-3-540-69310-9.
8. Baharav, Tavor Z.; y Tse, David N. (2019); "Identificación ultrarrápida de medoides mediante reducción a la mitad secuencial correlacionada", en Advances in Neural Information Processing Systems , disponible en línea
9. Dai, Qiongjie; Liu, Jicheng (julio de 2019). "La exploración y aplicación de K-medoides en la agrupación de textos" (PDF) . Consultado el 25 de abril de 2023 .
10. "¿Qué es el procesamiento del lenguaje natural?"
11. Hu, Po; He, Tingting; Ji, Donghong. "Resumen de textos chinos basado en la detección de áreas temáticas" (PDF) .
12. Pessutto, Lucas; Vargas, Danny; Moreira, Viviane (24 de febrero de 2020). "Agrupamiento de aspectos multilingües para análisis de sentimientos". Knowledge-Based Systems . 192 : 105339. doi :10.1016/j.knosys.2019.105339. S2CID  211830280.
13. Preud'homme, Gregoire; Duarte, Kevin (18 de febrero de 2021). "Comparación directa de métodos de agrupamiento para datos heterogéneos: un punto de referencia basado en simulación". Scientific Reports . 11 (1): 4202. Bibcode :2021NatSR..11.4202P. doi :10.1038/s41598-021-83340-8. PMC 7892576 . PMID  33603019. 
14. Amer, Ali; Abdalla, Hassan (14 de septiembre de 2020). "Una medida de similitud basada en la teoría de conjuntos para la agrupación y clasificación de textos". Journal of Big Data . 7 . doi : 10.1186/s40537-020-00344-3 . S2CID  256403960.
15. Wu, Gang (17 de diciembre de 2022). «Métricas de similitud de cadenas: distancia de edición».
16. Mokhtarani, Shabnam (26 de agosto de 2021). "Integraciones en el aprendizaje automático: todo lo que necesita saber".
17. Wu, Yuexin; Xu, Yichong; Singh, Aarti; Yang, Yiming; Dubrawski, Artur (2019). "Aprendizaje activo para redes neuronales gráficas mediante propagación de características de nodos". arXiv : 1910.07567 [cs.LG].
18. Tiwari, Mo; Mayclin, James; Piech, Chris; Zhang, Martin; Thrun, Sebastian; Shomorony, Ilan (2020). "BanditPAM: ​​Agrupamiento de k-medoides en tiempo casi lineal mediante bandidos multiarmados". arXiv : 2006.06856 [cs.LG].
19. Zhang, Yan; Shi, Weiyu; Sun, Yeqing (17 de febrero de 2023). "Un algoritmo de identificación de módulo genético funcional en datos de expresión génica basado en algoritmo genético y ontología génica". BMC Genomics . 24 (1): 76. doi : 10.1186/s12864-023-09157-z . ISSN  1471-2164. PMC 9936134 . PMID  36797662. 
20. Saha, Sanjit Kumar; Schmitt, Ingo (1 de enero de 2020). "Agrupamiento no TI en el contexto de las redes sociales". Procedia Computer Science . La 11.ª Conferencia internacional sobre sistemas ambientales, redes y tecnologías (ANT) / La 3.ª Conferencia internacional sobre datos emergentes e industria 4.0 (EDI40) / Talleres afiliados. 170 : 1186–1191. doi : 10.1016/j.procs.2020.03.031 . ISSN  1877-0509. S2CID  218812939.
21. Wu, Zengyuan; Jin, Lingmin; Zhao, Jiali; Jing, Lizheng; Chen, Liang (18 de junio de 2022). "Investigación sobre la segmentación de clientes de comercio electrónico a través de un algoritmo de agrupamiento de K-Medoids mejorado". Inteligencia computacional y neurociencia . 2022 : 1–10. doi : 10.1155/2022/9930613 . PMC 9233613 . PMID  35761867. 
22. Midway, Stephen R. (diciembre de 2020). "Principios de visualización de datos eficaz". Patrones . 1 (9): 100141. doi :10.1016/j.patter.2020.100141. PMC 7733875 . PMID  33336199. 
23. https://www.researchgate.net/publication/243777819_Clustering_by_Means_of_Medoids ^{[ URL desnuda ]}
24. "La maldición de la dimensionalidad". 17 de mayo de 2019.
25. "Ventajas y desventajas de K-Means | Aprendizaje automático".
26. "Agrupamiento de K-Means en datos de alta dimensión". 10 de abril de 2022.
27. "¿Cuáles son las principales desventajas de utilizar k-medias para datos de alta dimensión?".^{[ ¿ Fuente autopublicada? ]}
28. Yue, Xia (2015). "Algoritmo de agrupamiento espacial paralelo K-Medoids++ basado en MapReduce". arXiv : 1608.06861 [cs.DC].
29. Yue, Xia (2015). "Algoritmo de agrupamiento espacial paralelo K-Medoids++ basado en MapReduce". arXiv : 1608.06861 [cs.DC].

Enlaces externos

• Video de k-means de StatQuest usado como referencia visual en la sección #Visualización_del_proceso_de_agrupamiento_basado_en_medoides