Teorema de separación de hiperplanos

Sobre la existencia de hiperplanos que separan conjuntos convexos disjuntos

En geometría , el teorema de separación de hiperplanos es un teorema sobre conjuntos convexos disjuntos en un espacio euclidiano n -dimensional . Hay varias versiones bastante similares. En una versión del teorema, si ambos conjuntos son cerrados y al menos uno de ellos es compacto , entonces hay un hiperplano entre ellos e incluso dos hiperplanos paralelos entre ellos separados por un espacio. En otra versión, si ambos conjuntos convexos disjuntos son abiertos, entonces hay un hiperplano entre ellos, pero no necesariamente ningún espacio. Un eje que es ortogonal a un hiperplano separador es un eje separador , porque las proyecciones ortogonales de los cuerpos convexos sobre el eje son disjuntas.

El teorema de separación de hiperplanos se debe a Hermann Minkowski . El teorema de separación de Hahn-Banach generaliza el resultado a espacios vectoriales topológicos .

Un resultado relacionado es el teorema del hiperplano de apoyo .

En el contexto de las máquinas de vectores de soporte , el hiperplano de separación óptima o hiperplano de margen máximo es un hiperplano que separa dos capas convexas de puntos y es equidistante de los dos. ^{[1] [2] [3]}

Afirmaciones y pruebas

Teorema de separación de hiperplanos ^[4]  —  Sean y dos subconjuntos convexos no vacíos y disjuntos de . Entonces existe un vector distinto de cero y un número real tales que ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle v}$ ${\displaystyle c}$

${\displaystyle \langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c}$

para todo en y en ; es decir, el hiperplano , el vector normal, separa y . ${\displaystyle x}$ ${\displaystyle A}$ ${\displaystyle y}$ ${\displaystyle B}$ ${\displaystyle \langle \cdot ,v\rangle =c}$ ${\displaystyle v}$ ${\displaystyle A}$ ${\displaystyle B}$

Si ambos conjuntos son cerrados, y al menos uno de ellos es compacto, entonces la separación puede ser estricta, es decir, para algún ${\displaystyle \langle x,v\rangle >c_{1}\,{\text{ and }}\langle y,v\rangle <c_{2}}$ ${\displaystyle c_{1}>c_{2}}$

En todos los casos, se supone que son subconjuntos disjuntos, no vacíos y convexos de . El resumen de los resultados es el siguiente: ${\displaystyle A,B}$ ${\displaystyle \mathbb {R} ^{n}}$

El número de dimensiones debe ser finito. En espacios de dimensión infinita hay ejemplos de dos conjuntos cerrados, convexos y disjuntos que no pueden separarse mediante un hiperplano cerrado (un hiperplano donde una función lineal continua es igual a alguna constante) incluso en el sentido débil donde las desigualdades no son estrictas. ^[5]

En este caso, no se puede relajar la compacidad de la hipótesis; véase un ejemplo en la sección Contraejemplos y unicidad. Esta versión del teorema de separación se generaliza a dimensiones infinitas; la generalización se conoce más comúnmente como el teorema de separación de Hahn-Banach .

La prueba se basa en el siguiente lema:

Lema  —  Sean y dos subconjuntos cerrados disjuntos de , y supongamos que es compacto. Entonces existen puntos y que minimizan la distancia sobre y . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle A}$ ${\displaystyle a_{0}\in A}$ ${\displaystyle b_{0}\in B}$ ${\displaystyle \|a-b\|}$ ${\displaystyle a\in A}$ ${\displaystyle b\in B}$

Prueba del lema

Sea y cualquier par de puntos, y sea . Como es compacto, está contenido en alguna bola centrada en ; sea el radio de esta bola . Sea la intersección de con una bola cerrada de radio alrededor de . Entonces es compacto y no vacío porque contiene a . Como la función de distancia es continua, existen puntos y cuya distancia es la mínima sobre todos los pares de puntos en . Queda por demostrar que y de hecho tienen la distancia mínima sobre todos los pares de puntos en . Supóngase por contradicción que existen puntos y tales que . Entonces en particular, , y por la desigualdad triangular, . Por lo tanto está contenido en , lo que contradice el hecho de que y tenían una distancia mínima sobre . ${\displaystyle a\in A}$ ${\displaystyle b\in B}$ ${\displaystyle r_{1}=\|b-a\|}$ ${\displaystyle A}$ ${\displaystyle a}$ ${\displaystyle r_{2}}$ ${\displaystyle S=B\cap {\overline {B_{r_{1}+r_{2}}(a)}}}$ ${\displaystyle B}$ ${\displaystyle r_{1}+r_{2}}$ ${\displaystyle a}$ ${\displaystyle S}$ ${\displaystyle b}$ ${\displaystyle a_{0}}$ ${\displaystyle b_{0}}$ ${\displaystyle \|a_{0}-b_{0}\|}$ ${\displaystyle A\times S}$ ${\displaystyle a_{0}}$ ${\displaystyle b_{0}}$ ${\displaystyle A\times B}$ ${\displaystyle a'}$ ${\displaystyle b'}$ ${\displaystyle \|a'-b'\|<\|a_{0}-b_{0}\|}$ ${\displaystyle \|a'-b'\|<r_{1}}$ ${\displaystyle \|a-b'\|\leq \|a'-b'\|+\|a-a'\|<r_{1}+r_{2}}$ ${\displaystyle b'}$ ${\displaystyle S}$ ${\displaystyle a_{0}}$ ${\displaystyle b_{0}}$ ${\displaystyle A\times S}$ ${\displaystyle \square }$

Ilustración de prueba.

Prueba del teorema

Primero demostramos el segundo caso. (Véase el diagrama.)

WLOG, es compacto. Por el lema, existen puntos y de distancia mínima entre sí. Como y son disjuntos, tenemos . Ahora, construya dos hiperplanos perpendiculares al segmento de línea , con lados y lados . Afirmamos que ni ni entra en el espacio entre , y por lo tanto los hiperplanos perpendiculares satisfacen el requisito del teorema. ${\displaystyle A}$ ${\displaystyle a_{0}\in A}$ ${\displaystyle b_{0}\in B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle a_{0}\neq b_{0}}$ ${\displaystyle L_{A},L_{B}}$ ${\displaystyle [a_{0},b_{0}]}$ ${\displaystyle L_{A}}$ ${\displaystyle a_{0}}$ ${\displaystyle L_{B}}$ ${\displaystyle b_{0}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle L_{A},L_{B}}$ ${\displaystyle (a_{0},b_{0})}$

Algebraicamente, los hiperplanos están definidos por el vector , y dos constantes , tales que . Nuestra afirmación es que y . ${\displaystyle L_{A},L_{B}}$ ${\displaystyle v:=b_{0}-a_{0}}$ ${\displaystyle c_{A}:=\langle v,a_{0}\rangle <c_{B}:=\langle v,b_{0}\rangle }$ ${\displaystyle L_{A}=\{x:\langle v,x\rangle =c_{A}\},L_{B}=\{x:\langle v,x\rangle =c_{B}\}}$ ${\displaystyle \forall a\in A,\langle v,a\rangle \leq c_{A}}$ ${\displaystyle \forall b\in B,\langle v,b\rangle \geq c_{B}}$

Supóngase que existe algún tal que , entonces sea el pie de la perpendicular desde al segmento de línea . Como es convexo, está dentro de , y por geometría plana, está más cerca de que , contradicción. Un argumento similar se aplica a . ${\displaystyle a\in A}$ ${\displaystyle \langle v,a\rangle >c_{A}}$ ${\displaystyle a'}$ ${\displaystyle b_{0}}$ ${\displaystyle [a_{0},a]}$ ${\displaystyle A}$ ${\displaystyle a'}$ ${\displaystyle A}$ ${\displaystyle a'}$ ${\displaystyle b_{0}}$ ${\displaystyle a_{0}}$ ${\displaystyle B}$

Ahora, el primer caso.

Abordar ambos desde el interior mediante y , de modo que cada uno sea cerrado y compacto, y las uniones sean los interiores relativos . (Ver la página de interiores relativos para más detalles). ${\displaystyle A,B}$ ${\displaystyle A_{1}\subseteq A_{2}\subseteq \cdots \subseteq A}$ ${\displaystyle B_{1}\subseteq B_{2}\subseteq \cdots \subseteq B}$ ${\displaystyle A_{k},B_{k}}$ ${\displaystyle \mathrm {relint} (A),\mathrm {relint} (B)}$

Ahora, en el segundo caso, para cada par existe algún vector unitario y número real , tal que . ${\displaystyle A_{k},B_{k}}$ ${\displaystyle v_{k}}$ ${\displaystyle c_{k}}$ ${\displaystyle \langle v_{k},A_{k}\rangle <c_{k}<\langle v_{k},B_{k}\rangle }$

Como la esfera unitaria es compacta, podemos tomar una subsucesión convergente, de modo que . Sea . Afirmamos que , separando así . ${\displaystyle v_{k}\to v}$ ${\displaystyle c_{A}:=\sup _{a\in A}\langle v,a\rangle ,c_{B}:=\inf _{b\in B}\langle v,b\rangle }$ ${\displaystyle c_{A}\leq c_{B}}$ ${\displaystyle A,B}$

Supongamos que no, entonces existe algún tal que , entonces como , para suficientemente grande , tenemos , contradicción. ${\displaystyle a\in A,b\in B}$ ${\displaystyle \langle v,a\rangle >\langle v,b\rangle }$ ${\displaystyle v_{k}\to v}$ ${\displaystyle k}$ ${\displaystyle \langle v_{k},a\rangle >\langle v_{k},b\rangle }$

Como un hiperplano separador no puede intersecar los interiores de conjuntos convexos abiertos, tenemos un corolario:

Teorema de separación I  —  Sean y dos conjuntos convexos no vacíos y disjuntos. Si es abierto, entonces existe un vector distinto de cero y un número real tal que ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle v}$ ${\displaystyle c}$

${\displaystyle \langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle \leq c}$

para todos en y en . Si ambos conjuntos son abiertos, entonces existe un vector distinto de cero y un número real tal que ${\displaystyle x}$ ${\displaystyle A}$ ${\displaystyle y}$ ${\displaystyle B}$ ${\displaystyle v}$ ${\displaystyle c}$

${\displaystyle \langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle <c}$

para todos en y en . ${\displaystyle x}$ ${\displaystyle A}$ ${\displaystyle y}$ ${\displaystyle B}$

Caso con posibles intersecciones

Si los conjuntos tienen posibles intersecciones, pero sus interiores relativos son disjuntos, entonces la prueba del primer caso todavía se aplica sin cambios, obteniéndose así: ${\displaystyle A,B}$

Teorema de separación II  —  Sean y dos subconjuntos convexos no vacíos de con interiores relativos disjuntos. Entonces existe un vector distinto de cero y un número real tales que ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle v}$ ${\displaystyle c}$

${\displaystyle \langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c}$

En particular, tenemos el teorema del hiperplano de apoyo .

Teorema del hiperplano de apoyo  :  si es un conjunto convexo en y es un punto en el límite de , entonces existe un hiperplano de apoyo de que contiene a . ${\displaystyle A}$ ${\displaystyle \mathbb {R} ^{n},}$ ${\displaystyle a_{0}}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle a_{0}}$

Prueba

Si el lapso afín de no es todo , entonces extienda el lapso afín a un hiperplano de soporte. De lo contrario, es disjunto de , por lo que se aplica el teorema anterior. ${\displaystyle A}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathrm {relint} (A)=\mathrm {int} (A)}$ ${\displaystyle \mathrm {relint} (\{a_{0}\})=\{a_{0}\}}$

Inverso del teorema

Obsérvese que la existencia de un hiperplano que sólo "separa" dos conjuntos convexos en el sentido débil de que ambas desigualdades no son estrictas obviamente no implica que los dos conjuntos sean disjuntos. Ambos conjuntos podrían tener puntos ubicados en el hiperplano.

Contraejemplos y unicidad

El teorema no se aplica si uno de los cuerpos no es convexo.

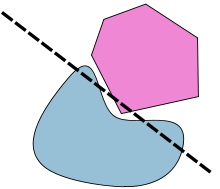
Si uno de los dos , A o B, no es convexo, entonces hay muchos contraejemplos posibles. Por ejemplo, A y B podrían ser círculos concéntricos. Un contraejemplo más sutil es aquel en el que A y B son ambos cerrados pero ninguno es compacto. Por ejemplo, si A es un semiplano cerrado y B está limitado por un brazo de una hipérbola, entonces no hay ningún hiperplano estrictamente separador:

${\displaystyle A=\{(x,y):x\leq 0\}}$

${\displaystyle B=\{(x,y):x>0,y\geq 1/x\}.\ }$

(Aunque, por una instancia del segundo teorema, hay un hiperplano que separa sus interiores.) Otro tipo de contraejemplo tiene A compacto y B abierto. Por ejemplo, A puede ser un cuadrado cerrado y B puede ser un cuadrado abierto que toca a A.

En la primera versión del teorema, evidentemente el hiperplano separador nunca es único. En la segunda versión, puede ser único o no. Técnicamente, un eje separador nunca es único porque puede trasladarse; en la segunda versión del teorema, un eje separador puede ser único hasta la traslación.

El ángulo de cuerno proporciona un buen contraejemplo para muchas separaciones de hiperplanos. Por ejemplo, en , el disco unitario es disjunto del intervalo abierto , pero la única línea que los separa contiene la totalidad de . Esto muestra que si es cerrado y es relativamente abierto, entonces no existe necesariamente una separación que sea estricta para . Sin embargo, si es un politopo cerrado , entonces existe dicha separación. ^[6] ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle ((1,0),(1,1))}$ ${\displaystyle ((1,0),(1,1))}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$

Más variantes

El lema de Farkas y los resultados relacionados pueden entenderse como teoremas de separación de hiperplanos cuando los cuerpos convexos están definidos por un número finito de desigualdades lineales.

Se pueden encontrar más resultados. ^[6]

Uso en detección de colisiones

En la detección de colisiones, el teorema de separación de hiperplanos se utiliza normalmente de la siguiente forma:

Teorema del eje de separación  :  dos objetos convexos cerrados son disjuntos si existe una línea ("eje de separación") sobre la cual las proyecciones de los dos objetos son disjuntas.

Independientemente de la dimensionalidad, el eje de separación siempre es una línea. Por ejemplo, en 3D, el espacio está separado por planos, pero el eje de separación es perpendicular al plano de separación.

El teorema del eje de separación se puede aplicar para la detección rápida de colisiones entre mallas poligonales. La dirección normal u otra característica de cada cara se utiliza como eje de separación. Tenga en cuenta que esto produce posibles ejes de separación, no líneas o planos de separación.

En 3D, el uso exclusivo de las normales de las caras no logrará separar algunos casos de bordes que no colisionan. Se requieren ejes adicionales, que consisten en los productos cruzados de pares de bordes, uno tomado de cada objeto. ^[7]

Para aumentar la eficiencia, los ejes paralelos pueden calcularse como un solo eje.

Véase también

• Cono doble
• El lema de Farkas
• Teorema de Kirchberger
• Control óptimo

Notas

1. Hastie, Trevor ; Tibshirani, Robert ; Friedman, Jerome (2008). Los elementos del aprendizaje estadístico: minería de datos, inferencia y predicción (PDF) (segunda edición). Nueva York: Springer. págs. 129–135.
2. Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. (2016). Minería de datos: herramientas y técnicas prácticas de aprendizaje automático (cuarta edición). Morgan Kaufmann. págs. 253–254. ISBN 9780128043578.
3. Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Matemáticas para el aprendizaje automático . Cambridge University Press. págs. 337–338. ISBN 978-1-108-45514-5.
4. Boyd y Vandenberghe 2004, ejercicio 2.22.
5. Haïm Brezis , Analizar funciones: teoría y aplicaciones , 1983, comentario 4, p. 7.
6. Stoer, Josef; Witzgall, Christoph (1970). Convexidad y optimización en dimensiones finitas I. Springer Berlin, Heidelberg. (2.12.9). doi :10.1007/978-3-642-46216-0. ISBN 978-3-642-46216-0.
7. "Matemáticas vectoriales avanzadas".

Referencias

• Boyd, Stephen P.; Vandenberghe, Lieven (2004). Optimización convexa (PDF) . Cambridge University Press. ISBN 978-0-521-83378-3.
• Golshtein, EG; Tretyakov, NV (1996). Lagrangianos modificados y mapas monótonos en optimización . Nueva York: Wiley. p. 6. ISBN 0-471-54821-9.
• Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Programación matemática no diferenciable y de dos niveles . Boston: Kluwer Academic Publishers. pág. 19. ISBN 0-7923-9821-1.

• Soltan, V. (2021). Propiedades de soporte y separación de conjuntos convexos en dimensión finita . Extracta Math. Vol. 36, núm. 2, 241-278.

Enlaces externos

• Detección y respuesta ante colisiones