Masa efectiva (física del estado sólido)

Masa de una partícula al interactuar con otras partículas

En física del estado sólido , la masa efectiva de una partícula (a menudo denominada ) es la masa que parece tener cuando responde a fuerzas, o la masa que parece tener cuando interactúa con otras partículas idénticas en una distribución térmica . Uno de los resultados de la teoría de bandas de los sólidos es que el movimiento de partículas en un potencial periódico, a lo largo de largas distancias mayores que el espaciamiento reticular, puede ser muy diferente de su movimiento en el vacío. La masa efectiva es una cantidad que se utiliza para simplificar las estructuras de bandas al modelar el comportamiento de una partícula libre con esa masa. Para algunos propósitos y algunos materiales, la masa efectiva puede considerarse una constante simple de un material. En general, sin embargo, el valor de la masa efectiva depende del propósito para el que se utiliza y puede variar según una serie de factores. ${\textstyle m^{*}}$

En el caso de los electrones o los huecos de electrones en un sólido, la masa efectiva suele expresarse como un factor que multiplica la masa en reposo de un electrón , m _e (9,11 × 10 ⁻³¹ kg). Este factor suele estar en el rango de 0,01 a 10, pero puede ser menor o mayor (por ejemplo, alcanzando 1000 en materiales exóticos de fermiones pesados ), o en cualquier valor entre cero e infinito (según la definición) en el grafeno . Dado que simplifica la teoría de bandas más general, la masa electrónica efectiva puede considerarse un parámetro básico importante que influye en las propiedades mensurables de un sólido, que incluyen todo, desde la eficiencia de una célula solar hasta la velocidad de un circuito integrado.

Caso simple: relación de dispersión parabólica e isótropa

En las energías más altas de la banda de valencia en muchos semiconductores (Ge, Si, GaAs, ...), y las energías más bajas de la banda de conducción en algunos semiconductores (GaAs, ...), la estructura de banda E ( k ) se puede aproximar localmente como

${\displaystyle E(\mathbf {k} )=E_{0}+{\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m^{*}}}}$

donde E ( k ) es la energía de un electrón en el vector de onda k en esa banda, E ₀ es una constante que da el borde de energía de esa banda, y m ^* es una constante (la masa efectiva).

Se puede demostrar que los electrones ubicados en estas bandas se comportan como electrones libres, excepto que tienen una masa diferente, siempre que su energía se mantenga dentro del rango de validez de la aproximación anterior. Como resultado, la masa del electrón en modelos como el modelo de Drude debe reemplazarse por la masa efectiva.

Una propiedad notable es que la masa efectiva puede volverse negativa cuando la banda se curva hacia abajo alejándose de un máximo. Como resultado de la masa negativa , los electrones responden a las fuerzas eléctricas y magnéticas ganando velocidad en la dirección opuesta a la normal; aunque estos electrones tienen carga negativa, se mueven en trayectorias como si tuvieran carga positiva (y masa positiva). Esto explica la existencia de huecos en la banda de valencia , las cuasipartículas de carga positiva y masa positiva que se pueden encontrar en los semiconductores. ^[1]

En cualquier caso, si la estructura de bandas tiene la forma parabólica simple descrita anteriormente, entonces el valor de la masa efectiva es inequívoco. Desafortunadamente, esta forma parabólica no es válida para describir la mayoría de los materiales. En materiales tan complejos no existe una única definición de "masa efectiva", sino múltiples definiciones, cada una de ellas adecuada a un propósito particular. El resto del artículo describe estas masas efectivas en detalle.

Caso intermedio: relación de dispersión parabólica y anisotrópica

Elipsoides de energía constante en silicio cerca de los mínimos de seis bandas de conducción. Para cada valle (mínimo de banda), las masas efectivas son m _ℓ = 0,92 m _e ("longitudinal"; a lo largo de un eje) y m _t = 0,19 m _e ("transversal"; a lo largo de dos ejes). ^[2]

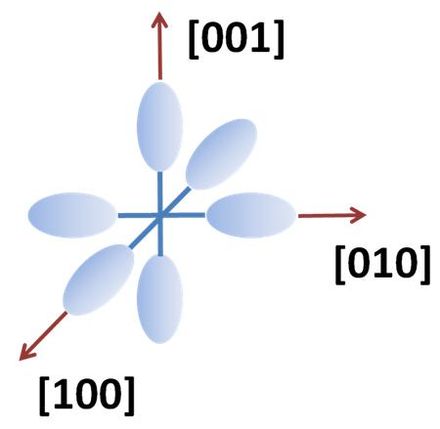
En algunos semiconductores importantes (en particular, el silicio), las energías más bajas de la banda de conducción no son simétricas, ya que las superficies de energía constante son ahora elipsoides , en lugar de esferas en el caso isotrópico. Cada mínimo de la banda de conducción se puede aproximar solo mediante

${\displaystyle E\left(\mathbf {k} \right)=E_{0}+{\frac {\hbar ^{2}}{2m_{x}^{*}}}\left(k_{x}-k_{0,x}\right)^{2}+{\frac {\hbar ^{2}}{2m_{y}^{*}}}\left(k_{y}-k_{0,y}\right)^{2}+{\frac {\hbar ^{2}}{2m_{z}^{*}}}\left(k_{z}-k_{0,z}\right)^{2}}$

donde los ejes x , y y z están alineados con los ejes principales de los elipsoides, y m^*
_x, yo^*
_yy yo^*
_yson las masas efectivas inerciales a lo largo de estos diferentes ejes. Los desplazamientos k _{0, x} , k _{0, y} y k _{0, z} reflejan que el mínimo de la banda de conducción ya no está centrado en el vector de onda cero. (Estas masas efectivas corresponden a los componentes principales del tensor de masa efectiva inercial, descrito más adelante. ^[3] )

En este caso, el movimiento del electrón ya no es directamente comparable al de un electrón libre; la velocidad de un electrón dependerá de su dirección y se acelerará en un grado diferente según la dirección de la fuerza. Aun así, en cristales como el silicio, las propiedades generales, como la conductividad, parecen ser isotrópicas. Esto se debe a que hay múltiples valles (mínimos de la banda de conducción), cada uno con masas efectivas reorganizadas a lo largo de diferentes ejes. Los valles actúan colectivamente juntos para dar una conductividad isotrópica. Es posible promediar las masas efectivas de los diferentes ejes de alguna manera, para recuperar la imagen del electrón libre. Sin embargo, el método de promediado resulta depender del propósito: ^[4]

• Para el cálculo de la densidad total de estados y la densidad total de portadores, mediante la media geométrica combinada con un factor de degeneración g que cuenta el número de valles (en silicio g = 6 ): ^[3]

  ${\displaystyle m_{\text{density}}^{*}={\sqrt[{3}]{g^{2}m_{x}m_{y}m_{z}}}}$

  (Esta masa efectiva corresponde a la masa efectiva de la densidad de estados, descrita más adelante.)

  Para la densidad de estados por valle y la densidad de portadores por valle, se omite el factor de degeneración.
• Para efectos de calcular la conductividad como en el modelo de Drude, a través de la media armónica

  ${\displaystyle m_{\text{conductivity}}^{*}=3\left[{\frac {1}{m_{x}^{*}}}+{\frac {1}{m_{y}^{*}}}+{\frac {1}{m_{z}^{*}}}\right]^{-1}}$

  Dado que la ley de Drude también depende del tiempo de dispersión, que varía mucho, esta masa efectiva rara vez se utiliza; en cambio, la conductividad suele expresarse en términos de densidad de portadores y un parámetro medido empíricamente, la movilidad de los portadores .

Caso general

En general, la relación de dispersión no se puede aproximar como parabólica y, en tales casos, la masa efectiva debe definirse con precisión si se va a utilizar. Aquí, una definición comúnmente establecida de masa efectiva es el tensor de masa efectiva inercial definido a continuación; sin embargo, en general es una función matricial del vector de onda, e incluso más compleja que la estructura de bandas. Otras masas efectivas son más relevantes para los fenómenos directamente medibles.

Tensor de masa inercial efectivo

Una partícula clásica bajo la influencia de una fuerza se acelera de acuerdo con la segunda ley de Newton , a = m ⁻¹ F , o alternativamente, el momento cambia de acuerdo con ⁠d/el o⁠ p = F . Este principio intuitivo aparece de forma idéntica en aproximaciones semiclásicas derivadas de la estructura de bandas cuando las transiciones entre bandas pueden ignorarse para campos externos suficientemente débiles. ^{[5] [6]} La fuerza da una tasa de cambio en el momento del cristal p _cristal :

${\displaystyle \mathbf {F} ={\frac {\operatorname {d} \mathbf {p} _{\text{crystal}}}{\operatorname {d} t}}=\hbar {\frac {\operatorname {d} \mathbf {k} }{\operatorname {d} t}},}$

donde ħ = h /2π es la constante de Planck reducida .

La aceleración de una partícula ondulatoria se convierte en la tasa de cambio en la velocidad del grupo :

${\displaystyle \mathbf {a} ={\frac {\operatorname {d} }{\operatorname {d} t}}\,\mathbf {v} _{\text{g}}={\frac {\operatorname {d} }{\operatorname {d} t}}\left(\nabla _{k}\,\omega \left(\mathbf {k} \right)\right)=\nabla _{k}{\frac {\operatorname {d} \omega \left(\mathbf {k} \right)}{\operatorname {d} t}}=\nabla _{k}\left({\frac {\operatorname {d} \mathbf {k} }{\operatorname {d} t}}\cdot \nabla _{k}\,\omega (\mathbf {k} )\right),}$

donde ∇ _k es el operador del en el espacio recíproco . El último paso se deriva del uso de la regla de la cadena para una derivada total para una cantidad con dependencias indirectas , porque el resultado directo de la fuerza es el cambio en k ( t ) dado anteriormente, que indirectamente resulta en un cambio en E ( k )= ħ ω( k ) . Combinando estas dos ecuaciones se obtiene

${\displaystyle \mathbf {a} =\nabla _{k}\left({\frac {\mathbf {F} }{\hbar }}\cdot \nabla _{k}\,{\frac {E(\mathbf {k} )}{\hbar }}\right)={\frac {1}{\hbar ^{2}}}\left(\nabla _{k}\left(\nabla _{k}\,E(\mathbf {k} )\right)\right)\cdot \mathbf {F} =M_{\text{inert}}^{-1}\cdot \mathbf {F} }$

Utilizando la regla del producto escalar con una fuerza uniforme ( ∇ _k F =0 ). es la matriz hessiana de E ( k ) en el espacio recíproco. Vemos que el equivalente de la masa inercial recíproca newtoniana para una partícula libre definida por a = m ⁻¹ F se ha convertido en una cantidad tensorial ${\displaystyle \nabla _{k}\left(\nabla _{k}\,E(\mathbf {k} )\right)}$

${\displaystyle M_{\text{inert}}^{-1}={\frac {1}{\hbar ^{2}}}\nabla _{k}\left(\nabla _{k}\,E(\mathbf {k} )\right).}$

cuyos elementos son

${\displaystyle \left[M_{\text{inert}}^{-1}\right]_{ij}={\frac {1}{\hbar ^{2}}}\left[\nabla _{k}\left(\nabla _{k}\,E(\mathbf {k} )\right)\right]_{ij}={\frac {1}{\hbar ^{2}}}{\frac {\partial ^{2}E}{\partial k_{i}\partial k_{j}}}\,.}$

Este tensor permite que la aceleración y la fuerza estén en direcciones diferentes, y que la magnitud de la aceleración dependa de la dirección de la fuerza.

• Para las bandas parabólicas, los elementos fuera de la diagonal de Minert ⁻¹ son cero y los elementos diagonales son constantes _.
• Para las bandas isótropas, los elementos diagonales deben ser todos iguales y los elementos fuera de la diagonal deben ser todos iguales.
• Para bandas isotrópicas parabólicas, M _inerte ⁻¹ = ⁠1/yo ^*⁠ I , donde m ^* es una masa efectiva escalar e I es la identidad.
• En general, los elementos de M _inert ⁻¹ son funciones de k .
• La inversa, M _inert = ( M _inert ⁻¹ ) ⁻¹ , se conoce como tensor de masa efectiva . Nótese que no siempre es posible invertir M _inert ⁻¹

Para bandas con dispersión lineal como con fotones o electrones en grafeno , la velocidad de grupo es fija, es decir, los electrones que viajan en paralelo con k a la dirección de fuerza F no pueden ser acelerados y los elementos diagonales de M _inert ⁻¹ son obviamente cero. Sin embargo, los electrones que viajan con un componente perpendicular a la fuerza pueden ser acelerados en la dirección de la fuerza, y los elementos fuera de la diagonal de M _inert ⁻¹ no son cero. De hecho, los elementos fuera de la diagonal escalan inversamente con k , es decir, divergen (se vuelven infinitos) para k pequeño . Es por eso que a veces se dice que los electrones en grafeno tienen masa infinita (debido a los ceros en la diagonal de M _inert ⁻¹ ) y a veces se dice que no tienen masa (debido a la divergencia en las diagonales fuera de la diagonal). ^[7] ${\displaystyle E\propto k}$

Masa efectiva del ciclotrón

Clásicamente, una partícula cargada en un campo magnético se mueve en una hélice a lo largo del eje del campo magnético. El período T de su movimiento depende de su masa m y su carga e .

${\displaystyle T=\left\vert {\frac {2\pi m}{eB}}\right\vert }$

donde B es la densidad de flujo magnético .

En el caso de las partículas con estructuras de bandas asimétricas, ya no se mueven exactamente en una hélice, sino que su movimiento transversal al campo magnético sigue moviéndose en un bucle cerrado (no necesariamente un círculo). Además, el tiempo necesario para completar uno de estos bucles sigue variando inversamente al campo magnético, por lo que es posible definir una masa efectiva del ciclotrón a partir del período medido, utilizando la ecuación anterior.

El movimiento semiclásico de la partícula se puede describir mediante un bucle cerrado en el espacio k. A lo largo de este bucle, la partícula mantiene una energía constante, así como un momento constante a lo largo del eje del campo magnético. Al definir A como el área del espacio k encerrada por este bucle (esta área depende de la energía E , la dirección del campo magnético y el vector de onda en el eje k _B ), se puede demostrar que la masa efectiva del ciclotrón depende de la estructura de bandas a través de la derivada de esta área en energía:

${\displaystyle m^{*}\left(E,{\hat {B}},k_{\hat {B}}\right)={\frac {\hbar ^{2}}{2\pi }}\cdot {\frac {\partial }{\partial E}}A\left(E,{\hat {B}},k_{\hat {B}}\right)}$

Normalmente, los experimentos que miden el movimiento del ciclotrón ( resonancia ciclotrón , efecto De Haas-Van Alphen , etc.) se limitan a sondear únicamente el movimiento para energías cercanas al nivel de Fermi .

En los gases electrónicos bidimensionales , la masa efectiva del ciclotrón se define solo para una dirección del campo magnético (perpendicular) y el vector de onda fuera del plano se elimina. Por lo tanto, la masa efectiva del ciclotrón es solo una función de la energía y resulta estar exactamente relacionada con la densidad de estados en esa energía a través de la relación , donde g _v es la degeneración del valle. Una relación tan simple no se aplica en materiales tridimensionales. ${\displaystyle \scriptstyle g(E)\;=\;{\frac {g_{v}m^{*}}{\pi \hbar ^{2}}}}$

Densidad de estados de masas efectivas (semiconductores ligeramente dopados)

En semiconductores con bajos niveles de dopaje, la concentración de electrones en la banda de conducción viene dada en general por

${\displaystyle n_{\text{e}}=N_{\text{C}}\exp \left(-{\frac {E_{\text{C}}-E_{\text{F}}}{kT}}\right)}$

donde E _F es el nivel de Fermi , E _C es la energía mínima de la banda de conducción y N _C es un coeficiente de concentración que depende de la temperatura. Se puede demostrar que la relación anterior para n _e se aplica a cualquier forma de banda de conducción (incluidas las bandas asimétricas no parabólicas), siempre que el dopaje sea débil ( E _C − E _F ≫ kT ); esto es una consecuencia de las estadísticas de Fermi-Dirac que limitan hacia las estadísticas de Maxwell-Boltzmann .

El concepto de masa efectiva es útil para modelar la dependencia de la temperatura de N _C , lo que permite utilizar la relación anterior en un rango de temperaturas. En un material tridimensional idealizado con una banda parabólica, el coeficiente de concentración viene dado por

${\displaystyle \quad N_{\text{C}}=2\left({\frac {2\pi m_{\text{e}}^{*}kT}{h^{2}}}\right)^{\frac {3}{2}}}$

En semiconductores con estructuras de bandas no simples, esta relación se utiliza para definir una masa efectiva, conocida como densidad de estados masa efectiva de electrones . El nombre "masa efectiva de densidad de estados" se utiliza porque la expresión anterior para N _C se deriva a través de la densidad de estados para una banda parabólica.

En la práctica, la masa efectiva extraída de esta manera no es del todo constante en temperatura ( N _C no varía exactamente como T ^3/2 ). En el silicio, por ejemplo, esta masa efectiva varía en un pequeño porcentaje entre el cero absoluto y la temperatura ambiente porque la estructura de bandas en sí misma cambia ligeramente de forma. Estas distorsiones de la estructura de bandas son el resultado de cambios en las energías de interacción electrón-fonón, en las que la expansión térmica de la red juega un papel menor. ^[8]

De manera similar, el número de huecos en la banda de valencia y la densidad de estados de masa efectiva de huecos se definen mediante:

${\displaystyle n_{\text{h}}=N_{\text{V}}\exp \left(-{\frac {E_{\text{F}}-E_{\text{V}}}{kT}}\right),\quad N_{\text{V}}=2\left({\frac {2\pi m_{\text{h}}^{*}kT}{h^{2}}}\right)^{\frac {3}{2}}}$

donde EV es la energía máxima de la banda de valencia. En la práctica, esta masa efectiva tiende a variar mucho entre el cero absoluto y la temperatura ambiente en muchos materiales ₍ por ejemplo, un factor de dos en el silicio), ya que hay múltiples bandas de valencia con un carácter distinto y significativamente no parabólico, todas con un pico cerca de la misma energía. ^[8]

Determinación

Experimental

Tradicionalmente, las masas efectivas se medían utilizando resonancia ciclotrónica , un método en el que la absorción de microondas de un semiconductor inmerso en un campo magnético pasa por un pico agudo cuando la frecuencia de microondas es igual a la frecuencia del ciclotrón . En los últimos años, las masas efectivas se han determinado más comúnmente a través de la medición de estructuras de banda utilizando técnicas como la espectroscopia de fotoemisión con resolución angular ( ARPES ) o, más directamente, el efecto de Haas-van Alphen . Las masas efectivas también se pueden estimar utilizando el coeficiente γ del término lineal en el calor específico electrónico de baja temperatura a volumen constante . El calor específico depende de la masa efectiva a través de la densidad de estados en el nivel de Fermi y, como tal, es una medida de degeneración y curvatura de banda. Estimaciones muy grandes de la masa del portador a partir de mediciones de calor específico han dado lugar al concepto de materiales fermiónicos pesados . Dado que la movilidad del portador depende de la relación entre la vida útil de la colisión del portador y la masa efectiva, las masas se pueden determinar en principio a partir de mediciones de transporte, pero este método no es práctico ya que las probabilidades de colisión del portador normalmente no se conocen a priori. El efecto Hall óptico es una técnica emergente para medir la densidad de portadores de carga libres, la masa efectiva y los parámetros de movilidad en semiconductores. El efecto Hall óptico mide el análogo del efecto Hall eléctrico inducido por un campo eléctrico cuasiestático a frecuencias ópticas en materiales conductivos y estratificados complejos. El efecto Hall óptico también permite caracterizar la anisotropía (carácter tensorial) de la masa efectiva y los parámetros de movilidad. ^{[12] [13]} ${\displaystyle \scriptstyle f_{c}\;=\;{\frac {eB}{2\pi m^{*}}}}$ ${\displaystyle \scriptstyle c_{v}}$ ${\displaystyle \tau }$

Teorético

Se utilizan diversos métodos teóricos, entre ellos la teoría del funcional de la densidad , la teoría de perturbación k·p y otros , para complementar y respaldar las diversas mediciones experimentales descritas en la sección anterior, incluida la interpretación, el ajuste y la extrapolación de estas mediciones. Algunos de estos métodos teóricos también se pueden utilizar para realizar predicciones ab initio de la masa efectiva en ausencia de datos experimentales, por ejemplo, para estudiar materiales que aún no se han creado en el laboratorio.

Significado

La masa efectiva se utiliza en cálculos de transporte, como el transporte de electrones bajo la influencia de campos o gradientes de portadores, pero también se utiliza para calcular la densidad de portadores y la densidad de estados en semiconductores. Estas masas están relacionadas pero, como se explicó en las secciones anteriores, no son las mismas porque las ponderaciones de varias direcciones y vectores de onda son diferentes. Estas diferencias son importantes, por ejemplo en materiales termoeléctricos , donde se desea una alta conductividad, generalmente asociada con masa ligera, al mismo tiempo que un alto coeficiente de Seebeck , generalmente asociado con masa pesada. Se han desarrollado métodos para evaluar las estructuras electrónicas de diferentes materiales en este contexto. ^[14]

Ciertos compuestos del grupo III - V , como el arseniuro de galio (GaAs) y el antimoniuro de indio (InSb), tienen masas efectivas mucho menores que los materiales tetraédricos del grupo IV, como el silicio y el germanio . En la imagen más simple de transporte electrónico de Drude, la velocidad máxima del portador de carga obtenible es inversamente proporcional a la masa efectiva: , donde con es la carga electrónica . La velocidad máxima de los circuitos integrados depende de la velocidad del portador, por lo que la baja masa efectiva es la razón fundamental por la que se utilizan GaAs y sus derivados en lugar de Si en aplicaciones de gran ancho de banda como la telefonía celular . ^[15] ${\textstyle {\vec {v}}\;=\;\left\Vert \mu \right\Vert \cdot {\vec {E}}}$ ${\textstyle \left\Vert \mu \right\Vert \;=\;{e\tau }/{\left\Vert m^{*}\right\Vert }}$ ${\textstyle e}$

En abril de 2017, investigadores de la Universidad Estatal de Washington afirmaron haber creado un fluido con masa efectiva negativa dentro de un condensado de Bose-Einstein , mediante la ingeniería de la relación de dispersión . ^[16]

Véase también

Modelos de sólidos y cristales:

• Modelo de unión fuerte
• Modelo de electrón libre
• Modelo de electrón casi libre

Notas al pie

1. Kittel, Introducción a la física del estado sólido , octava edición, páginas 194-196
2. Charles Kittel (1996). op. cit . pag. 202.ISBN​ 978-0-471-11181-8.
3. Green, MA (1990). "Concentración intrínseca, densidades efectivas de estados y masa efectiva en silicio". Journal of Applied Physics . 67 (6): 2944–2954. Bibcode :1990JAP....67.2944G. doi :10.1063/1.345414.
4. "Masa efectiva en semiconductores". Ingeniería eléctrica, informática y energética de la Universidad de Colorado. Archivado desde el original el 20 de octubre de 2017. Consultado el 23 de julio de 2016 .
5. Callaway, Joseph (1976). Teoría cuántica del estado sólido. Academic Press.
6. Grecchi, Vincenzo; Sacchetti, Andrea (2005). "Osciladores Bloch: movimiento de paquetes de ondas". arXiv : quant-ph/0506057 .
7. Chaitanya K. Ullal, Jian Shi y Ravishankar Sundararamana American Journal of Physics 87, 291 (2019); https://doi.org/10.1119/1.5092453
8. Green, MA (1990). "Concentración intrínseca, densidades efectivas de estados y masa efectiva en silicio". Journal of Applied Physics . 67 (6): 2944–2954. Bibcode :1990JAP....67.2944G. doi :10.1063/1.345414.
9. SZ Sze, Física de dispositivos semiconductores , ISBN 0-471-05661-8 . 
10. WA Harrison, Estructura electrónica y propiedades de los sólidos , ISBN 0-486-66021-4 . 
11. Este sitio proporciona las masas efectivas de silicio a diferentes temperaturas.
12. M. Schubert, Elipsometría infrarroja en estructuras de capas de semiconductores: fonones, plasmones y polaritones , ISBN 3-540-23249-4 . 
13. Schubert, M.; Kuehne, P.; Darakchieva, V.; Hofmann, T. (2016). "El efecto Hall óptico: descripción del modelo: tutorial". Revista de la Sociedad Óptica de América A . 33 (8): 1553–68. Bibcode :2016JOSAA..33.1553S. doi :10.1364/JOSAA.33.001553. PMID  27505654.
14. Xing, G. (2017). "Función de aptitud electrónica para el cribado de semiconductores como materiales termoeléctricos". Physical Review Materials . 1 (6): 065405. arXiv : 1708.04499 . Código Bibliográfico :2017PhRvM...1f5405X. doi :10.1103/PhysRevMaterials.1.065405. S2CID  67790664.
15. Silveirinha, MRG; Engheta, N. (2012). "Electrónica de transformación: adaptación de la masa efectiva de los electrones". Physical Review B . 86 (16): 161104. arXiv : 1205.6325 . Código Bibliográfico :2012PhRvB..86p1104S. doi :10.1103/PhysRevB.86.161104.
16. Khamehchi, KA (2017). "Hidrodinámica de masa negativa en un condensado de Bose-Einstein acoplado a giro-órbita". Physical Review Letters . 118 (15): 155301. arXiv : 1612.04055 . Código Bibliográfico :2017PhRvL.118o5301K. doi :10.1103/PhysRevLett.118.155301. PMID  28452531. S2CID  44198065.

Referencias

• Pastori Parravicini, G. (1975). Estados electrónicos y transiciones ópticas en sólidos . Pergamon Press . ISBN 978-0-08-016846-3. Este libro contiene una discusión exhaustiva pero accesible del tema con una amplia comparación entre cálculos y experimentos.
• S. Pekar, El método de masa electrónica efectiva en cristales, Zh. Eksp. Teor. Fiz. 16 , 933 (1946).

Enlaces externos

• Archivo NSM