filtro derivado de m

Tipo de filtro electrónico

Partes de este artículo o sección se basan en el conocimiento del lector de la representación de impedancia compleja de capacitores e inductores y del conocimiento de la representación de señales en el dominio de frecuencia .

Los filtros derivados de m o filtros de tipo m son un tipo de filtro electrónico diseñado utilizando el método de imagen . Fueron inventados por Otto Zobel a principios de la década de 1920. ^[1] Este tipo de filtro fue pensado originalmente para su uso con multiplexación telefónica y fue una mejora del filtro de tipo k constante existente . ^[2] El principal problema que se abordó fue la necesidad de lograr una mejor adaptación del filtro a las impedancias de terminación. En general, todos los filtros diseñados por el método de imagen no logran dar una adaptación exacta, pero el filtro de tipo m es una gran mejora con la elección adecuada del parámetro m. La sección de filtro de tipo m tiene una ventaja adicional en que hay una transición rápida desde la frecuencia de corte de la banda de paso a un polo de atenuación justo dentro de la banda de supresión . A pesar de estas ventajas, existe un inconveniente con los filtros de tipo m; en frecuencias más allá del polo de atenuación, la respuesta comienza a aumentar nuevamente y los tipos m tienen un rechazo de banda de supresión deficiente. Por esta razón, los filtros diseñados utilizando secciones de tipo m a menudo se diseñan como filtros compuestos con una mezcla de secciones de tipo k y tipo m y diferentes valores de m en diferentes puntos para obtener el rendimiento óptimo de ambos tipos. ^[3]

Fondo

Zobel patentó una red de adaptación de impedancia en 1920 ^[5] que, en esencia, utilizaba la topología de lo que ahora se denomina filtros de tipo m, pero Zobel no los denominó como tales ni los analizó mediante el método de imágenes. Esto fue anterior a la publicación de George Campbell de su diseño de tipo k constante en 1922 en el que se basa el filtro de tipo m. ^[6] Zobel publicó la teoría de análisis de imágenes de los filtros de tipo m en 1923. ^[7] Los filtros de tipo M y los filtros diseñados con parámetros de imagen, que alguna vez fueron populares, ahora rara vez se diseñan, habiendo sido reemplazados por métodos de síntesis de redes más avanzados . ^[8]

Derivación

Sección media del filtro general de la serie derivada de m

Sección media del filtro paso bajo en derivación derivada de m.
${\displaystyle C={\frac {L}{R_{0}^{2}}}}$

El bloque de construcción de los filtros derivados de m, como ocurre con todos los filtros de impedancia de imagen, es la red en "L", denominada semisección y compuesta por una impedancia en serie Z y una admitancia en derivación Y. El filtro derivado de m es un derivado del filtro de k constante . El punto de partida del diseño son los valores de Z e Y derivados del prototipo de k constante y están dados por

${\displaystyle k^{2}={\frac {Z}{Y}}}$

donde k es la impedancia nominal del filtro, o R ₀ . El diseñador ahora multiplica Z e Y por una constante arbitraria m (0 < m < 1). Hay dos tipos diferentes de sección derivada de m: serie y derivación. Para obtener la semisección en serie derivada de m, el diseñador determina la impedancia que se debe agregar a 1/mY para hacer que la impedancia de imagen Z_iT sea la misma que la impedancia de imagen de la sección k constante original. A partir de la fórmula general para la impedancia de imagen , se puede demostrar que la impedancia adicional requerida es ^[9]

${\displaystyle {\frac {1-m^{2}}{m}}Z.}$

Para obtener la semisección derivada de m, se añade una admitancia a 1/mZ para que la impedancia de imagen Z sea _iΠigual a la impedancia de imagen de la semisección original. Se puede demostrar que la admitancia adicional requerida es ^[10]

${\displaystyle {\frac {1-m^{2}}{m}}Y.}$

Las disposiciones generales de estos circuitos se muestran en los diagramas de la derecha junto con un ejemplo específico de una sección de paso bajo.

Una consecuencia de este diseño es que la sección media derivada de m coincidirá con una sección de tipo k en un solo lado. Además, una sección de tipo m de un valor de m no coincidirá con otra sección de tipo m de otro valor de m excepto en los lados que ofrecen el Z _idel tipo k. ^[11]

Frecuencia de operación

Para la sección de medio paso bajo que se muestra, la frecuencia de corte del tipo m es la misma que la del tipo k y está dada por

${\displaystyle \omega _{c}={\frac {1}{\sqrt {LC}}}.}$

El polo de atenuación se produce en;

${\displaystyle \omega _{\infty }={\frac {\omega _{c}}{\sqrt {1-m^{2}}}}.}$

De esto se desprende claramente que valores más pequeños de m producirán una frecuencia más cercana a la de corte y, por lo tanto, tendrán un corte más agudo. A pesar de este corte, también acerca la respuesta de banda de rechazo no deseada del tipo m a la frecuencia de corte, lo que dificulta su filtrado con secciones posteriores. El valor de m elegido suele ser un compromiso entre estos requisitos conflictivos. También existe un límite práctico a lo pequeño que puede hacerse m debido a la resistencia inherente de los inductores. Esto tiene el efecto de hacer que el polo de atenuación sea menos profundo (es decir, ya no es un polo genuinamente infinito) y que la pendiente de corte sea menos pronunciada. Este efecto se vuelve más marcado a medida que se acerca a , y deja de haber cualquier mejora en la respuesta con un m de aproximadamente 0,2 o menos. ^{[11] [12] [13]} ${\displaystyle \omega _{\infty }}$ ${\displaystyle \omega _{c}\,\!}$ ${\displaystyle \omega _{\infty }}$ ${\displaystyle \omega _{c}\,\!}$

Impedancia de la imagen

Prototipo derivado de m de filtro de paso bajo en derivación Z _iTm Impedancia de imagen para varios valores de m . Los valores por debajo de la frecuencia de corte se muestran solo para mayor claridad.

Las siguientes expresiones para impedancias de imagen hacen referencia a la sección del prototipo de paso bajo. Están escaladas a la impedancia nominal R ₀ = 1, y las frecuencias en esas expresiones están escaladas a la frecuencia de corte ω _c = 1.

Secciones de la serie

Las impedancias de imagen de la sección en serie están dadas por ^[14]

${\displaystyle Z_{iT}={\sqrt {1-\omega ^{2}}}}$

y es el mismo que el de la sección k constante

${\displaystyle Z_{i\Pi m}={\frac {1-\left(\omega /\omega _{\infty }\right)^{2}}{\sqrt {1-\omega ^{2}}}}.}$

Secciones de derivación

Las impedancias de imagen de la sección de derivación se dan por ^[11]

${\displaystyle Z_{i\Pi }={\frac {1}{\sqrt {1-\omega ^{2}}}}}$

y es el mismo que el de la sección k constante

${\displaystyle Z_{iTm}={\frac {\sqrt {1-\omega ^{2}}}{1-\left(\omega /\omega _{\infty }\right)^{2}}}}$

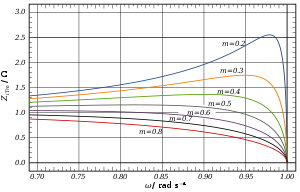
Al igual que en el caso de la sección de tipo k, la impedancia de imagen de la sección de paso bajo de tipo m es puramente real por debajo de la frecuencia de corte y puramente imaginaria por encima de ella. En el gráfico se puede observar que en la banda de paso la coincidencia de impedancia más cercana a una terminación de resistencia pura constante se produce aproximadamente en m = 0,6. ^[14]

Parámetros de transmisión

Función de transferencia de filtro de paso bajo derivada de m para una sola media sección

Para una sección derivada de m en general los parámetros de transmisión para una media sección están dados por ^[14]

${\displaystyle \gamma =\sinh ^{-1}{\frac {mZ}{\sqrt {k^{2}+(1-m^{2})Z^{2}}}}}$

y para n medias secciones

${\displaystyle \gamma _{n}=n\gamma \,\!}$

Para el ejemplo particular de la sección L de paso bajo, los parámetros de transmisión se resuelven de manera diferente en tres bandas de frecuencia. ^[14]

Para que la transmisión no tenga pérdidas: ${\displaystyle 0<\omega <\omega _{c}\,\!}$

${\displaystyle \gamma =\alpha +i\beta =0+i{\frac {1}{2}}\cos ^{-1}\left(1-{\frac {2m^{2}}{\left({\frac {\omega _{c}}{\omega }}\right)^{2}-\left({\frac {\omega _{c}}{\omega _{\infty }}}\right)^{2}}}\right)}$

Para los parámetros de transmisión se encuentran: ${\displaystyle \omega _{c}<\omega <\omega _{\infty }}$

${\displaystyle \gamma =\alpha +i\beta ={\frac {1}{2}}\cosh ^{-1}\left({\frac {2m^{2}}{\left({\frac {\omega _{c}}{\omega }}\right)^{2}-\left({\frac {\omega _{c}}{\omega _{\infty }}}\right)^{2}}}-1\right)+i{\frac {\pi }{2}}}$

Para los parámetros de transmisión se encuentran: ${\displaystyle \omega _{\infty }<\omega <\infty }$

${\displaystyle \gamma =\alpha +i\beta ={\frac {1}{2}}\cosh ^{-1}\left(1-{\frac {2m^{2}}{\left({\frac {\omega _{c}}{\omega }}\right)^{2}-\left({\frac {\omega _{c}}{\omega _{\infty }}}\right)^{2}}}\right)+i0}$

Transformaciones de prototipos

Los gráficos que se muestran de impedancia de imagen, atenuación y cambio de fase son los gráficos de una sección de filtro prototipo de paso bajo . El prototipo tiene una frecuencia de corte de ω _c = 1 rad/s y una impedancia nominal R ₀ = 1 Ω. Esto se produce mediante una sección de filtro a la mitad donde L = 1 henry y C = 1 faradio. Este prototipo puede escalarse en impedancia y frecuencia a los valores deseados. El prototipo de paso bajo también se puede transformar en tipos de paso alto, paso de banda o supresor de banda mediante la aplicación de transformaciones de frecuencia adecuadas . ^[15]

Secciones en cascada

Varias semisecciones L pueden conectarse en cascada para formar un filtro compuesto . En estas combinaciones, la misma impedancia siempre debe estar orientada hacia la misma. Por lo tanto, hay dos circuitos que pueden formarse con dos semisecciones L idénticas. Cuando Z _iTestá orientada hacia Z _iT, la sección se denomina Πsección. Cuando Z _iΠestá orientada hacia Z, _iΠla sección formada es una sección T. La adición de otras semisecciones a cualquiera de estas formas forma una red en escalera que puede comenzar y terminar con elementos en serie o en derivación. ^[16]

Hay que tener en cuenta que las características del filtro predichas por el método de imagen sólo son precisas si la sección termina con su impedancia de imagen. Esto no suele ser así en el caso de las secciones de cada extremo, que suelen terminar con una resistencia fija. Cuanto más alejada esté la sección del extremo del filtro, más precisa será la predicción, ya que los efectos de las impedancias de terminación quedan enmascarados por las secciones intermedias. Es habitual proporcionar medias secciones en los extremos del filtro con m = 0,6, ya que este valor proporciona la Z más plana _ien la banda de paso y, por tanto, la mejor adaptación a una terminación resistiva. ^[17]

Véase también

• Impedancia de la imagen
• Filtro k constante
• Filtros de imagen generales de tipo m _n
• Filtro tipo mm
• Filtro de imagen compuesta

Referencias

1. Belevitch, V , "Resumen de la historia de la teoría de circuitos", Actas del IRE , vol 50 , Iss 5, pp.849, mayo de 1962.
2. Bray, J, Innovación y la revolución de las comunicaciones , p.62, Instituto de Ingenieros Eléctricos, 2002 ISBN  0-85296-218-5 .
3. Zobel, págs. 16-19.
4. Zobel, OJ, Filtros de ondas eléctricas , patente estadounidense 1.850.146 , págs. 2-3, presentada el 25 de noviembre de 1930, expedida el 22 de marzo de 1932.
5. Zobel, OJ, Red de terminación para filtros , patente estadounidense 1.557.229 , presentada el 30 de abril de 1920, emitida el 13 de octubre de 1925.
6. Campbell, GA, "Teoría física del filtro de ondas eléctricas", Bell System Tech J , noviembre de 1922, vol. 1, n.º 2, págs. 1–32.
7. Zobel, OJ, Teoría y diseño de filtros de ondas eléctricas uniformes y compuestos , Bell System Technical Journal, vol. 2 (1923), págs. 1–46.
8. Roberto Sorrentino, Simulación y diseño de filtros electrónicos , pág. 57, McGraw-Hill Professional, 2007 ISBN 0-07-149467-7 . 
9. Matthaei, pág. 64.
10. Matthaei, pág. 66.
11. Matthaei, pág. 65.
12. Bode, Hendrik W., Wave Filter , patente estadounidense 2.002.216 , pág. 1 c. 1 ll.14–26, presentada el 7 de junio de 1933, expedida el 21 de mayo de 1935.
13. Alan Keith Walton, Análisis de redes y práctica , págs. 197, 203, Cambridge University Press, 1987 ISBN 0-521-31903-X . 
14. Matthaei, pág. 63.
15. Matthaei, págs. 60–61 (LPF), 412 (HPF), 438-439 (BPF).
16. Diario de radio de Redifon, 1970 , págs. 45-48, William Collins Sons & Co, 1969.
17. Matthaei, págs. 72–74.

Bibliografía

• Mathaei, Young, Jones Filtros de microondas, redes de adaptación de impedancia y estructuras de acoplamiento McGraw-Hill 1964 (la edición de 1980 es ISBN 0-89006-099-1 ). 
• Para un tratamiento más sencillo del análisis véase,

• Ghosh, Smarajit, Teoría de redes: análisis y síntesis , Prentice Hall of India, págs. 564–569 2005 ISBN 81-203-2638-5 .