
Puntos y cajas es un juego de lápiz y papel para dos jugadores (a veces más). Fue publicado por primera vez en el siglo XIX por el matemático francés Édouard Lucas , quien lo llamó la pipopipette . [1] Ha tenido muchos otros nombres, [2] incluyendo puntos y rayas , juego de puntos , [3] cuadrícula de punto a punto , [4] cajas , [5] y cerdos en un corral . [6]
El juego comienza con una cuadrícula vacía de puntos. Por lo general, dos jugadores se turnan para agregar una sola línea horizontal o vertical entre dos puntos adyacentes no unidos. Un jugador que complete el cuarto lado de una casilla de 1 × 1 gana un punto y juega otro turno. Un punto se registra típicamente colocando una marca que identifica al jugador en la casilla, como una inicial. El juego termina cuando no se pueden colocar más líneas. El ganador es el jugador con más puntos. [2] [7] El tablero puede tener una cuadrícula de cualquier tamaño. Cuando se dispone de poco tiempo o para aprender el juego, es adecuado un tablero de 2 × 2 (3 × 3 puntos). [8] Un tablero de 5 × 5, por otro lado, es bueno para los expertos. [9]
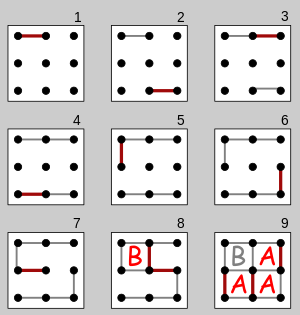
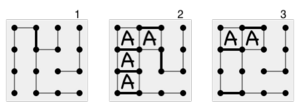
Para la mayoría de los jugadores novatos, el juego comienza con una fase de conexión de puntos más o menos aleatoria, donde la única estrategia es evitar agregar el tercer lado a cualquier casilla. Esto continúa hasta que todas las casillas restantes (potenciales) se unen en cadenas : grupos de una o más casillas adyacentes en los que cualquier movimiento le da todas las casillas de la cadena al oponente. En este punto, los jugadores normalmente toman todas las casillas disponibles y luego abren la cadena más pequeña disponible para su oponente. Por ejemplo, un jugador novato que se enfrenta a una situación como la posición 1 en el diagrama de la derecha, en la que se pueden capturar algunas casillas, puede tomar todas las casillas de la cadena, lo que da como resultado la posición 2. Pero con su último movimiento, tiene que abrir la siguiente cadena, más grande, y el novato pierde el juego. [2] [10]
Un jugador más experimentado que se enfrenta a la posición 1 jugará en cambio la estrategia de la doble traición , tomando todas las cajas menos 2 de la cadena y abandonando la posición 3. El oponente tomará estas dos cajas y luego se verá obligado a abrir la siguiente cadena. Al alcanzar la posición 3, el jugador A gana. La misma estrategia de doble traición se aplica sin importar cuántas cadenas largas haya: un jugador que use esta estrategia tomará todas las cajas menos dos en cada cadena y tomará todas las cajas en la última cadena. Si las cadenas son lo suficientemente largas, entonces este jugador ganará.
El siguiente nivel de complejidad estratégica, entre expertos que utilizarían la estrategia de doble traición (si se les permitiera), es una batalla por el control: un jugador experto intenta obligar a su oponente a abrir la primera cadena larga, porque el jugador que primero abre una cadena larga generalmente pierde. [2] [10] Contra un jugador que no entiende el concepto de sacrificio, el experto simplemente tiene que hacer el número correcto de sacrificios para alentar al oponente a que le entregue la primera cadena lo suficientemente larga para asegurar una victoria. Si el otro jugador también se sacrifica, el experto tiene que manipular adicionalmente el número de sacrificios disponibles a través del juego anterior.
En la teoría de juegos combinatorios , Dots and Boxes es un juego imparcial y muchas posiciones pueden analizarse utilizando la teoría de Sprague-Grundy . Sin embargo, Dots and Boxes carece de la convención de juego normal de la mayoría de los juegos imparciales (donde el último jugador en moverse gana), lo que complica considerablemente el análisis. [2] [10]
No es necesario jugar Dots and Boxes en una cuadrícula rectangular: se puede jugar en una cuadrícula triangular o hexagonal. [2]
Puntos y cajas tiene una forma de gráfico dual llamada "Cadenas y monedas". Este juego se juega en una red de monedas (vértices) unidas por cuerdas (aristas). Los jugadores se turnan para cortar una cuerda. Cuando un corte deja una moneda sin cuerdas, el jugador "embolsa" la moneda y juega otro turno. El ganador es el jugador que embolsa más monedas. Las cadenas y monedas se pueden jugar en un gráfico arbitrario . [2]
En los análisis de Dots and Boxes, un juego que comienza con líneas externas ya dibujadas se llama tablero sueco , mientras que la versión estándar que comienza completamente en blanco se llama tablero americano . Una versión intermedia con solo los lados izquierdo e inferior comenzando con líneas dibujadas se llama tablero islandés . [11]
Un juego relacionado es Dots , que se juega agregando puntos de colores a una cuadrícula en blanco y uniéndolos con líneas rectas o diagonales en un intento de rodear los puntos de un oponente.