punto misiurewicz

Parámetro en el conjunto de Mandelbrot

Una órbita preperiódica.

En matemáticas , un punto de Misiurewicz es un valor de parámetro en el conjunto de Mandelbrot (el espacio de parámetros de aplicaciones cuadráticas complejas ) y también en aplicaciones cuadráticas reales del intervalo ^[1] para las cuales el punto crítico es estrictamente preperiódico (es decir, se convierte en periódica después de un número finito de iteraciones, pero no es periódica en sí misma). Por analogía, el término punto de Misiurewicz también se utiliza para parámetros en un conjunto multibrot donde el punto crítico único es estrictamente preperiódico. Este término tiene menos sentido para mapas en general que tienen más de un punto crítico libre porque algunos puntos críticos pueden ser periódicos y otros no. Estos puntos llevan el nombre del matemático polaco-estadounidense Michał Misiurewicz , quien fue el primero en estudiarlos. ^[2]

Principal Misiurewicz punto del velorio 1/31

Notación matemática

Un parámetro es un punto de Misiurewicz si satisface las ecuaciones: ${\displaystyle c}$ ${\displaystyle M_{k,n}}$

${\displaystyle f_{c}^{(k)}(z_{cr})=f_{c}^{(k+n)}(z_{cr})}$

y:

${\displaystyle f_{c}^{(k-1)}(z_{cr})\neq f_{c}^{(k+n-1)}(z_{cr})}$

entonces:

${\displaystyle M_{k,n}=c:f_{c}^{(k)}(z_{cr})=f_{c}^{(k+n)}(z_{cr})}$

dónde:

• ${\displaystyle z_{cr}}$es un punto crítico de , ${\displaystyle f_{c}}$
• ${\displaystyle k}$y son números enteros positivos, ${\displaystyle n}$
• ${\displaystyle f_{c}^{(k)}}$denota la -ésima iteración de . ${\displaystyle k}$ ${\displaystyle f_{c}}$

Nombre

El término "punto Misiurewicz" se utiliza de manera ambigua: Misiurewicz originalmente investigó mapas en los que todos los puntos críticos no eran recurrentes; es decir, en el que existe una vecindad para cada punto crítico que no es visitado por la órbita de este punto crítico. Este significado está firmemente establecido en el contexto de la dinámica de mapas de intervalos iterados. ^[3] Sólo en casos muy especiales un polinomio cuadrático tiene un punto crítico estrictamente periódico y único. En este sentido restringido, el término se utiliza en dinámica compleja; uno más apropiado serían los puntos de Misiurewicz-Thurston (en honor a William Thurston , quien investigó mapas racionales finitos poscríticamente).

mapas cuadráticos

Un polinomio cuadrático complejo tiene solo un punto crítico. Mediante una conjugación adecuada, cualquier polinomio cuadrático se puede transformar en un mapa de la forma que tiene un único punto crítico en . Los puntos de Misiurewicz de esta familia de mapas son raíces de las ecuaciones: ${\displaystyle P_{c}(z)=z^{2}+c}$ ${\displaystyle z=0}$

${\displaystyle P_{c}^{(k)}(0)=P_{c}^{(k+n)}(0),}$

Sujeto a la condición de que el punto crítico no sea periódico, donde:

• k es el período previo
• n es el periodo
• ${\displaystyle P_{c}^{(n)}=P_{c}(P_{c}^{(n-1)})}$denota la composición n veces de consigo mismo, es decir, la enésima ^iteración de . ${\displaystyle P_{c}(z)=z^{2}+c}$ ${\displaystyle P_{c}}$

Por ejemplo, los puntos de Misiurewicz con k = 2 y n = 1, denotados por M _2,1 , son raíces de:

${\displaystyle {\begin{aligned}&P_{c}^{(2)}(0)=P_{c}^{(3)}(0)\\\Rightarrow {}&c^{2}+c=(c^{2}+c)^{2}+c\\\Rightarrow {}&c^{4}+2c^{3}=0.\end{aligned}}}$

La raíz c = 0 no es un punto de Misiurewicz porque el punto crítico es un punto fijo cuando c = 0, por lo que es periódico en lugar de preperiódico. Esto deja un único punto de Misiurewicz M _2,1 en c = −2.

Propiedades de los puntos de Misiurewicz de mapeo cuadrático complejo

Los puntos de Misiurewicz pertenecen y son densos en el límite del conjunto de Mandelbrot. ^{[4] [5]}

Si es un punto de Misiurewicz, entonces el conjunto de Julia lleno asociado es igual al conjunto de Julia y significa que el conjunto de Julia lleno no tiene interior . ${\displaystyle c}$

Si es un punto de Misiurewicz, entonces en el conjunto de Julia correspondiente todos los ciclos periódicos se repelen (en particular el ciclo en el que cae la órbita crítica). ${\displaystyle c}$

El conjunto de Mandelbrot y el conjunto de Julia son localmente asintóticamente autosimilares alrededor de los puntos de Misiurewicz. ^[6] ${\displaystyle J_{c}}$

Tipos

Los puntos de Misiurewicz en el contexto del conjunto de Mandelbrot se pueden clasificar según varios criterios. Uno de esos criterios es el número de rayos externos que convergen en dicho punto. ^[4] Los puntos de ramificación, que pueden dividir el conjunto de Mandelbrot en dos o más subregiones, tienen tres o más argumentos externos (o ángulos) . Los puntos que no son ramificados tienen exactamente dos rayos externos (estos corresponden a puntos que se encuentran en arcos dentro del conjunto de Mandelbrot). Estos puntos no ramificados son generalmente más sutiles y difíciles de identificar en las representaciones visuales. Los puntos finales, o puntas de las ramas, tienen un solo rayo externo que converge en ellos. Otro criterio para clasificar los puntos de Misiurewicz es su aparición dentro de una gráfica de un subconjunto del conjunto de Mandelbrot. Los puntos de Misiurewicz se pueden encontrar en los centros de las espirales, así como en los puntos donde se encuentran dos o más ramas. ^[7] Según el teorema de rama del conjunto de Mandelbrot, ^[5] todos los puntos de rama del conjunto de Mandelbrot son puntos de Misiurewicz. ^{[4] [5]}

La mayoría de los parámetros de Misiurewicz dentro del conjunto de Mandelbrot exhiben un "centro de espiral". ^[8] Esto ocurre debido al comportamiento en un parámetro de Misiurewicz donde el valor crítico salta a un ciclo periódico repelente después de un número finito de iteraciones. En cada punto del ciclo, el conjunto de Julia exhibe autosemejanza asintótica mediante una multiplicación compleja por la derivada de este ciclo. Si la derivada no es real, implica que el conjunto de Julia cerca del ciclo periódico tiene una estructura en espiral. En consecuencia, se produce una estructura espiral similar en el conjunto de Julia cerca del valor crítico y, según el teorema de Tan Lei , también en el conjunto de Mandelbrot cerca de cualquier parámetro de Misiurewicz para el cual la órbita repelente tiene un multiplicador no real. La visibilidad de la forma de espiral depende del valor de este multiplicador. El número de brazos en la espiral corresponde al número de ramas en el parámetro de Misiurewicz, que a su vez es igual al número de ramas en el valor crítico del conjunto de Julia. Incluso el punto principal de Misiurewicz en la rama de 1/3, ubicado al final de los rayos parámetros en los ángulos 9/56, 11/56 y 15/56, es asintóticamente una espiral con infinitas vueltas, aunque esto es difícil de entender. discernir sin aumento. ^{[ cita necesaria ]}

Argumentos externos

Los argumentos externos de los puntos de Misiurewicz, medidos por turnos son:

• Numeros racionales
• Fracciones propias con denominador par
  • Fracciones diádicas con denominador y expansión finita ( terminal ): ${\displaystyle =2^{b}}$
    $${\displaystyle {\frac {1}{2}}_{10}=0.5_{10}=0.1_{2}}$$
  • Fracciones con denominador y expansión repetida : ^[9] ${\displaystyle =a\cdot 2^{b}}$
    $${\displaystyle {\frac {1}{6}}_{10}={\frac {1}{2\times 3}}_{10}=0.16666..._{10}=0.0(01)..._{2}.}$$

donde: a y b son números enteros positivos y b es impar, el número de subíndice muestra la base del sistema numérico .

Ejemplos de puntos de Misiurewicz de mapeo cuadrático complejo

Puntos finales

Órbita del punto crítico bajo ${\displaystyle z=0}$ ${\displaystyle f_{-2}}$

${\displaystyle c=M_{2,1}}$

El punto se considera un punto final ya que es la punta de un filamento, ^[10] y el punto de aterrizaje del rayo externo para el ángulo 1/6. Su órbita crítica es . ^[11] ${\displaystyle c=M_{2,2}=i}$ ${\displaystyle \{0,i,i-1,-i,i-1,-i...\}}$

El punto se considera un punto final ya que es el punto final de la antena principal del conjunto de Mandelbrot. ^[12] y el punto de aterrizaje de un solo rayo externo (rayo parámetro) de ángulo 1/2. También se considera un punto final porque su órbita crítica es , ^[11] siguiendo la secuencia simbólica = CLRRR... con un preperíodo de 2 y un período de 1. ${\displaystyle c=M_{2,1}=-2}$ ${\displaystyle \{0,-2,2,2,2,...\}}$

Puntos de ramificación

Zoom alrededor del punto principal Misiurewicz durante los períodos del 2 al 1024

${\displaystyle c=M_{4,1}}$

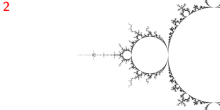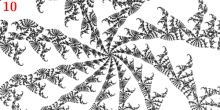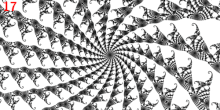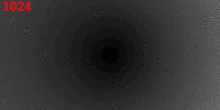
La punta se considera una ramificación porque es una punta principal de Misiurewicz del tercio del limbo y tiene 3 rayos externos: 9/56, 11/56 y 15/56. ${\displaystyle c=-0.10109636384562...+i\,0.95628651080914...=M_{4,1}}$

Otros puntos

Estos son puntos que no son puntos de ramificación ni de fin.

${\displaystyle c=M_{23,2}}$

El punto está cerca de un punto Misiurewicz . Esto se puede ver porque es un centro de una espiral de dos brazos, el punto de aterrizaje de 2 rayos externos con ángulos: y donde está el denominador , y tiene un punto preperiódico con preperíodo y período. ${\displaystyle c=-0.77568377+i\,0.13646737}$ ${\displaystyle M_{23,2}}$ ${\displaystyle {\frac {8388611}{25165824}}}$ ${\displaystyle {\frac {8388613}{25165824}}}$ ${\displaystyle 3*2^{23}}$ ${\displaystyle k=23}$ ${\displaystyle n=2}$

El punto está cerca de un punto de Misiurewicz , ya que es el punto de aterrizaje del par de rayos:, y tiene preperíodo y período . ${\displaystyle c=-1.54368901269109}$ ${\displaystyle M_{3,1}}$ ${\displaystyle {\frac {5}{12}}}$ ${\displaystyle {\frac {7}{12}}}$ ${\displaystyle k=3}$ ${\displaystyle n=1}$

Ver también

• Dinámica aritmética
• Punto de Feigenbaum
• Dendrita (matemáticas)

Referencias

1. Díaz-Ruelas, A.; Baldovín, F.; Robledo, A. (19 de enero de 2022). "Distribuciones de trayectorias de mapas logísticos: grupo de renormalización, entropía y criticidad en la transición al caos". Caos: una revista interdisciplinaria de ciencia no lineal . 31 (3). Caos 31, 033112 (2021): 033112. doi : 10.1063/5.0040544 . hdl : 11577/3387743 . PMID  33810710. S2CID  231933949.
2. Página de inicio de Michał Misiurewicz, Universidad de Indiana-Universidad Purdue de Indianápolis
3. Wellington de Melo, Sebastian van Strien, "Dinámica unidimensional". Monografía, Springer Verlag (1991)
4. Adrien Douady, John Hubbard, "Etude dynamique des polynômes complexes", prépublications mathématiques d'Orsay, 1982/1984
5. Dierk Schleicher, "Sobre fibras y conectividad local de conjuntos de Mandelbrot y Multibrot", en: M. Lapidus, M. van Frankenhuysen (eds): Geometría fractal y aplicaciones: un jubileo de Benoît Mandelbrot. Proceedings of Symposia in Pure Mathematics 72, American Mathematical Society (2004), 477–507 o artículo en línea de arXiv.org
6. Lei.pdf Tan Lei , "Similitud entre el conjunto de Mandelbrot y los conjuntos de Julia", Communications in Mathematical Physics 134 (1990), págs.
7. Geometría fractal Michael Frame de la Universidad de Yale, Benoit Mandelbrot (1924-2010) y Nial Neger 6 de noviembre de 2022
8. El límite del conjunto de Mandelbrot Archivado el 28 de marzo de 2003 en la Wayback Machine por Michael Frame, Benoit Mandelbrot y Nial Neger.
9. Números decimales binarios y números decimales distintos de la base diez por Thomas Kim-wai Yeung y Eric Kin-keung Poon
10. Punta de los filamentos de Robert P. Munafo
11. Puntos preperiódicos (Misiurewicz) en el conjunto de Mandelbrot de Evgeny Demidov
12. punta de las antenas principales por Robert P. Munafo

Otras lecturas

• Michał Misiurewicz (1981), "Medidas absolutamente continuas para ciertos mapas de un intervalo" (en francés). Publicaciones Mathématiques de l'IHÉS, 53 (1981), p. 17-51

enlaces externos

• Puntos preperiódicos (Misiurewicz) en el conjunto de Mandelbrot de Evgeny Demidov
• M & J establece similitud para puntos preperiódicos. Teorema de Lei de Douglas C. Ravenel
• Misiurewicz Punto del mapa logístico por JC Sprott