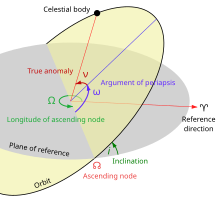
En mecánica celeste , la longitud del periapsis , también llamada longitud del pericentro , de un cuerpo en órbita es la longitud (medida desde el punto del equinoccio de primavera) en la que se produciría el periapsis (el punto de aproximación más cercano al cuerpo central) si la inclinación de la órbita del cuerpo fuera cero. Se suele denotar ϖ .
Para el movimiento de un planeta alrededor del Sol, esta posición se llama longitud del perihelio ϖ, que es la suma de la longitud del nodo ascendente Ω, y el argumento del perihelio ω. [1] [2]
La longitud del periapsis es un ángulo compuesto, en el que una parte se mide en el plano de referencia y el resto en el plano de la órbita . Asimismo, cualquier ángulo derivado de la longitud del periapsis (por ejemplo, la longitud media y la longitud verdadera ) también será compuesto.
A veces, el término longitud del periapsis se utiliza para referirse a ω , el ángulo entre el nodo ascendente y el periapsis. Ese uso del término es especialmente común en discusiones sobre estrellas binarias y exoplanetas. [3] [4] Sin embargo, el ángulo ω se conoce de manera menos ambigua como el argumento del periapsis .
ϖ es la suma de la longitud del nodo ascendente Ω (medida en el plano eclíptico) y el argumento del periapsis ω (medido en el plano orbital):
que se derivan de los vectores de estado orbital .
Defina lo siguiente:
Entonces:
La ascensión recta α y la declinación δ de la dirección del perihelio son:
Si A < 0, agregue 180° a α para obtener el cuadrante correcto.
La longitud eclíptica ϖ y la latitud b del perihelio son:
Si cos(α) < 0, agregue 180° a ϖ para obtener el cuadrante correcto.
A modo de ejemplo, utilizando los números más actualizados de Brown (2017) [5] para el hipotético Planeta Nueve con i = 30°, ω = 136,92° y Ω = 94°, entonces α = 237,38°, δ = +0,41° y ϖ = 235,00°, b = +19,97° (Brown en realidad proporciona i, Ω y ϖ, a partir de los cuales se calculó ω).