En matemáticas , un álgebra de Boole libre es un álgebra de Boole con un conjunto distinguido de elementos, llamados generadores , tales que:
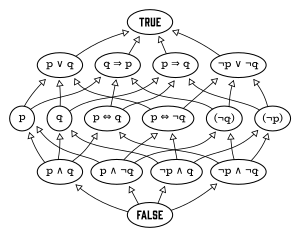
Los generadores de un álgebra de Boole libre pueden representar proposiciones independientes . Consideremos, por ejemplo, las proposiciones "Juan es alto" y "María es rica". Estas generan un álgebra de Boole con cuatro átomos , a saber:
Otros elementos del álgebra de Boole son las disyunciones lógicas de los átomos, como por ejemplo: "Juan es alto y María no es rica, o Juan no es alto y María es rica". Además, hay un elemento más, FALSO, que puede considerarse como la disyunción vacía; es decir, la disyunción de ningún átomo.
Este ejemplo produce un álgebra de Boole con 16 elementos; en general, para n finito , el álgebra de Boole libre con n generadores tiene 2 n átomos y, por lo tanto, elementos.
Si hay un número infinito de generadores , prevalece una situación similar, excepto que ahora no hay átomos . Cada elemento del álgebra de Boole es una combinación de un número finito de proposiciones generadoras, y dos de esos elementos se consideran idénticos si son lógicamente equivalentes .
Otra forma de ver por qué el álgebra booleana libre en un conjunto de n elementos tiene elementos es observar que cada elemento es una función de n bits a uno. Hay posibles entradas para una función de este tipo y la función elegirá 0 o 1 como salida para cada entrada, por lo que hay posibles funciones.
En el lenguaje de la teoría de categorías , las álgebras booleanas libres pueden definirse simplemente en términos de una adjunción entre la categoría de conjuntos y funciones, Set , y la categoría de álgebras booleanas y homomorfismos de álgebras booleanas, BA . De hecho, este enfoque se generaliza a cualquier estructura algebraica definible en el marco del álgebra universal .
Más arriba, dijimos que un álgebra booleana libre es un álgebra booleana con un conjunto de generadores que se comportan de cierta manera; alternativamente, uno podría comenzar con un conjunto y preguntarse qué álgebra genera. Cada conjunto X genera un álgebra booleana libre FX definida como el álgebra tal que para cada álgebra B y función f : X → B , existe un homomorfismo de álgebra booleana único f ′ : FX → B que extiende f . Diagramáticamente ,
donde i X es la inclusión, y la flecha discontinua denota unicidad. La idea es que una vez que uno elige dónde enviar los elementos de X , las leyes para los homomorfismos del álgebra de Boole determinan dónde enviar todo lo demás en el álgebra libre FX . Si FX contuviera elementos inexpresables como combinaciones de elementos de X , entonces f ′ no sería único, y si los elementos de X no fueran suficientemente independientes, entonces f ′ no estaría bien definido. Se muestra fácilmente que FX es único (hasta el isomorfismo), por lo que esta definición tiene sentido. También se muestra fácilmente que un álgebra de Boole libre con conjunto generador X, como se definió originalmente, es isomorfa a FX , por lo que las dos definiciones concuerdan.
Una deficiencia de la definición anterior es que el diagrama no captura que f ′ es un homomorfismo; dado que es un diagrama en Set, cada flecha denota una mera función. Podemos solucionar esto separándolo en dos diagramas, uno en BA y otro en Set . Para relacionar los dos, introducimos un funtor U : BA → Set que " olvida " la estructura algebraica, asignando álgebras y homomorfismos a sus conjuntos y funciones subyacentes.
Si interpretamos la flecha superior como un diagrama en BA y el triángulo inferior como un diagrama en Set , entonces este diagrama expresa correctamente que cada función f : X → UB se extiende a un homomorfismo de álgebra de Boole único f ′ : FX → B . El funtor U puede considerarse como un dispositivo para extraer el homomorfismo f ′ de nuevo hacia Set para que pueda relacionarse con f .
Lo destacable de esto es que el último diagrama es una de las diversas definiciones (equivalentes) de cuándo dos funtores son adjuntos . Nuestro F se extiende fácilmente a un funtor Set → BA , y nuestra definición de X que genera un álgebra booleana libre FX es precisamente que U tiene un adjunto izquierdo F.
El álgebra de Boole libre con generadores κ , donde κ es un número cardinal finito o infinito , puede realizarse como la colección de todos los subconjuntos clopen de {0,1} κ , dada la topología del producto suponiendo que {0,1} tiene la topología discreta . Para cada α<κ, el α ésimo generador es el conjunto de todos los elementos de {0,1} κ cuya α ésima coordenada es 1. En particular, el álgebra de Boole libre con generadores es la colección de todos los subconjuntos clopen de un espacio de Cantor , a veces llamado álgebra de Cantor . Esta colección es contable . De hecho, mientras que el álgebra de Boole libre con n generadores, n finito, tiene cardinalidad , el álgebra de Boole libre con generadores, como para cualquier álgebra libre con generadores y un número contable de operaciones finitas, tiene cardinalidad .
Para obtener más información sobre este enfoque topológico del álgebra de Boole libre, consulte el teorema de representación de Stone para álgebras de Boole .