Suma de prefijo

Secuencia en informática.

En informática , el prefijo suma , suma acumulativa , escaneo inclusivo o simplemente escaneo de una secuencia de números x ₀ , x ₁ , x ₂ , ... es una segunda secuencia de números y ₀ , y ₁ , y ₂ ,. .. , las sumas de prefijos ( totales acumulados ) de la secuencia de entrada:

y ₀ = x ₀

y ₁ = x ₀ + x ₁

y ₂ = x ₀ + x ₁ + x ₂

...

Por ejemplo, las sumas de prefijos de los números naturales son los números triangulares :

Las sumas de prefijos son triviales de calcular en modelos secuenciales de cálculo, utilizando la fórmula y _i = y _{i − 1} + x _i para calcular cada valor de salida en orden secuencial. Sin embargo, a pesar de su facilidad de cálculo, las sumas de prefijos son una primitiva útil en ciertos algoritmos como el ordenamiento por conteo , ^{[1] [2]} y forman la base de la función de escaneo de orden superior en lenguajes de programación funcionales . Las sumas de prefijos también se han estudiado mucho en algoritmos paralelos , tanto como un problema de prueba a resolver como una primitiva útil para usar como subrutina en otros algoritmos paralelos. ^{[3] [4] [5]}

De manera abstracta, una suma de prefijo requiere solo un operador asociativo binario ⊕ , lo que la hace útil para muchas aplicaciones, desde el cálculo de descomposiciones de puntos en pares bien separados hasta el procesamiento de cadenas. ^{[6] [7]}

Matemáticamente, la operación de tomar sumas de prefijos se puede generalizar de secuencias finitas a infinitas; en ese contexto, una suma de prefijo se conoce como suma parcial de una serie . La suma de prefijos o la suma parcial forman operadores lineales en los espacios vectoriales de secuencias finitas o infinitas; sus inversos son operadores en diferencias finitas .

Función de escaneo de orden superior

En términos de programación funcional , la suma del prefijo se puede generalizar a cualquier operación binaria (no solo a la operación de suma ); la función de orden superior resultante de esta generalización se llama escaneo y está estrechamente relacionada con la operación de plegado . Tanto la operación de escaneo como la de plegado aplican la operación binaria dada a la misma secuencia de valores, pero difieren en que el escaneo devuelve la secuencia completa de resultados de la operación binaria, mientras que el plegado devuelve solo el resultado final. Por ejemplo, la secuencia de números factoriales puede generarse mediante una exploración de los números naturales utilizando la multiplicación en lugar de la suma:

Escaneos inclusivos y exclusivos

Las implementaciones de escaneo en lenguajes de programación y bibliotecas pueden ser inclusivas o exclusivas . Un escaneo inclusivo incluye la entrada xi cuando se calcula la salida y _i (es decir, ) mientras _que un escaneo exclusivo no (es decir, ). En el último caso, las implementaciones dejan y ₀ indefinido o aceptan un valor " x ₋₁ " separado con el cual iniciar el escaneo. Cualquier tipo de escaneo se puede transformar en el otro: un escaneo inclusivo se puede transformar en un escaneo exclusivo desplazando la matriz producida por el escaneo hacia la derecha en un elemento e insertando el valor de identidad a la izquierda de la matriz. Por el contrario, un escaneo exclusivo se transforma en un escaneo inclusivo desplazando la matriz producida por el escaneo hacia la izquierda e insertando la suma del último elemento del escaneo y el último elemento de la matriz de entrada a la derecha de la matriz. ^[8] ${\textstyle y_{i}=\bigoplus _{j=0}^{i}x_{j}}$ ${\textstyle y_{i}=\bigoplus _{j=0}^{i-1}x_{j}}$

La siguiente tabla enumera ejemplos de las funciones de escaneo inclusivas y exclusivas proporcionadas por algunos lenguajes y bibliotecas de programación:

El modelo de programación paralela OpenMP basado en directivas admite escaneo inclusivo y exclusivo a partir de la versión 5.0.

Algoritmos paralelos

Existen dos algoritmos clave para calcular una suma de prefijo en paralelo. El primero ofrece un lapso más corto y más paralelismo , pero no es eficiente en el trabajo. El segundo es eficiente en el trabajo pero requiere el doble de tramo y ofrece menos paralelismo. Estos se presentan a su vez a continuación.

Algoritmo 1: tramo más corto, más paralelo

Representación del circuito de una suma de prefijo paralelo de 16 entradas altamente paralela

Hillis y Steele presentan el siguiente algoritmo de suma de prefijos paralelos: ^[9]

para  i <- 0 a piso (log 2 ( n )) hacer  para  j <- 0 a n - 1 hacer en paralelo  si  j < 2 i  entonces  xyo +1 
j<- xyo 
j más  xyo +1 
j<- xyo 
j+ xyo 
j - 2 yo

En lo anterior, la notación significa el valor del jésimo elemento de la matriz x en el paso de tiempo i . ${\displaystyle x_{j}^{i}}$

Con un solo procesador, este algoritmo se ejecutaría en tiempo O ( n log n ) . Sin embargo, si la máquina tiene al menos n procesadores para realizar el bucle interno en paralelo, el algoritmo en su conjunto se ejecuta en tiempo O (log n ) , el número de iteraciones del bucle externo.

Algoritmo 2: trabajo eficiente

Representación de circuito de una suma de prefijo paralelo de 16 entradas eficiente en el trabajo

Se puede calcular una suma de prefijo paralelo eficiente en el trabajo mediante los siguientes pasos. ^{[3] [10] [11]}

1. Calcule las sumas de pares consecutivos de elementos en los que el primer elemento del par tiene un índice par: z ₀ = x ₀ + x ₁ , z ₁ = x ₂ + x ₃ , etc.
2. Calcule recursivamente la suma del prefijo w ₀ , w ₁ , w ₂ , ... de la secuencia z ₀ , z ₁ , z ₂ , ...
3. Expresa cada término de la secuencia final y ₀ , y ₁ , y ₂ , ... como la suma de hasta dos términos de estas secuencias intermedias: y ₀ = x ₀ , y ₁ = z ₀ , y ₂ = z ₀ + x ₂ , y ₃ = w ₁ , etc. Después del primer valor, cada número sucesivo y _i se copia desde una posición a la mitad de la secuencia w , o se agrega el valor anterior a un valor en la secuencia x .

Si la secuencia de entrada tiene n pasos, entonces la recursión continúa hasta una profundidad de O (log n ) , que también es el límite del tiempo de ejecución paralela de este algoritmo. El número de pasos del algoritmo es O ( n ) y se puede implementar en una máquina de acceso aleatorio paralelo con procesadores O ( n /log n ) sin ninguna desaceleración asintótica asignando múltiples índices a cada procesador en rondas del algoritmo para el cual hay más elementos que procesadores. ^[3]

Discusión

Cada uno de los algoritmos anteriores se ejecuta en tiempo O (log n ) . Sin embargo, el primero requiere exactamente log ₂ n pasos, mientras que el segundo requiere 2 log ₂  n − 2 pasos. Para los ejemplos de 16 entradas ilustrados, el algoritmo 1 es paralelo de 12 vías (49 unidades de trabajo divididas por un lapso de 4), mientras que el algoritmo 2 es solo paralelo de 4 vías (26 unidades de trabajo divididas por un lapso de 6). Sin embargo, el algoritmo 2 es eficiente en el trabajo (realiza sólo un factor constante (2) de la cantidad de trabajo requerido por el algoritmo secuencial), mientras que el algoritmo 1 es ineficiente en el trabajo: realiza asintóticamente más trabajo (un factor logarítmico) del requerido. secuencialmente. En consecuencia, es probable que el algoritmo 1 funcione mejor cuando hay abundante paralelismo disponible, pero es probable que el algoritmo 2 funcione mejor cuando el paralelismo es más limitado.

Los algoritmos paralelos para sumas de prefijos a menudo se pueden generalizar a otras operaciones de escaneo en operaciones binarias asociativas , ^{[3] [4]} y también se pueden calcular de manera eficiente en hardware paralelo moderno, como una GPU . ^[12] La idea de construir en hardware una unidad funcional dedicada a calcular la suma de prefijos multiparamétricos fue patentada por Uzi Vishkin . ^[13]

Muchas implementaciones paralelas siguen un procedimiento de dos pasos donde las sumas de prefijos parciales se calculan en el primer paso en cada unidad de procesamiento; luego se calcula la suma del prefijo de estas sumas parciales y se transmite de nuevo a las unidades de procesamiento para una segunda pasada utilizando el prefijo ahora conocido como valor inicial. Asintóticamente, este método requiere aproximadamente dos operaciones de lectura y una operación de escritura por elemento.

Implementaciones concretas de algoritmos de suma de prefijos.

Una implementación de un algoritmo de suma de prefijos paralelos, al igual que otros algoritmos paralelos, debe tener en cuenta la arquitectura de paralelización de la plataforma. Más específicamente, existen múltiples algoritmos que están adaptados para plataformas que trabajan en memoria compartida , así como algoritmos que son muy adecuados para plataformas que usan memoria distribuida , basándose en el paso de mensajes como única forma de comunicación entre procesos.

Memoria compartida: algoritmo de dos niveles

El siguiente algoritmo supone un modelo de máquina de memoria compartida ; todos los elementos de procesamiento (PE) tienen acceso a la misma memoria. Una versión de este algoritmo se implementa en la biblioteca de plantillas estándar de múltiples núcleos (MCSTL), ^{[14] [15]} una implementación paralela de la biblioteca de plantillas estándar de C++ que proporciona versiones adaptadas para la computación paralela de varios algoritmos.

Para calcular simultáneamente la suma del prefijo sobre los elementos de datos con los elementos de procesamiento, los datos se dividen en bloques, cada uno de los cuales contiene elementos (para simplificar, asumimos que se divide ). Tenga en cuenta que, aunque el algoritmo divide los datos en bloques, solo los elementos de procesamiento se ejecutan en paralelo a la vez. ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle p+1}$ ${\displaystyle {\frac {n}{p+1}}}$ ${\displaystyle p+1}$ ${\displaystyle n}$ ${\displaystyle p+1}$ ${\displaystyle p}$

En un primer barrido, cada PE calcula una suma de prefijo local para su bloque. No es necesario calcular el último bloque, ya que estas sumas de prefijos solo se calculan como compensaciones de las sumas de prefijos de los bloques siguientes y, por definición, el último bloque no tiene éxito.

Las compensaciones que se almacenan en la última posición de cada bloque se acumulan en una suma de prefijo propia y se almacenan en sus posiciones siguientes. Para ser un número pequeño, es más rápido hacer esto de forma secuencial, para un número grande , este paso también podría realizarse en paralelo. ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$

Se realiza un segundo barrido. Esta vez no es necesario procesar el primer bloque, ya que no es necesario tener en cuenta el desplazamiento de un bloque anterior. Sin embargo, en este barrido se incluye el último bloque y las sumas de prefijo para cada bloque se calculan teniendo en cuenta las compensaciones de bloque de suma de prefijo calculadas en el barrido anterior.

function suma_prefijo ( elementos ) { n := tamaño ( elementos ) p := número de elementos de procesamiento suma_prefijo := [ 0. . .0 ] de tamaño n hacer paralelo i = 0 a p - 1 { // i := índice del PE actual de j = i * n / ( p + 1 ) a ( i + 1 ) * n / ( p + 1 ) - 1 do { // Esto solo almacena la suma del prefijo de los bloques locales store_prefix_sum_with_offset_in ( elements , 0 , prefix_sum ) } } x = 0 for i = 1 to p { // Acumulación en serie de la suma total de bloques x += prefix_sum [ i * n / ( p + 1 ) - 1 ] // Construye la suma del prefijo sobre los primeros p bloques prefix_sum [ i * n / ( p + 1 )] = x // Guarda los resultados para usarlos como compensaciones en el segundo barrido } hacer paralelo i = 1 a p { // i := índice del PE actual desde j = i * n / ( p + 1 ) a ( i + 1 ) * n / ( p + 1 ) - 1 hacer { offset := prefix_sum [ i * n / ( p + 1 )] // Calcula la suma del prefijo tomando la suma de los bloques anteriores como desplazamiento                                                                                                                        store_prefix_sum_with_offset_in ( elementos , desplazamiento , suma_prefijo ) } } devolver suma_prefijo }       

Mejora: en caso de que la cantidad de bloques sea demasiado grande, lo que hace que el paso en serie requiera mucho tiempo al implementar un solo procesador, se puede usar el algoritmo de Hillis y Steele para acelerar la segunda fase.

Memoria distribuida: algoritmo de hipercubo

El algoritmo de suma de prefijos de hipercubo ^[16] está bien adaptado para plataformas de memoria distribuida y funciona con el intercambio de mensajes entre los elementos de procesamiento. Se supone que los elementos del procesador (PE) que participan en el algoritmo son iguales al número de esquinas en un hipercubo bidimensional . ${\displaystyle p=2^{d}}$ ${\displaystyle d}$

Diferentes hipercubos para diferentes números de nodos.

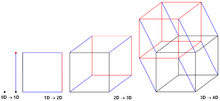
A lo largo del algoritmo, cada PE se ve como una esquina en un hipotético hipercubo con conocimiento de la suma total del prefijo, así como de la suma del prefijo de todos los elementos hasta él mismo (según los índices ordenados entre los PE), ambos en su propio hipercubo. ${\displaystyle \sigma }$ ${\displaystyle x}$

• El algoritmo comienza asumiendo que cada PE es la esquina única de un hipercubo de dimensión cero y, por lo tanto, es igual a la suma del prefijo local de sus propios elementos. ${\displaystyle \sigma }$ ${\displaystyle x}$
• El algoritmo continúa unificando hipercubos adyacentes a lo largo de una dimensión. Durante cada unificación, se intercambia y agrega entre los dos hipercubos, lo que mantiene la invariante de que todos los PE en las esquinas de este nuevo hipercubo almacenan la suma total del prefijo de este hipercubo recién unificado en su variable . Sin embargo, solo el hipercubo que contiene los PE con índice más alto también agrega esto a su variable local , manteniendo el invariante que solo almacena el valor de la suma del prefijo de todos los elementos en los PE con índices menores o iguales a su propio índice. ${\displaystyle \sigma }$ ${\displaystyle \sigma }$ ${\displaystyle \sigma }$ ${\displaystyle x}$ ${\displaystyle x}$

En un hipercubo de dimensión cero con PE en las esquinas, el algoritmo debe repetirse varias veces para que los hipercubos de dimensión cero se unifiquen en un hipercubo unidimensional. Suponiendo un modelo de comunicación dúplex en el que dos PE adyacentes en diferentes hipercubos se pueden intercambiar en ambas direcciones en un solo paso de comunicación, esto significa inicios de comunicación. ${\displaystyle d}$ ${\displaystyle 2^{d}}$ ${\displaystyle d}$ ${\displaystyle 2^{d}}$ ${\displaystyle d}$ ${\displaystyle \sigma }$ ${\displaystyle d=\log _{2}p}$

i := Índice del propio elemento procesador ( PE ) m : = prefijo suma de elementos locales de este PE d : = número de dimensiones del hipercubo                        x = m ; // Invariante: el prefijo suma hasta este PE en el subcubo actual σ = m ; // Invariante: la suma del prefijo de todos los elementos en el subcubo actual      for ( k = 0 ; k <= d - 1 ; k ++ ) { y = σ @ PE ( i xor 2 ^ k ) // Obtener la suma total del prefijo del subcubo opuesto a lo largo de la dimensión k σ = σ + y // Agrega la suma del prefijo de ambos subcubos                     if ( i & 2 ^ k ) { x = x + y // Solo agrega la suma del prefijo del otro subcubo, si este PE es el de índice más alto. } }           

Tamaños de mensajes grandes: árbol binario canalizado

El algoritmo de árbol binario canalizado ^[17] es otro algoritmo para plataformas de memoria distribuida que es específicamente adecuado para mensajes de gran tamaño.

Al igual que el algoritmo del hipercubo, asume una estructura de comunicación especial. Los elementos de procesamiento (PE) están hipotéticamente dispuestos en un árbol binario (por ejemplo, un árbol de Fibonacci) con numeración infija según su índice dentro de los PE. La comunicación en dicho árbol siempre ocurre entre los nodos padre e hijo.

La numeración infija garantiza que para cualquier PE _j dado , los índices de todos los nodos alcanzables por su subárbol izquierdo sean menores que y los índices de todos los nodos en el subárbol derecho sean mayores que . El índice del padre es mayor que cualquiera de los índices en el subárbol de PE _{j si PE j} es un hijo izquierdo y menor si PE _j es un hijo derecho. Esto permite el siguiente razonamiento: ${\displaystyle \mathbb {[l...j-1]} }$ ${\displaystyle j}$ ${\displaystyle \mathbb {[j+1...r]} }$ ${\displaystyle j}$

Intercambio de información entre elementos de procesamiento durante la fase ascendente (azul) y descendente (roja) en el algoritmo de suma de prefijos de árbol binario canalizado.

• La suma del prefijo local del subárbol izquierdo debe agregarse para calcular la suma del prefijo local de PE _j . ${\displaystyle \mathbb {\oplus [l..j-1]} }$ ${\displaystyle \mathbb {\oplus [l..j]} }$
• La suma del prefijo local del subárbol derecho debe agregarse para calcular la suma del prefijo local del PE _h de nivel superior al que se llega en una ruta que contiene una conexión secundaria izquierda (lo que significa ). ${\displaystyle \mathbb {\oplus [j+1..r]} }$ ${\displaystyle h>j}$
• La suma total de prefijos de PE _j es necesaria para calcular las sumas totales de prefijos en el subárbol derecho (por ejemplo, para el nodo de índice más alto del subárbol). ${\displaystyle \mathbb {\oplus [0..j]} }$ ${\displaystyle \mathbb {\oplus [0..j..r]} }$
• PE _j necesita incluir la suma total del prefijo del primer nodo de orden superior al que se llega a través de un camino ascendente que incluye una conexión secundaria derecha para calcular su suma total del prefijo. ${\displaystyle \mathbb {\oplus [0..l-1]} }$

Tenga en cuenta la distinción entre sumas de prefijos totales y locales de subárbol. Los puntos dos, tres y cuatro pueden hacer creer que formarían una dependencia circular, pero no es así. Los PE de nivel inferior pueden requerir la suma total de prefijos de los PE de nivel superior para calcular su suma total de prefijo, pero los PE de nivel superior solo requieren sumas de prefijo local de subárbol para calcular su suma total de prefijo. El nodo raíz como nodo de nivel más alto solo requiere la suma del prefijo local de su subárbol izquierdo para calcular su propia suma de prefijo. Cada PE en la ruta desde PE ₀ hasta la raíz PE solo requiere la suma del prefijo local de su subárbol izquierdo para calcular su propia suma de prefijos, mientras que cada nodo en la ruta desde PE _{p-1 (último PE) hasta la raíz} PE requiere la suma total de prefijo de su padre para calcular su propia suma total de prefijo.

Esto conduce a un algoritmo de dos fases:

Fase ascendente
Propagar la suma del prefijo local del subárbol a su padre para cada PE _j . ${\displaystyle \mathbb {\oplus [l..j..r]} }$

Fase descendente
Propagar la suma total del prefijo exclusivo (PE _j exclusivo , así como los PE en su subárbol izquierdo) de todos los PE de índice inferior que no están incluidos en el subárbol direccionado de PE _j a los PE de nivel inferior en el subárbol secundario izquierdo de PE _j. . Propague la suma del prefijo inclusivo al subárbol secundario derecho de PE _j . ${\displaystyle \mathbb {\oplus [0..l-1]} }$ ${\displaystyle \mathbb {\oplus [0..j]} }$

Tenga en cuenta que el algoritmo se ejecuta en paralelo en cada PE y los PE se bloquearán al recibirlos hasta que sus hijos/padres les proporcionen los paquetes.

k := número de paquetes en un mensaje m de un PE m @ { left , right , parent , this } := // Mensajes en los diferentes PE                  x = m @ esto    // Fase ascendente: calcula las sumas de los prefijos locales del subárbol para j = 0 a k - 1 : // Canalización: para cada paquete de un mensaje si hasLeftChild : bloquea la recepción m [ j ] @ left // Esto reemplaza el m[j] local con el m[j] recibido // Suma agregada de prefijos locales inclusivos de PE de índice inferior x [ j ] = m [ j ] ⨁ x [ j ]                   if hasRightChild : bloqueando recibir m [ j ] @ right // No agregamos m[j] en la suma del prefijo local, ya que los hijos correctos son PE de índice más alto enviar x [ j ] ⨁ m [ j ] al padre else : enviar x [ j ] al padre                  // Fase descendente para j = 0 a k - 1 : m [ j ] @ this = 0         if hasParent : bloqueo de recepción m [ j ] @ parent // Para un hijo izquierdo m[j] es la suma del prefijo exclusivo de los padres, para un hijo derecho la suma del prefijo inclusivo x [ j ] = m [ j ] ⨁ x [ j ] enviar m [ j ] a la izquierda // La suma total del prefijo de todos los PE más pequeños que este o cualquier PE en el subárbol izquierdo enviar x [ j ] a la derecha // La suma total del prefijo de todos los PE más pequeños o iguales que este PE                        

Tubería

Si el mensaje m de longitud n se puede dividir en k paquetes y el operador ⨁ se puede utilizar en cada uno de los paquetes de mensajes correspondientes por separado, es posible la canalización . ^[17]

Si el algoritmo se utiliza sin canalización, siempre hay solo dos niveles (los PE de envío y los PE de recepción) del árbol binario en funcionamiento mientras todos los demás PE están esperando. Si hay p elementos de procesamiento y se utiliza un árbol binario balanceado, el árbol tiene niveles, la longitud del camino desde hasta es por lo tanto el que representa el número máximo de operaciones de comunicación no paralelas durante la fase ascendente, así mismo, la comunicación en la fase descendente El camino también se limita a las startups. Suponiendo un tiempo de inicio de comunicación de y un tiempo de transmisión por bytes de , las fases ascendente y descendente se limitan a un escenario sin canalización. ${\displaystyle \log _{2}p}$ ${\displaystyle PE_{0}}$ ${\displaystyle PE_{\mathbb {root} }}$ ${\displaystyle \log _{2}p-1}$ ${\displaystyle \log _{2}p-1}$ ${\displaystyle T_{\mathbb {start} }}$ ${\displaystyle T_{\mathbb {byte} }}$ ${\displaystyle (2\log _{2}p-2)(T_{\mathbb {start} }+n\cdot T_{\mathbb {byte} })}$

Al dividirlos en k paquetes, cada uno de ellos de tamaño , y enviarlos por separado, el primer paquete aún debe propagarse como parte de una suma de prefijo local y esto ocurrirá nuevamente para el último paquete si . Sin embargo, en el medio, todos los PE a lo largo de la ruta pueden funcionar en paralelo y cada tercera operación de comunicación (recibir a la izquierda, recibir a la derecha, enviar al padre) envía un paquete al siguiente nivel, de modo que se pueda completar una fase en las operaciones de comunicación y Ambas fases juntas necesitan lo cual es favorable para mensajes de gran tamaño n . ${\displaystyle {\tfrac {n}{k}}}$ ${\displaystyle (\log _{2}p-1)\left(T_{\mathbb {start} }+{\frac {n}{k}}\cdot T_{\mathbb {byte} }\right)}$ ${\displaystyle PE_{\mathbb {root} }}$ ${\displaystyle k>\log _{2}p}$ ${\displaystyle 2\log _{2}p-1+3(k-1)}$ ${\displaystyle (4\cdot \log _{2}p-2+6(k-1))\left(T_{\mathbb {start} }+{\frac {n}{k}}\cdot T_{\mathbb {byte} }\right)}$

El algoritmo se puede optimizar aún más haciendo uso de comunicación modelo full-duplex o telefónica y superponiendo la fase ascendente y descendente. ^[17]

Estructuras de datos

Cuando un conjunto de datos puede actualizarse dinámicamente, puede almacenarse en una estructura de datos de árbol de Fenwick . Esta estructura permite tanto la búsqueda de cualquier valor de suma de prefijo individual como la modificación de cualquier valor de matriz en tiempo logarítmico por operación. ^[18] Sin embargo, un artículo anterior de 1982 ^[19] presenta una estructura de datos llamada Árbol de sumas parciales (ver Sección 5.1) que parece superponerse a los árboles de Fenwick; en 1982 el término prefijo-suma aún no era tan común como lo es hoy.

Para matrices de dimensiones superiores, la tabla de áreas sumadas proporciona una estructura de datos basada en sumas de prefijos para calcular sumas de subarreglos rectangulares arbitrarios. Esta puede ser una primitiva útil en operaciones de convolución de imágenes . ^[20]

Aplicaciones

La clasificación por conteo es un algoritmo de clasificación de enteros que utiliza la suma de prefijos de un histograma de frecuencias de claves para calcular la posición de cada clave en la matriz de salida ordenada. Se ejecuta en tiempo lineal para claves enteras que son más pequeñas que la cantidad de elementos y se usa con frecuencia como parte de radix sort , un algoritmo rápido para ordenar números enteros que tienen una magnitud menos restringida. ^[1]

La clasificación de listas , el problema de transformar una lista vinculada en una matriz que representa la misma secuencia de elementos, se puede considerar como calcular una suma de prefijos en la secuencia 1, 1, 1, ... y luego asignar cada elemento a la posición de la matriz. dado por su valor de suma de prefijo; Al combinar clasificación de listas, sumas de prefijos y recorridos de Euler , muchos problemas importantes en los árboles pueden resolverse mediante algoritmos paralelos eficientes. ^[4]

Una de las primeras aplicaciones de los algoritmos de suma de prefijos paralelos fue en el diseño de sumadores binarios , circuitos booleanos que pueden sumar dos números binarios de n bits. En esta aplicación, la secuencia de bits de acarreo de la suma se puede representar como una operación de escaneo sobre la secuencia de pares de bits de entrada, utilizando la función mayoritaria para combinar el acarreo anterior con estos dos bits. Cada bit del número de salida se puede encontrar como exclusivo de dos bits de entrada con el bit de acarreo correspondiente. Al utilizar un circuito que realiza las operaciones del algoritmo de suma de prefijos paralelos, es posible diseñar un sumador que utilice puertas lógicas O ( n ) y pasos de tiempo O (log n ) . ^{[3] [10] [11]}

En el modelo informático de máquina de acceso aleatorio paralelo , las sumas de prefijos se pueden utilizar para simular algoritmos paralelos que asumen la capacidad de que múltiples procesadores accedan a la misma celda de memoria al mismo tiempo, en máquinas paralelas que prohíben el acceso simultáneo. Por medio de una red de clasificación , se puede ordenar un conjunto de solicitudes de acceso a memoria paralelas en una secuencia tal que los accesos a la misma celda sean contiguos dentro de la secuencia; Luego, las operaciones de escaneo se pueden usar para determinar cuál de los accesos tiene éxito al escribir en las celdas solicitadas y para distribuir los resultados de las operaciones de lectura de memoria a múltiples procesadores que solicitan el mismo resultado. ^[21]

En el Ph.D. de Guy Blelloch. tesis, ^[22] las operaciones de prefijo paralelo forman parte de la formalización del modelo de paralelismo de datos proporcionado por máquinas como Connection Machine . Las máquinas de conexión CM-1 y CM-2 proporcionaron una red hipercúbica en la que se podría implementar el algoritmo 1 anterior, mientras que la CM-5 proporcionó una red dedicada para implementar el algoritmo 2. ^[23]

En la construcción de códigos Gray , secuencias de valores binarios con la propiedad de que los valores de secuencia consecutivos difieren entre sí en una posición de un solo bit, un número n se puede convertir en el valor del código Gray en la posición n de la secuencia simplemente tomando el código Gray exclusivo. o de n y n /2 (el número formado al desplazar n hacia la derecha una posición de un solo bit). La operación inversa, decodificar un valor x codificado en Gray en un número binario, es más complicada, pero se puede expresar como la suma del prefijo de los bits de  x , donde cada operación de suma dentro de la suma del prefijo se realiza en módulo dos. Una suma de prefijo de este tipo se puede realizar de manera eficiente utilizando las operaciones booleanas bit a bit disponibles en las computadoras modernas, calculando el o exclusivo de x con cada uno de los números formados desplazando x hacia la izquierda una cantidad de bits que es una potencia de dos. . ^[24]

El prefijo paralelo (usando la multiplicación como operación asociativa subyacente) también se puede usar para construir algoritmos rápidos para la interpolación polinómica paralela . En particular, se puede utilizar para calcular los coeficientes de diferencia dividida de la forma de Newton del polinomio de interpolación. ^[25] Este enfoque basado en prefijos también se puede utilizar para obtener las diferencias divididas generalizadas para la interpolación de Hermite (confluente) , así como para algoritmos paralelos para sistemas de Vandermonde . ^[26]

La suma de prefijo se utiliza para el equilibrio de carga como un algoritmo de bajo costo para distribuir el trabajo entre múltiples procesadores, donde el objetivo primordial es lograr la misma cantidad de trabajo en cada procesador. Los algoritmos utilizan una serie de pesos que representan la cantidad de trabajo requerido para cada elemento. Después de calcular la suma del prefijo, el elemento de trabajo i se envía para su procesamiento a la unidad procesadora con el número . ^[27] Gráficamente esto corresponde a una operación donde la cantidad de trabajo en cada elemento está representada por la longitud de un segmento lineal, todos los segmentos se colocan secuencialmente en una línea y el resultado se corta en un número de piezas, correspondiente al número de procesadores. ^[28] ${\displaystyle [{\frac {prefixSumValue_{i}}{{totalWork}/{numberOfProcessors}}}]}$

Ver también

• Computación de propósito general en unidades de procesamiento de gráficos.
• Escaneo segmentado
• Tabla de áreas sumadas

Referencias

1. Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford (2001), "8.2 Counting Sort", Introducción a los algoritmos (2ª ed.), MIT Press y McGraw-Hill , págs. 168-170, ISBN 0-262-03293-7.
2. Cole, Ricardo; Vishkin, Uzi (1986), "Lanzamiento determinista de monedas con aplicaciones para una clasificación óptima de listas paralelas", Información y control , 70 (1): 32–53, doi : 10.1016/S0019-9958(86)80023-7
3. Ladner, RE; Fischer, MJ (1980), "Computación de prefijos paralelos", Journal of the ACM , 27 (4): 831–838, CiteSeerX 10.1.1.106.6247 , doi :10.1145/322217.322232, MR  0594702, S2CID  207568668 .
4. Tarjan, Robert E .; Vishkin, Uzi (1985), "Un algoritmo eficiente de biconectividad paralela", SIAM Journal on Computing , 14 (4): 862–874, CiteSeerX 10.1.1.465.8898 , doi :10.1137/0214061 .
5. Lakshmivarahan, S.; Dhall, SK (1994), Paralelismo en el problema del prefijo , Oxford University Press , ISBN 0-19508849-2.
6. Blelloch, Guy (2011), Sumas de prefijos y sus aplicaciones (notas de la conferencia) (PDF) , Universidad Carnegie Mellon.
7. Callahan, Pablo; Kosaraju, S. Rao (1995), "Una descomposición de conjuntos de puntos multidimensionales con aplicaciones a k-vecinos más cercanos y n-campos potenciales corporales", Journal of the ACM , 42 (1): 67–90, doi : 10.1145/200836.200853 , S2CID  1818562.
8. "GPU Gems 3".
9. Hillis, W. Daniel; Steele, Jr., Guy L. (diciembre de 1986). "Algoritmos paralelos de datos". Comunicaciones de la ACM . 29 (12): 1170-1183. doi : 10.1145/7902.7903 .
10. Ofman, Yu. (1962), Об алгоритмической сложности funciones de disco, Doklady Akademii Nauk SSSR (en ruso), 145 (1): 48–51, SEÑOR  0168423. Traducción al inglés, "Sobre la complejidad algorítmica de funciones discretas", Física soviética Doklady 7 : 589–591 1963.
11. Khrapchenko, VM (1967), "Estimación asintótica del tiempo de suma de una sumadora paralela", Problemy Kibernet. (en ruso), 19 : 107-122. Traducción al inglés en Syst. Teoría Res. 19 ; 105–122, 1970.
12. Sengupta, Shubhabrata; Harris, Marcos; Zhang, Yao; Owens, John D. (2007). Escanee primitivas para computación GPU. Proc. 22º Simposio ACM SIGGRAPH/EUROGRAPHICS sobre hardware gráfico. págs. 97-106. Archivado desde el original el 3 de septiembre de 2014 . Consultado el 29 de noviembre de 2007 .
13. Vishkin, Uzi (2003). Prefijos de sumas y aplicación de los mismos. Patente estadounidense 6.542.918.
14. Soltero, Johannes. "MCSTL: la biblioteca de plantillas estándar de múltiples núcleos" . Consultado el 29 de marzo de 2019 .
15. Soltero, Johannes; Lijadoras, Peter; Putze, Félix (2007). "MCSTL: la biblioteca de plantillas estándar de múltiples núcleos". Procesamiento paralelo Euro-Par 2007 . Apuntes de conferencias sobre informática. vol. 4641, págs. 682–694. doi :10.1007/978-3-540-74466-5_72. ISBN 978-3-540-74465-8. ISSN  0302-9743.
16. Ananth Grama; Vipin Kumar; Anshul Gupta (2003). Introducción a la Computación Paralela. Addison-Wesley. págs.85, 86. ISBN 978-0-201-64865-2.
17. Sanders, Peter; Träff, Jesper Larsson (2006). "Algoritmos de prefijo paralelo (escaneo) para MPI". Avances recientes en máquinas virtuales paralelas e interfaz de paso de mensajes . Apuntes de conferencias sobre informática. vol. 4192, págs. 49–57. doi :10.1007/11846802_15. ISBN 978-3-540-39110-4. ISSN  0302-9743.
18. Fenwick, Peter M. (1994), "Una nueva estructura de datos para tablas de frecuencia acumulativa", Software: práctica y experiencia , 24 (3): 327–336, doi :10.1002/spe.4380240306, S2CID  7519761
19. Siloé, Yossi; Vishkin, Uzi (1982b), "Un algoritmo de flujo máximo paralelo O ( n ²  log  n )", Journal of Algorithms , 3 (2): 128–146, doi :10.1016/0196-6774(82)90013-X
20. Szeliski, Richard (2010), "Tabla de áreas sumadas (imagen integral)", Visión por computadora: algoritmos y aplicaciones, textos en informática, Springer, págs. 106-107, ISBN 9781848829350.
21. Vishkin, Uzi (1983), "Implementación de acceso simultáneo a direcciones de memoria en modelos que lo prohíben", Journal of Algorithms , 4 (1): 45–50, doi :10.1016/0196-6774(83)90033-0, SEÑOR  0689265.
22. Blelloch, Guy E. (1990). Modelos vectoriales para computación paralela de datos . Cambridge, MA: MIT Press. ISBN 026202313X. OCLC  21761743.
23. Leiserson, Charles E .; Abuhamdeh, Zahi S.; Douglas, David C.; Feynman, Carl R.; Ganmukhi, Mahesh N.; Colina, Jeffrey V.; Hillis, W. Daniel ; Kuszmaul, Bradley C.; St. Pierre, Margaret A. (15 de marzo de 1996). "La Arquitectura de Red de la Máquina de Conexión CM-5". Revista de Computación Paralela y Distribuida . 33 (2): 145-158. doi :10.1006/jpdc.1996.0033. ISSN  0743-7315.
24. Warren, Henry S. (2003), El placer del hacker, Addison-Wesley, pág. 236, ISBN 978-0-201-91465-8.
25. Eğecioğlu, O.; Gallopoulos, E.; Koç, C. (1990), "Un método paralelo para la interpolación rápida y práctica de Newton de alto orden", BIT Computer Science and Numerical Mathematics , 30 (2): 268–288, doi :10.1007/BF02017348, S2CID  9607531.
26. Eğecioğlu, O.; Gallopoulos, E.; Koç, C. (1989), "Cálculo rápido de diferencias divididas e interpolación paralela de Hermite", Journal of Complexity , 5 (4): 417–437, doi :10.1016/0885-064X(89)90018-6
27. Becker, Aarón; Zheng, Gengbin; Kalé, Laxmikant V. (2011). "Equilibrio de carga, memoria distribuida". Enciclopedia de Computación Paralela . Boston, MA: Springer EE. UU. pag. 1046. doi :10.1007/978-0-387-09766-4_504. ISBN 978-0-387-09765-7.
28. Lijadoras, Peter; Mehlhorn, Kurt; Dietzfelbinger, Martín; Dementiev, romano (2019). "Equilibrio de carga" (PDF) . Algoritmos y estructuras de datos secuenciales y paralelos . Cham: Editorial Internacional Springer. pag. 419–434. doi :10.1007/978-3-030-25209-0_14. ISBN 978-3-030-25208-3.

enlaces externos

• Weisstein, Eric W. "Suma acumulada". MundoMatemático .