En geometría diferencial , la segunda forma fundamental (o tensor de forma ) es una forma cuadrática en el plano tangente de una superficie lisa en el espacio euclidiano tridimensional , usualmente denotada por (léase "dos"). Junto con la primera forma fundamental , sirve para definir invariantes extrínsecos de la superficie, sus curvaturas principales . De manera más general, dicha forma cuadrática se define para una subvariedad inmersa lisa en una variedad de Riemann .
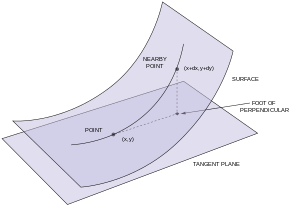
La segunda forma fundamental de una superficie paramétrica S en R 3 fue introducida y estudiada por Gauss . Supongamos primero que la superficie es la gráfica de una función dos veces continuamente diferenciable , z = f ( x , y ) , y que el plano z = 0 es tangente a la superficie en el origen. Entonces f y sus derivadas parciales con respecto a x e y se anulan en (0,0). Por lo tanto, la expansión de Taylor de f en (0,0) comienza con términos cuadráticos:
y la segunda forma fundamental en el origen en las coordenadas ( x , y ) es la forma cuadrática
Para un punto suave P en S , se puede elegir el sistema de coordenadas de manera que el plano z = 0 sea tangente a S en P , y definir la segunda forma fundamental de la misma manera.
La segunda forma fundamental de una superficie paramétrica general se define de la siguiente manera. Sea r = r ( u , v ) una parametrización regular de una superficie en R 3 , donde r es una función de dos variables con valores vectoriales suaves . Es común denotar las derivadas parciales de r con respecto a u y v por r u y r v . La regularidad de la parametrización significa que r u y r v son linealmente independientes para cualquier ( u , v ) en el dominio de r , y por lo tanto abarcan el plano tangente a S en cada punto. De manera equivalente, el producto vectorial r u × r v es un vector distinto de cero normal a la superficie. La parametrización define, por tanto, un campo de vectores normales unitarios n :
La segunda forma fundamental se suele escribir como
su matriz en la base { r u , r v } del plano tangente es
Los coeficientes L , M , N en un punto dado en el plano paramétrico uv están dados por las proyecciones de las segundas derivadas parciales de r en ese punto sobre la línea normal a S y se pueden calcular con la ayuda del producto escalar de la siguiente manera:
Para un campo de distancias con signo de Hessian H , los coeficientes de la segunda forma fundamental se pueden calcular de la siguiente manera:
La segunda forma fundamental de una superficie paramétrica general S se define de la siguiente manera.
Sea r = r ( u 1 , u 2 ) una parametrización regular de una superficie en R 3 , donde r es una función de dos variables con valores vectoriales suaves . Es común denotar las derivadas parciales de r con respecto a u α por r α , α = 1, 2 . La regularidad de la parametrización significa que r 1 y r 2 son linealmente independientes para cualquier ( u 1 , u 2 ) en el dominio de r , y por lo tanto abarcan el plano tangente a S en cada punto. De manera equivalente, el producto vectorial r 1 × r 2 es un vector distinto de cero normal a la superficie. La parametrización define, por tanto, un campo de vectores normales unitarios n :
La segunda forma fundamental se suele escribir como
La ecuación anterior utiliza la convención de suma de Einstein .
Los coeficientes b αβ en un punto dado en el plano paramétrico u 1 u 2 están dados por las proyecciones de las segundas derivadas parciales de r en ese punto sobre la línea normal a S y se pueden calcular en términos del vector normal n de la siguiente manera:
En el espacio euclidiano , la segunda forma fundamental viene dada por
donde es el mapa de Gauss , y la diferencial de considerada como una forma diferencial con valores vectoriales , y los corchetes denotan el tensor métrico del espacio euclidiano.
De manera más general, en una variedad de Riemann, la segunda forma fundamental es una forma equivalente de describir el operador de forma (denotado por S ) de una hipersuperficie,
donde ∇ v w denota la derivada covariante de la variedad ambiental y n un campo de vectores normales en la hipersuperficie. (Si la conexión afín está libre de torsión , entonces la segunda forma fundamental es simétrica).
El signo de la segunda forma fundamental depende de la elección de la dirección de n (lo que se llama coorientación de la hipersuperficie; para las superficies en el espacio euclidiano, esto se da de manera equivalente mediante una elección de la orientación de la superficie).
La segunda forma fundamental se puede generalizar a cualquier codimensión . En ese caso, es una forma cuadrática en el espacio tangente con valores en el fibrado normal y se puede definir por
donde denota la proyección ortogonal de la derivada covariante sobre el fibrado normal.
En el espacio euclidiano , el tensor de curvatura de una subvariedad se puede describir mediante la siguiente fórmula:
Esto se llama ecuación de Gauss , ya que puede verse como una generalización del Teorema Egregium de Gauss .
Para las variedades riemannianas generales hay que añadir la curvatura del espacio ambiente; si N es una variedad embebida en una variedad riemanniana ( M , g ) entonces el tensor de curvatura R N de N con métrica inducida se puede expresar utilizando la segunda forma fundamental y R M , el tensor de curvatura de M :