función monótona

Función matemática que preserva el orden

Figura 1. Una función monótonamente no decreciente

Figura 2. Una función monótonamente no creciente

Figura 3. Una función que no es monótona

En matemáticas , una función monótona (o función monótona ) es una función entre conjuntos ordenados que conserva o invierte el orden dado . ^{[1] [2] [3]} Este concepto surgió por primera vez en el cálculo y luego se generalizó al entorno más abstracto de la teoría del orden .

En cálculo y análisis.

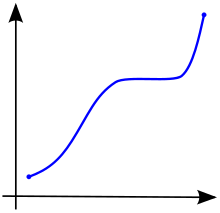
En cálculo , una función definida en un subconjunto de números reales con valores reales se llama monótona si y sólo si es completamente no creciente o completamente no decreciente. ^[2] Es decir, según la Fig. 1, una función que aumenta monótonamente no tiene que aumentar exclusivamente, simplemente no debe disminuir. ${\displaystyle f}$

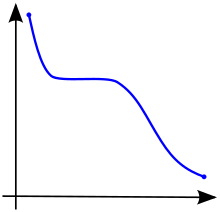
Una función se llama monótonamente creciente (también creciente o no decreciente ) ^[3] si para todos y tales que uno tiene , por lo tanto conserva el orden (ver Figura 1). Asimismo, una función se llama monótonamente decreciente (también decreciente o no creciente ) ^[3] si, siempre que , entonces , entonces invierte el orden (ver Figura 2). ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x\leq y}$ ${\displaystyle f\!\left(x\right)\leq f\!\left(y\right)}$ ${\displaystyle f}$ ${\displaystyle x\leq y}$ ${\displaystyle f\!\left(x\right)\geq f\!\left(y\right)}$

Si el orden en la definición de monotonicidad se reemplaza por el orden estricto , se obtiene un requisito más estricto. Una función con esta propiedad se llama estrictamente creciente (también creciente ). ^{[3] [4]} Nuevamente, al invertir el símbolo de orden, se encuentra un concepto correspondiente llamado estrictamente decreciente (también decreciente ). ^{[3] [4]} Una función con cualquiera de las propiedades se llama estrictamente monótona . Las funciones que son estrictamente monótonas son uno a uno (porque por no igual a , cualquiera o y así, por monotonicidad, cualquiera o , así .) ${\displaystyle \leq }$ ${\displaystyle <}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x<y}$ ${\displaystyle x>y}$ ${\displaystyle f\!\left(x\right)<f\!\left(y\right)}$ ${\displaystyle f\!\left(x\right)>f\!\left(y\right)}$ ${\displaystyle f\!\left(x\right)\neq f\!\left(y\right)}$

Para evitar ambigüedades, los términos débilmente monótono , débilmente creciente y débilmente decreciente se suelen utilizar para referirse a la monotonicidad no estricta.

Los términos "no decreciente" y "no creciente" no deben confundirse con las calificaciones negativas (mucho más débiles) "no decreciente" y "no creciente". Por ejemplo, la función no monótona que se muestra en la figura 3 primero cae, luego aumenta y luego vuelve a caer. Por lo tanto, no es decreciente ni creciente, pero tampoco es no decreciente ni no creciente.

Se dice que una función es absolutamente monótona en un intervalo si las derivadas de todos los órdenes de son no negativas o no positivas en todos los puntos del intervalo. ${\displaystyle f}$ ${\displaystyle \left(a,b\right)}$ ${\displaystyle f}$

Inversa de la función

Todas las funciones estrictamente monótonas son invertibles porque se garantiza que tendrán un mapeo uno a uno desde su rango hasta su dominio.

Sin embargo, las funciones que son sólo débilmente monótonas no son invertibles porque son constantes en algún intervalo (y por lo tanto no son uno a uno).

Una función puede ser estrictamente monótona en un rango limitado de valores y, por lo tanto, tener una inversa en ese rango aunque no sea estrictamente monótona en todas partes. Por ejemplo, si es estrictamente creciente en el rango , entonces tiene una inversa en el rango . ${\displaystyle y=g(x)}$ ${\displaystyle [a,b]}$ ${\displaystyle x=h(y)}$ ${\displaystyle [g(a),g(b)]}$

El término monótono a veces se usa en lugar de estrictamente monótono , por lo que una fuente puede afirmar que todas las funciones monótonas son invertibles cuando en realidad significan que todas las funciones estrictamente monótonas son invertibles. ^{[ cita necesaria ]}

Transformación monótona

El término transformación monótona (o transformación monótona ) también puede causar confusión porque se refiere a una transformación mediante una función estrictamente creciente. Este es el caso en economía con respecto a las propiedades ordinales de una función de utilidad que se conservan a través de una transformada monótona (ver también preferencias monótonas ). ^[5] En este contexto, el término "transformación monótona" se refiere a una transformación monótona positiva y pretende distinguirla de una "transformación monótona negativa", que invierte el orden de los números. ^[6]

Algunas aplicaciones básicas y resultados.

Función monótona con un denso conjunto de discontinuidades de salto (se muestran varias secciones)

Gráficos de 6 funciones de crecimiento monótonas.

Las siguientes propiedades son verdaderas para una función monótona : ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$

• ${\displaystyle f}$tiene límites por la derecha y por la izquierda en cada punto de su dominio ;
• ${\displaystyle f}$tiene un límite en el infinito positivo o negativo ( ) de un número real, o . ${\displaystyle \pm \infty }$ ${\displaystyle \infty }$ ${\displaystyle -\infty }$
• ${\displaystyle f}$sólo puede tener discontinuidades de salto ;
• ${\displaystyle f}$sólo puede tener un número contable de discontinuidades en su dominio. Las discontinuidades, sin embargo, no necesariamente consisten en puntos aislados e incluso pueden ser densas en un intervalo ( a , b ). Por ejemplo, para cualquier secuencia sumable de números positivos y cualquier enumeración de números racionales , la función monótonamente creciente $(a_{i})$ ${\displaystyle (q_{i})}$
  $${\displaystyle f(x)=\sum _{q_{i}\leq x}a_{i}}$$
  es continua exactamente en cada número irracional (ver imagen). Es la función de distribución acumulativa de la medida discreta en los números racionales, donde es el peso de . ${\displaystyle a_{i}}$ ${\displaystyle q_{i}}$

Estas propiedades son la razón por la cual las funciones monótonas son útiles en el trabajo técnico de análisis . Otras propiedades importantes de estas funciones incluyen:

• si es una función monótona definida en un intervalo , entonces es diferenciable en casi todas partes ; es decir , el conjunto de números que no son diferenciables tiene medida de Lebesgue cero . Además, este resultado no se puede mejorar a contable: consulte Función de Cantor . ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle x}$ ${\displaystyle I}$ ${\displaystyle f}$ ${\displaystyle x}$
• si este conjunto es contable, entonces es absolutamente continuo ${\displaystyle f}$
• Si es una función monótona definida en un intervalo , entonces es integrable de Riemann . ${\displaystyle f}$ ${\displaystyle \left[a,b\right]}$ ${\displaystyle f}$

Una aplicación importante de las funciones monótonas es la teoría de la probabilidad . Si es una variable aleatoria , su función de distribución acumulativa es una función monótonamente creciente. ${\displaystyle X}$ ${\displaystyle F_{X}\!\left(x\right)={\text{Prob}}\!\left(X\leq x\right)}$

Una función es unimodal si aumenta monótonamente hasta cierto punto (la moda ) y luego disminuye monótonamente.

Cuando es una función estrictamente monótona , entonces es inyectiva en su dominio, y si es el rango de , entonces hay una función inversa en for . Por el contrario, cada función constante es monótona, pero no inyectiva, ^[7] y por tanto no puede tener una inversa. ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle T}$ ${\displaystyle f}$ ${\displaystyle T}$ ${\displaystyle f}$

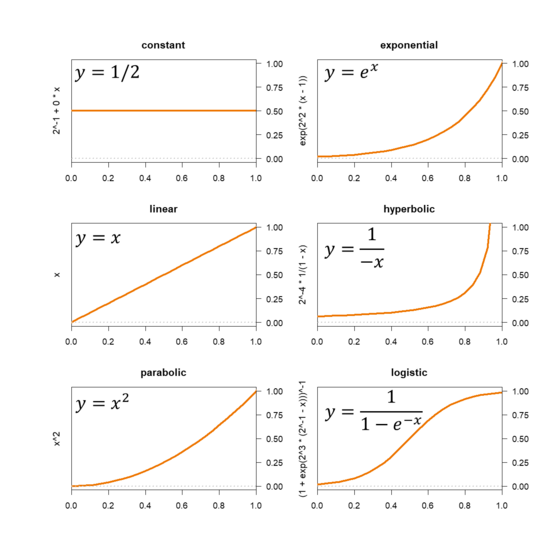
El gráfico muestra seis funciones monótonas. Sus formas más simples se muestran en el área del gráfico y las expresiones utilizadas para crearlas se muestran en el eje y .

En topología

Se dice que un mapa es monótono si cada una de sus fibras está conectada ; es decir, para cada elemento el conjunto (posiblemente vacío) es un subespacio conexo de ${\displaystyle f:X\to Y}$ ${\displaystyle y\in Y,}$ ${\displaystyle f^{-1}(y)}$ ${\displaystyle X.}$

En análisis funcional

En el análisis funcional en un espacio vectorial topológico , se dice que un operador (posiblemente no lineal) es un operador monótono si ${\displaystyle X}$ ${\displaystyle T:X\rightarrow X^{*}}$

$${\displaystyle (Tu-Tv,u-v)\geq 0\quad \forall u,v\in X.}$$

El teorema de Kachurovskiilas funciones convexasespacios de Banach

Se dice que un subconjunto de es monótono si para cada par y en , ${\displaystyle G}$ ${\displaystyle X\times X^{*}}$ ${\displaystyle [u_{1},w_{1}]}$ ${\displaystyle [u_{2},w_{2}]}$ ${\displaystyle G}$

$${\displaystyle (w_{1}-w_{2},u_{1}-u_{2})\geq 0.}$$

${\displaystyle G}$monótono máximomonótono máximoconjunto monótono máximo ${\displaystyle G(T)}$

en teoría del orden

La teoría del orden trata de conjuntos arbitrarios parcialmente ordenados y conjuntos preordenados como una generalización de los números reales. La definición anterior de monotonicidad también es relevante en estos casos. Sin embargo, se evitan los términos "creciente" y "decreciente", ya que su representación pictórica convencional no se aplica a pedidos que no son totales . Además, las relaciones estrictas son de poca utilidad en muchos pedidos no totales y, por tanto, no se introduce terminología adicional para ellas. ${\displaystyle <}$ ${\displaystyle >}$

Denotando la relación de orden parcial de cualquier conjunto parcialmente ordenado, una función monótona , también llamada isótona , o ${\displaystyle \leq }$preservación del orden , satisface la propiedad

$${\displaystyle x\leq y\implies f(x)\leq f(y)}$$

para todo x e y en su dominio. La composición de dos mapeos monótonos también es monótono.

La noción dual suele denominarse antitono , antimonótono o inversión de orden . Por tanto, una función antitono f satisface la propiedad

$${\displaystyle x\leq y\implies f(y)\leq f(x),}$$

para todo x e y en su dominio.

Una función constante es a la vez monótona y antitono; por el contrario, si f es a la vez monótono y antitono, y si el dominio de f es una red , entonces f debe ser constante.

Las funciones monótonas son centrales en la teoría del orden. Aparecen en la mayoría de los artículos sobre el tema y en estos lugares se encuentran ejemplos de aplicaciones especiales. Algunas funciones monótonas especiales notables son las incrustaciones de orden (funciones para las cuales si y solo si y isomorfismos de orden ( incrustaciones de orden sobreyectivas ). ${\displaystyle x\leq y}$ ${\displaystyle f(x)\leq f(y))}$

En el contexto de los algoritmos de búsqueda.

En el contexto de los algoritmos de búsqueda, la monotonicidad (también llamada consistencia) es una condición que se aplica a las funciones heurísticas . Una heurística es monótona si, para cada nodo n y cada sucesor n' de n generado por cualquier acción a , el costo estimado de alcanzar la meta desde n no es mayor que el costo del paso para llegar a n' más el costo estimado de alcanzar el gol de n' , ${\displaystyle h(n)}$

$${\displaystyle h(n)\leq c\left(n,a,n'\right)+h\left(n'\right).}$$

Esta es una forma de desigualdad triangular , con n , n' y el objetivo G _n más cercano a n . Dado que toda heurística monótona también es admisible , la monotonicidad es un requisito más estricto que la admisibilidad. Algunos algoritmos heurísticos como A* pueden resultar óptimos siempre que la heurística que utilizan sea monótona. ^[8]

En funciones booleanas

En álgebra booleana , una función monótona es aquella que para todo a _i y b _i en {0,1} , si a ₁ ≤ b ₁ , a ₂ ≤ b ₂ , ..., a _n ≤ b _n (es decir, la El producto cartesiano {0, 1} ⁿ está ordenado en coordenadas ), entonces f( a ₁ , ..., a _n ) ≤ f( b ₁ , ..., b _n ) . En otras palabras, una función booleana es monótona si, para cada combinación de entradas, cambiar una de las entradas de falsa a verdadera sólo puede hacer que la salida cambie de falsa a verdadera y no de verdadera a falsa. Gráficamente, esto significa que una función booleana n -aria es monótona cuando su representación como un n -cubo etiquetado con valores de verdad no tiene un borde ascendente de verdadero a falso . (Este diagrama de Hasse etiquetado es el dual del diagrama de Venn etiquetado de la función , que es la representación más común para n ≤ 3 ).

Las funciones booleanas monótonas son precisamente aquellas que pueden definirse mediante una expresión que combina las entradas (que pueden aparecer más de una vez) utilizando únicamente los operadores y y o (en particular, no está prohibido). Por ejemplo, "al menos dos de a , b , c se mantienen" es una función monótona de a , b , c , ya que se puede escribir, por ejemplo, como (( a y b ) o ( a y c ) o ( b y c ). )).

El número de funciones de este tipo en n variables se conoce como número de Dedekind de n .

La resolución de SAT , generalmente una tarea NP-difícil , se puede lograr de manera eficiente cuando todas las funciones y predicados involucrados son monótonos y booleanos. ^[9]

Ver también

• Interpolación cúbica monótona
• Operador pseudomonótono
• Coeficiente de correlación de rangos de Spearman : medida de monotonicidad en un conjunto de datos
• monotonicidad total
• Monotonicidad cíclica
• Función monótona del operador
• Función de configuración monótona
• Funciones y secuencias absoluta y completamente monótonas.

Notas

1. Clapham, Cristóbal; Nicholson, James (2014). Diccionario Oxford Conciso de Matemáticas (5ª ed.). Prensa de la Universidad de Oxford.
2. Stover, Christopher. "Función monótona". Wolfram MathWorld . Consultado el 29 de enero de 2018 .
3. "Función monótona". Enciclopedia de Matemáticas . Consultado el 29 de enero de 2018 .
4. Spivak, Michael (1994). Cálculo . Houston, Texas: Publicar o perecer, Inc. p. 192.ISBN​ 0-914098-89-6.
5. Consulte la sección sobre utilidad cardinal versus ordinal en Simon & Blume (1994).
6. Varian, Hal R. (2010). Microeconomía intermedia (8ª ed.). WW Norton & Company. pag. 56.ISBN​ 9780393934243.
7. si su dominio tiene más de un elemento
8. Condiciones de optimización: admisibilidad y coherencia pág. 94–95 (Russell y Norvig, 2010).
9. Sin bahía, Sam; Bayless, Noé; Hoos, Holger H.; Hu, Alan J. (2015). Teorías del módulo monótono del SAT. Proc. 29ª Conferencia AAAI. sobre Inteligencia Artificial. Prensa AAAI. págs. 3702–3709. arXiv : 1406.0043 . doi : 10.1609/aaai.v29i1.9755 . Archivado desde el original el 11 de diciembre de 2023.

Bibliografía

• Bartle, Robert G. (1976). Los elementos del análisis real (segunda ed.).
• Grätzer, George (1971). Teoría de celosías: primeros conceptos y celosías distributivas . ISBN 0-7167-0442-0.
• Pemberton, Malcolm; Rau, Nicolás (2001). Matemáticas para economistas: un libro de texto introductorio . Prensa de la Universidad de Manchester. ISBN 0-7190-3341-1.
• Renardy, Michael y Rogers, Robert C. (2004). Una introducción a las ecuaciones diferenciales parciales . Textos de Matemática Aplicada 13 (Segunda ed.). Nueva York: Springer-Verlag. pag. 356.ISBN​ 0-387-00444-0.
• Riesz, Frigyes y Béla Szőkefalvi-Nagy (1990). Análisis funcional . Publicaciones de Courier Dover. ISBN 978-0-486-66289-3.
• Russell, Stuart J.; Norvig, Peter (2010). Inteligencia artificial: un enfoque moderno (3ª ed.). Upper Saddle River, Nueva Jersey: Prentice Hall. ISBN 978-0-13-604259-4.
• Simón, Carl P.; Blume, Lawrence (abril de 1994). Matemáticas para economistas (primera ed.). ISBN 978-0-393-95733-4.(Definición 9.31)

enlaces externos

• "Función monótona", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Convergencia de una secuencia monótona por Anik Debnath y Thomas Roxlo (The Harker School), Wolfram Demonstrations Project .
• Weisstein, Eric W. "Función monótona". MundoMatemático .