Ciclo de Carnot

Ciclo termodinámico idealizado

Un ciclo de Carnot es un ciclo termodinámico ideal propuesto por el físico francés Sadi Carnot en 1824 y ampliado por otros en las décadas de 1830 y 1840. Según el teorema de Carnot , proporciona un límite superior a la eficiencia de cualquier motor termodinámico clásico durante la conversión de calor en trabajo o, a la inversa, la eficiencia de un sistema de refrigeración al crear una diferencia de temperatura mediante la aplicación de trabajo al sistema.

En un ciclo de Carnot, un sistema o motor transfiere energía en forma de calor entre dos depósitos térmicos a temperaturas y (denominados depósitos caliente y frío, respectivamente), y una parte de esta energía transferida se convierte en trabajo realizado por el sistema. El ciclo es reversible y la entropía se conserva , simplemente se transfiere entre los depósitos térmicos y el sistema sin ganancia ni pérdida. Cuando se aplica trabajo al sistema, el calor se mueve del depósito frío al caliente ( bomba de calor o refrigeración ). Cuando el calor se mueve del depósito caliente al frío, el sistema aplica trabajo al medio ambiente. El trabajo realizado por el sistema o motor al medio ambiente por ciclo de Carnot depende de las temperaturas de los depósitos térmicos y de la entropía transferida del depósito caliente al sistema por ciclo, como , donde es el calor transferido del depósito caliente al sistema por ciclo. ${\displaystyle T_{H}}$ ${\displaystyle T_{C}}$ ${\displaystyle W}$ ${\displaystyle \Delta S}$ ${\displaystyle W=(T_{H}-T_{C})\Delta S=(T_{H}-T_{C}){\frac {Q_{H}}{T_{H}}}}$ ${\displaystyle Q_{H}}$

Etapas

Un ciclo de Carnot como un ciclo termodinámico idealizado realizado por una máquina térmica de Carnot , que consta de los siguientes pasos:

1. 

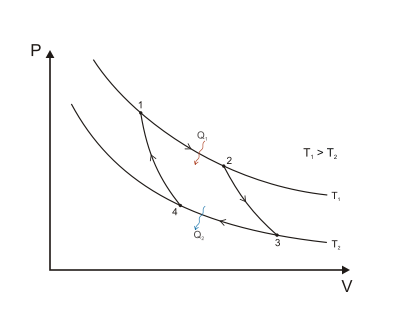
   Expansión isotérmica . El calor (como energía) se transfiere de manera reversible desde el depósito de temperatura caliente a temperatura constante T _H al gas a una temperatura infinitesimalmente menor que T _H . (La diferencia infinitesimal de temperatura permite que el calor se transfiera al gas sin un cambio significativo en la temperatura del gas. Esto se llama adición o absorción de calor isotérmica ). Durante este paso (1 a 2 en la Figura 1 , A a B en la Figura 2 ), el gas está en contacto térmico con el depósito de temperatura caliente y está térmicamente aislado del depósito de temperatura fría. Se permite que el gas se expanda, realizando trabajo sobre los alrededores al empujar hacia arriba el pistón (figura de la Etapa Uno, derecha). Aunque la presión cae de los puntos 1 a 2 (figura 1) la temperatura del gas no cambia durante el proceso porque el calor transferido desde el depósito de temperatura caliente al gas se usa exactamente para realizar trabajo sobre los alrededores por el gas. No hay cambio en la energía interna del gas, y no hay cambio en la temperatura del gas si es un gas ideal. El calor Q _H > 0 se absorbe del depósito de temperatura caliente, lo que da como resultado un aumento de la entropíadel gas en la cantidad. ${\displaystyle S}$ ${\displaystyle \Delta S_{H}=Q_{H}/T_{H}}$

2. 

   Expansión isentrópica ( adiabática reversible ) del gas (salida de trabajo isentrópico). Para este paso (2 a 3 en la Figura 1 , B a C en la Figura 2 ), el gas en el motor está aislado térmicamente de los depósitos caliente y frío, por lo que no ganan ni pierden calor. Es un proceso adiabático . El gas continúa expandiéndose con la reducción de su presión, realizando trabajo sobre los alrededores (elevación del pistón; figura de la Etapa Dos, derecha) y perdiendo una cantidad de energía interna igual al trabajo realizado. La pérdida de energía interna hace que el gas se enfríe. En este paso se enfría a una temperatura que es infinitesimalmente más alta que la temperatura del depósito frío T _C. La entropía permanece inalterada ya que no se transfiere calor Q ( Q = 0) entre el sistema (el gas) y sus alrededores. Es un proceso isentrópico .

3. 

   Compresión isotérmica. El calor se transfiere reversiblemente al depósito de baja temperatura a una temperatura constante T _C (rechazo de calor isotérmico). En este paso (3 a 4 en la Figura 1 , C a D en la Figura 2 ), el gas en el motor está en contacto térmico con el depósito frío a temperatura T _C , y está aislado térmicamente del depósito caliente. La temperatura del gas es infinitesimalmente más alta que T _C para permitir la transferencia de calor del gas al depósito frío. No hay cambio de temperatura, es un proceso isotérmico . Los alrededores realizan trabajo sobre el gas, empujando el pistón hacia abajo (figura de la Etapa Tres, derecha). Una cantidad de energía ganada por el gas de este trabajo se transfiere exactamente como energía térmica Q _C < 0 (negativa como saliendo del sistema, de acuerdo con la convención universal en termodinámica ) al depósito frío por lo que la entropía del sistema disminuye en la cantidad . ^[1] porque la compresión isotérmica disminuye la multiplicidad del gas. ${\displaystyle \Delta S_{C}=Q_{C}/T_{C}}$ ${\displaystyle \Delta S_{C}<0}$

4. 

   Compresión isentrópica. (4 a 1 en la Figura 1 , D a A en la Figura 2 ) Una vez más, el gas en el motor está aislado térmicamente de los depósitos caliente y frío, y se supone que el motor no tiene fricción y que el proceso es lo suficientemente lento, por lo tanto, reversible. Durante este paso, los alrededores realizan trabajo sobre el gas, empujando el pistón hacia abajo aún más (figura de la Etapa Cuatro, derecha), aumentando su energía interna, comprimiéndolo y haciendo que su temperatura vuelva a aumentar a la temperatura infinitesimalmente menor que TH debido únicamente al trabajo agregado al sistema, pero la entropía permanece sin cambios. En este punto _, el gas está en el mismo estado que al comienzo del paso 1.

Figura 1 : Un ciclo de Carnot ilustrado en un diagrama PV para ilustrar el trabajo realizado. 1 a 2 (expansión isotérmica), 2 a 3 (expansión isentrópica), 3 a 4 (compresión isotérmica), 4 a 1 (compresión isentrópica).

En este caso, dado que se trata de un ciclo termodinámico reversible (no hay cambio neto en el sistema y sus alrededores por ciclo) ^{[2] [1]} o, $${\displaystyle \Delta S_{H}+\Delta S_{C}=\Delta S_{\text{cycle}}=0,}$$ $${\displaystyle {\frac {Q_{H}}{T_{H}}}=-{\frac {Q_{C}}{T_{C}}}.}$$

Esto es cierto ya que y son ambos de menor magnitud y, de hecho, están en la misma proporción que . ${\displaystyle Q_{C}}$ ${\displaystyle T_{C}}$ ${\displaystyle Q_{H}/T_{H}}$

El gráfico de presión-volumen

Cuando se representa un ciclo de Carnot en un diagrama de presión-volumen ( Figura 1 ), las etapas isotérmicas siguen las líneas de isoterma del fluido de trabajo, las etapas adiabáticas se mueven entre isotermas y el área delimitada por la trayectoria completa del ciclo representa el trabajo total que se puede realizar durante un ciclo. Del punto 1 al 2 y del punto 3 al 4 la temperatura es constante (proceso isotérmico). La transferencia de calor del punto 4 al 1 y del punto 2 al 3 es igual a cero (proceso adiabático).

Propiedades y significado

El diagrama de temperatura-entropía

Figura 2 : Un ciclo de Carnot como un ciclo termodinámico idealizado realizado por una máquina térmica de Carnot ), ilustrado en un diagrama TS (temperatura T–entropía S). El ciclo tiene lugar entre un depósito caliente a temperatura T _H y un depósito frío a temperatura T _C. El eje vertical es la temperatura del sistema, el eje horizontal es la entropía del sistema. A a B (expansión isotérmica), B a C (expansión isentrópica), C a D (compresión isotérmica), D a A (compresión isentrópica).

Figura 3 : Un ciclo termodinámico generalizado que tiene lugar entre un depósito caliente a temperatura T _H y un depósito frío a temperatura T _C . Por la segunda ley de la termodinámica , el ciclo no puede extenderse fuera de la banda de temperatura de T _C a T _H . El área en rojo, | Q _C |, es la cantidad de energía intercambiada entre el sistema y el depósito frío. El área en blanco, W , es la cantidad de energía de trabajo intercambiada por el sistema con sus alrededores. La cantidad de calor intercambiada con el depósito caliente es la suma de los dos. Si el sistema se comporta como un motor, el proceso se mueve en el sentido de las agujas del reloj alrededor del bucle, y se mueve en el sentido contrario a las agujas del reloj si se comporta como un refrigerador. La eficiencia del ciclo es la relación del área blanca (trabajo) dividida por la suma de las áreas blanca y roja (calor absorbido del depósito caliente).
Q _C (energía perdida en el depósito frío) puede verse como una resta directa, o expresarse como la suma de una cantidad negativa, lo que puede dar lugar a diferentes convenciones.

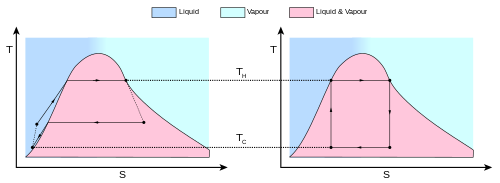
El comportamiento de un motor de Carnot o de un refrigerador se entiende mejor utilizando un diagrama de temperatura-entropía ( diagrama T – S ), en el que el estado termodinámico se especifica mediante un punto en un gráfico con la entropía ( S ) como eje horizontal y la temperatura ( T ) como eje vertical ( Figura 2 ). Para un sistema cerrado simple (análisis de masa de control), cualquier punto en el gráfico representa un estado particular del sistema. Un proceso termodinámico se representa mediante una curva que conecta un estado inicial (A) y un estado final (B). El área bajo la curva es:

que es la cantidad de calor transferido en el proceso. Si el proceso mueve el sistema a una mayor entropía, el área bajo la curva es la cantidad de calor absorbido por el sistema en ese proceso; de lo contrario, es la cantidad de calor eliminado o que sale del sistema. Para cualquier proceso cíclico, hay una parte superior del ciclo y una parte inferior. En los diagramas T - S para un ciclo en el sentido de las agujas del reloj, el área bajo la parte superior será la energía absorbida por el sistema durante el ciclo, mientras que el área bajo la parte inferior será la energía eliminada del sistema durante el ciclo. El área dentro del ciclo es entonces la diferencia entre los dos (la energía térmica neta absorbida), pero como la energía interna del sistema debe haber regresado a su valor inicial, esta diferencia debe ser la cantidad de trabajo realizado por el sistema por ciclo. Refiriéndonos a la Figura 1 , matemáticamente, para un proceso reversible, podemos escribir la cantidad de trabajo realizado durante un proceso cíclico como:

Como dU es una diferencial exacta , su integral sobre cualquier bucle cerrado es cero y se deduce que el área dentro del bucle en un diagrama T – S es (a) igual al trabajo total realizado por el sistema sobre los alrededores si el bucle se recorre en el sentido de las agujas del reloj, y (b) es igual al trabajo total realizado sobre el sistema por los alrededores cuando el bucle se recorre en el sentido contrario a las agujas del reloj.

Figura 4 : Un ciclo de Carnot que tiene lugar entre un depósito caliente a temperatura T _H y un depósito frío a temperatura T _C .

El ciclo de Carnot

Figura 5 : Visualización de un ciclo de Carnot

La evaluación de la integral anterior es particularmente sencilla para un ciclo de Carnot. La cantidad de energía transferida como trabajo es

$${\displaystyle W=\oint PdV=\oint TdS=(T_{H}-T_{C})(S_{B}-S_{A})}$$

La cantidad total de calor transferida desde el depósito caliente al sistema (en la expansión isotérmica) será y la cantidad total de calor transferida desde el sistema al depósito frío (en la compresión isotérmica) será $${\displaystyle Q_{H}=T_{H}(S_{B}-S_{A})=T_{H}\Delta S_{H}}$$ $${\displaystyle Q_{C}=T_{C}(S_{A}-S_{B})=T_{C}\Delta S_{C}<0}$$

Debido a la conservación de la energía, el calor neto transferido, , es igual al trabajo realizado ^[1] ${\displaystyle Q}$ $${\displaystyle W=Q=Q_{H}-Q_{C}}$$

La eficiencia se define como: ${\displaystyle \eta }$

dónde

• W es el trabajo realizado por el sistema (energía que sale del sistema como trabajo),
• ${\displaystyle Q_{C}}$< 0 es el calor extraído del sistema (energía térmica que sale del sistema),
• ${\displaystyle Q_{H}}$> 0 es el calor introducido en el sistema (energía térmica que entra al sistema),
• ${\displaystyle T_{C}}$ es la temperatura absoluta del depósito frío, y
• ${\displaystyle T_{H}}$es la temperatura absoluta del depósito caliente.
• ${\displaystyle S_{B}}$es la entropía máxima del sistema
• ${\displaystyle S_{A}}$es la entropía mínima del sistema

La expresión con la temperatura se puede derivar de las expresiones anteriores con la entropía: y . Como , aparece un signo menos en la expresión final para . ${\displaystyle \eta =1-{\frac {T_{C}}{T_{H}}}}$ ${\displaystyle Q_{H}=T_{H}(S_{B}-S_{A})=T_{H}\Delta S_{H}}$ ${\displaystyle Q_{C}=T_{C}(S_{A}-S_{B})=T_{C}\Delta S_{C}<0}$ ${\displaystyle \Delta S_{C}=S_{A}-S_{B}=-\Delta S_{H}}$ ${\displaystyle \eta }$

Esta es la definición de eficiencia de funcionamiento del motor térmico de Carnot como la fracción del trabajo realizado por el sistema en relación con la energía térmica que recibe el sistema del depósito caliente por ciclo. Esta energía térmica es el iniciador del ciclo.

Ciclo de Carnot invertido

El ciclo de la máquina térmica de Carnot descrito es un ciclo totalmente reversible, es decir, todos los procesos que lo componen pueden invertirse, en cuyo caso se convierte en el ciclo de bomba de calor y refrigeración de Carnot . Esta vez, el ciclo sigue siendo exactamente el mismo, excepto que se invierten las direcciones de las interacciones de calor y trabajo. El calor se absorbe del depósito de baja temperatura, se rechaza hacia un depósito de alta temperatura y se requiere una entrada de trabajo para lograr todo esto. El diagrama P – V del ciclo de Carnot invertido es el mismo que el del ciclo de la máquina térmica de Carnot, excepto que se invierten las direcciones de los procesos. ^[3]

Teorema de Carnot

Se puede ver en el diagrama anterior que para cualquier ciclo que funcione entre temperaturas y , ninguno puede superar la eficiencia de un ciclo de Carnot. ${\displaystyle T_{H}}$ ${\displaystyle T_{C}}$

Figura 6 : Un motor real (izquierda) comparado con el ciclo de Carnot (derecha). La entropía de un material real cambia con la temperatura. Este cambio se indica mediante la curva en un diagrama T – S. Para esta figura, la curva indica un equilibrio vapor-líquido ( ver ciclo de Rankine ). Los sistemas irreversibles y las pérdidas de energía (por ejemplo, trabajo debido a la fricción y pérdidas de calor) impiden que el ideal se produzca en cada paso.

El teorema de Carnot es una declaración formal de este hecho: ningún motor que funcione entre dos depósitos de calor puede ser más eficiente que un motor de Carnot que funcione entre esos mismos depósitos. Por lo tanto, la ecuación 3 da la máxima eficiencia posible para cualquier motor que utilice las temperaturas correspondientes. Un corolario del teorema de Carnot establece que: todos los motores reversibles que funcionan entre los mismos depósitos de calor son igualmente eficientes. Reordenando el lado derecho de la ecuación se obtiene lo que puede ser una forma más fácil de entender de la ecuación, a saber, que la máxima eficiencia teórica de un motor térmico es igual a la diferencia de temperatura entre el depósito caliente y el frío dividida por la temperatura absoluta del depósito caliente. Al observar esta fórmula, se hace evidente un hecho interesante: reducir la temperatura del depósito frío tendrá más efecto en la eficiencia máxima de un motor térmico que aumentar la temperatura del depósito caliente en la misma cantidad. En el mundo real, esto puede ser difícil de lograr, ya que el depósito frío suele ser una temperatura ambiente existente.

En otras palabras, la máxima eficiencia se logra si y solo si la entropía no cambia por ciclo. Se produce un cambio de entropía por ciclo, por ejemplo, si hay fricción que conduce a la disipación de trabajo en calor. En ese caso, el ciclo no es reversible y el teorema de Clausius se convierte en una desigualdad en lugar de una igualdad. De lo contrario, dado que la entropía es una función de estado , el vertido de calor requerido al medio ambiente para eliminar el exceso de entropía conduce a una reducción (mínima) en la eficiencia. Por lo tanto, la ecuación 3 da la eficiencia de cualquier motor térmico reversible .

En los motores térmicos mesoscópicos, el trabajo por ciclo de operación fluctúa en general debido al ruido térmico. Si el ciclo se realiza de forma cuasiestática, las fluctuaciones desaparecen incluso en la mesoescala. ^[4] Sin embargo, si el ciclo se realiza más rápido que el tiempo de relajación del medio de trabajo, las fluctuaciones de trabajo son inevitables. No obstante, cuando se cuentan las fluctuaciones de trabajo y calor, una igualdad exacta relaciona el promedio exponencial del trabajo realizado por cualquier motor térmico con la transferencia de calor desde el baño térmico más caliente. ^[5]

Eficiencia de los motores térmicos reales

Carnot se dio cuenta de que, en realidad, no es posible construir un motor termodinámicamente reversible . Por lo tanto, los motores térmicos reales son incluso menos eficientes que lo que indica la ecuación 3. Además, los motores reales que funcionan según el estilo del ciclo de Carnot (expansión isotérmica / expansión isentrópica / compresión isotérmica / compresión isentrópica) son raros. Sin embargo, la ecuación 3 es extremadamente útil para determinar la eficiencia máxima que podría esperarse para un conjunto dado de depósitos térmicos.

Aunque el ciclo de Carnot es una idealización, la ecuación 3 como expresión de la eficiencia de Carnot sigue siendo útil. Consideremos las temperaturas promedio , en las que la primera integral corresponde a una parte de un ciclo en la que el calor ingresa al sistema y la segunda integral corresponde a una parte del ciclo en la que el calor sale del sistema. Luego, reemplacemos T _H y T _C en la ecuación 3 por ⟨ T _H ⟩ y ⟨ T _C ⟩, respectivamente, para estimar la eficiencia de una máquina térmica. $${\displaystyle \langle T_{H}\rangle ={\frac {1}{\Delta S}}\int _{Q_{\text{in}}}TdS}$$ $${\displaystyle \langle T_{C}\rangle ={\frac {1}{\Delta S}}\int _{Q_{\text{out}}}TdS}$$

Para el ciclo de Carnot, o su equivalente, el valor medio ⟨ T _H ⟩ será igual a la temperatura más alta disponible, es decir, T _H , y ⟨ T _C ⟩ a la más baja, es decir, T _C . Para otros ciclos termodinámicos menos eficientes, ⟨ T _H ⟩ será menor que T _H , y ⟨ T _C ⟩ será mayor que T _C . Esto puede ayudar a ilustrar, por ejemplo, por qué un recalentador o un regenerador puede mejorar la eficiencia térmica de las plantas de energía de vapor y por qué la eficiencia térmica de las plantas de energía de ciclo combinado (que incorporan turbinas de gas que operan a temperaturas aún más altas) supera a la de las plantas de vapor convencionales. El primer prototipo del motor diésel se basó en los principios del ciclo de Carnot.

Como una construcción macroscópica

El motor térmico de Carnot es, en última instancia, una construcción teórica basada en un sistema termodinámico idealizado . A escala humana práctica, el ciclo de Carnot ha demostrado ser un modelo valioso, como en el avance del desarrollo del motor diésel . Sin embargo, a escala macroscópica, las limitaciones impuestas por los supuestos del modelo lo hacen poco práctico y, en última instancia, incapaz de realizar ningún trabajo . ^[6] Como tal, según el teorema de Carnot , el motor de Carnot puede considerarse el límite teórico de los motores térmicos a escala macroscópica en lugar de cualquier dispositivo práctico que pudiera construirse. ^[7]

Véase también

• Motor térmico de Carnot
• Proceso reversible (termodinámica)

Referencias

Notas

1. Planck, M. (1945). "ecuaciones 39, 40 y 65 en las secciones §90 y §137". Tratado de termodinámica. Dover Publications. págs. 75, 135.
2. Fermi, E. (1956). "ecuación 64". Termodinámica (PDF) . Dover Publications. pág. 48.
3. Çengel, Yunus A. y Michael A. Boles. Termodinámica: un enfoque de ingeniería . 7.ª ed. Nueva York: McGraw-Hill, 2011. pág. 299. Impreso.
4. Holubec Viktor y Ryabov Artem (2018). "El ciclismo controla las fluctuaciones de potencia cerca de la eficiencia óptima". Phys. Rev. Lett . 121 (12): 120601. arXiv : 1805.00848 . Código Bibliográfico :2018PhRvL.121l0601H. doi :10.1103/PhysRevLett.121.120601. PMID  30296120. S2CID  52943273.
5. NA Sinitsyn (2011). "Relación de fluctuación para motores térmicos". J. Phys. A: Math. Theor . 44 (40): 405001. arXiv : 1111.7014 . Código Bibliográfico :2011JPhA...44N5001S. doi :10.1088/1751-8113/44/40/405001. S2CID  119261929.
6. Liu, Hang; Meng, Xin-He (18 de agosto de 2017). "Efectos de la energía oscura en la eficiencia de los agujeros negros AdS cargados como motores térmicos". The European Physical Journal C . 77 (8): 556. arXiv : 1704.04363 . doi :10.1140/epjc/s10052-017-5134-9. ISSN  1434-6052. ...desde el motor térmico de Carnot, establecer un límite superior para la eficiencia de un motor térmico es un motor ideal y reversible del cual se debe realizar un solo ciclo en un tiempo infinito, lo que es poco práctico y, por lo tanto, el motor de Carnot tiene potencia cero.
7. Benenti, Giuliano; Casati, Giulio; Wang, Jiao (2020). "Potencia, eficiencia y fluctuaciones en motores térmicos de estado estacionario" (PDF) . Physical Review E. 102 ( 4). Sin embargo, las fluctuaciones [en la temperatura del yacimiento] hacen que estos motores no sean prácticos.

Fuentes

• Carnot, Sadi, Reflexiones sobre la fuerza motriz del fuego
• Ewing, JA (1910) The Steam-Engine and Other Engines edición 3, página 62, vía Internet Archive
• Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (1963). Las conferencias Feynman sobre física . Addison-Wesley Publishing Company. pp. Capítulo 44. ISBN 978-0-201-02116-5.
• Halliday, David; Resnick, Robert (1978). Física (3.ª ed.). John Wiley & Sons. págs. 541–548. ISBN 978-0-471-02456-9.
• Kittel, Charles ; Kroemer, Herbert (1980). Física térmica (2.ª ed.). WH Freeman Company. ISBN 978-0-7167-1088-2.
• Kostic, M (2011). "Revisitando la segunda ley de degradación de energía y generación de entropía: del ingenioso razonamiento de Sadi Carnot a la generalización holística". AIP Conf. Proc . Actas de la conferencia AIP. 1411 (1): 327–350. Bibcode :2011AIPC.1411..327K. CiteSeerX  10.1.1.405.1945 . doi :10.1063/1.3665247.Instituto Americano de Física, 2011. ISBN 978-0-7354-0985-9 . Resumen en: [1]. Artículo completo (24 páginas [2]), también en [3]. 

Enlaces externos

• Artículo de Hyperphysics sobre el ciclo de Carnot.
• Ciclo de Carnot de SM Blinder en gas ideal desarrollado por Wolfram Mathematica