Correlación intraclase

Estadística descriptiva

En estadística , la correlación intraclase o coeficiente de correlación intraclase ( CCI ) ^[1] es una estadística descriptiva que se puede utilizar cuando se realizan mediciones cuantitativas en unidades organizadas en grupos. Describe en qué medida las unidades del mismo grupo se parecen entre sí. Si bien se considera un tipo de correlación , a diferencia de la mayoría de las demás medidas de correlación, opera sobre datos estructurados como grupos en lugar de datos estructurados como observaciones pareadas.

Diagrama de puntos que muestra un conjunto de datos con una alta correlación intraclase. Los valores del mismo grupo tienden a ser similares.

Diagrama de puntos que muestra un conjunto de datos con baja correlación intraclase. Hay muy poca tendencia a que los valores del mismo grupo sean similares.

La correlación intraclase se utiliza habitualmente para cuantificar el grado en el que individuos con un grado fijo de parentesco (por ejemplo, hermanos de sangre entera) se parecen entre sí en términos de un rasgo cuantitativo (véase heredabilidad ). Otra aplicación destacada es la evaluación de la consistencia o reproducibilidad de mediciones cuantitativas realizadas por diferentes observadores que miden la misma cantidad.

Definición temprana de la CCI: fórmula imparcial pero compleja

Los primeros trabajos sobre correlaciones intraclase se centraron en el caso de mediciones pareadas, y las primeras estadísticas de correlación intraclase (ICC) que se propusieron fueron modificaciones de la correlación entre clases (correlación de Pearson).

Considere un conjunto de datos que consta de N valores de datos pareados ( x _{n ,1} ,  x _{n ,2} ), para n  = 1, ..., N . La correlación intraclase r propuesta originalmente ^[2] por Ronald Fisher ^[3] es

${\displaystyle r={\frac {1}{Ns^{2}}}\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}}),}$

dónde

${\displaystyle {\bar {x}}={\frac {1}{2N}}\sum _{n=1}^{N}(x_{n,1}+x_{n,2}),}$

${\displaystyle s^{2}={\frac {1}{2N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}\right\}.}$

Las versiones posteriores de esta estadística ^[3] utilizaron los grados de libertad 2 N  −1 en el denominador para calcular s ² y N  −1 en el denominador para calcular r , de modo que s ² se vuelve insesgado y r se vuelve insesgado si se conoce s .

La diferencia clave entre este ICC y la correlación interclase (Pearson) es que los datos se agrupan para estimar la media y la varianza. La razón de esto es que en el contexto en el que se desea una correlación intraclase, se considera que los pares no están ordenados. Por ejemplo, si estamos estudiando el parecido entre gemelos, normalmente no hay una forma significativa de ordenar los valores de los dos individuos dentro de un par de gemelos. Al igual que la correlación interclase, la correlación intraclase para datos pareados se limitará al intervalo  [−1, +1].

La correlación intraclase también se define para conjuntos de datos con grupos que tienen más de 2 valores. Para grupos que constan de tres valores, se define como ^[3]

${\displaystyle r={\frac {1}{3Ns^{2}}}\sum _{n=1}^{N}\left\{(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}})+(x_{n,1}-{\bar {x}})(x_{n,3}-{\bar {x}})+(x_{n,2}-{\bar {x}})(x_{n,3}-{\bar {x}})\right\},}$

dónde

${\displaystyle {\bar {x}}={\frac {1}{3N}}\sum _{n=1}^{N}(x_{n,1}+x_{n,2}+x_{n,3}),}$

${\displaystyle s^{2}={\frac {1}{3N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,3}-{\bar {x}})^{2}\right\}.}$

A medida que aumenta el número de elementos por grupo, también aumenta el número de términos de productos cruzados en esta expresión. La siguiente forma equivalente es más sencilla de calcular:

${\displaystyle r={\frac {K}{K-1}}\cdot {\frac {N^{-1}\sum _{n=1}^{N}({\bar {x}}_{n}-{\bar {x}})^{2}}{s^{2}}}-{\frac {1}{K-1}},}$

donde K es el número de valores de datos por grupo, y es la media de la muestra del n ^-ésimo grupo. ^[3] Esta forma se atribuye generalmente a Harris . ^[4] El término izquierdo no es negativo; en consecuencia, la correlación intraclase debe satisfacer ${\displaystyle {\bar {x}}_{n}}$

${\displaystyle r\geq {\frac {-1}{K-1}}.}$

Para un valor grande de K , este ICC es casi igual a

${\displaystyle {\frac {N^{-1}\sum _{n=1}^{N}({\bar {x}}_{n}-{\bar {x}})^{2}}{s^{2}}},}$

que puede interpretarse como la fracción de la varianza total que se debe a la variación entre grupos. Ronald Fisher dedica un capítulo entero a la correlación intraclase en su clásico libro Métodos estadísticos para investigadores . ^[3]

Para los datos de una población que es completamente ruidosa, la fórmula de Fisher produce valores de ICC que se distribuyen alrededor de 0, es decir, que a veces son negativos. Esto se debe a que Fisher diseñó la fórmula para que no tuviera sesgos y, por lo tanto, sus estimaciones a veces son sobreestimaciones y a veces subestimaciones. Para valores subyacentes pequeños o cero en la población, el ICC calculado a partir de una muestra puede ser negativo.

Definiciones modernas de la CCI: fórmula más sencilla pero con sesgo positivo

A partir de Ronald Fisher, la correlación intraclase se ha considerado en el marco del análisis de varianza (ANOVA) y, más recientemente, en el marco de los modelos de efectos aleatorios . Se han propuesto varios estimadores de ICC. La mayoría de los estimadores se pueden definir en términos del modelo de efectos aleatorios.

${\displaystyle Y_{ij}=\mu +\alpha _{j}+\varepsilon _{ij},}$

donde Y _ij es la i ^ésima observación en el j ^ésimo grupo, μ es una media global no observada , α _j es un efecto aleatorio no observado compartido por todos los valores en el grupo j y ε _ij es un término de ruido no observado. ^[5] Para que se identifique el modelo, se supone que α _j y ε _ij tienen un valor esperado cero y que no están correlacionados entre sí. Además, se supone que α _j están distribuidos de manera idéntica y que ε _ij están distribuidos de manera idéntica. La varianza de α _j se denota σ^2α
_​y la varianza de ε _ij se denota σ²
_y.

El ICC poblacional en este marco es ^[6]

${\displaystyle {\frac {\sigma _{\alpha }^{2}}{\sigma _{\alpha }^{2}+\sigma _{\varepsilon }^{2}}}.}$

Con este marco, el ICC es la correlación de dos observaciones del mismo grupo.

[Prueba]

Para un modelo de efectos aleatorios unidireccionales:

${\displaystyle Y_{ij}=\mu +\alpha _{i}+\epsilon _{ij}}$

${\displaystyle \alpha _{i}\sim N(0,\sigma _{\alpha }^{2})}$, , s y s son independientes y s son independientes de s. ${\displaystyle \epsilon _{ij}\sim N(0,\sigma _{\varepsilon }^{2})}$ ${\displaystyle \alpha _{i}}$ ${\displaystyle \epsilon _{ij}}$ ${\displaystyle \alpha _{i}}$ ${\displaystyle \epsilon _{ij}}$

La varianza de cualquier observación es: La covarianza de dos observaciones del mismo grupo (para ) es: ^[7] ${\displaystyle Var(Y_{ij})=\sigma _{\varepsilon }^{2}+\sigma _{\alpha }^{2}}$ ${\displaystyle i}$ ${\displaystyle j\neq k}$

${\displaystyle {\begin{aligned}{\text{Cov}}(Y_{ij},Y_{ik})&={\text{Cov}}(\mu +\alpha _{i}+\epsilon _{ij},\mu +\alpha _{i}+\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i}+\epsilon _{ij},\alpha _{i}+\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i},\alpha _{i})+2{\text{Cov}}(\alpha _{i},\epsilon _{ik})+{\text{Cov}}(\epsilon _{ij},\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i},\alpha _{i})\\&={\text{Var}}(\alpha _{i})\\&=\sigma _{\alpha }^{2}.\\\end{aligned}}}$

En esto, hemos utilizado propiedades de la covarianza .

Juntos obtenemos: ${\displaystyle {\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma _{\varepsilon }^{2}+\sigma _{\alpha }^{2}}}}$

Una ventaja de este marco de ANOVA es que los distintos grupos pueden tener distintas cantidades de valores de datos, lo que es difícil de manejar utilizando las estadísticas del ICC anteriores. Este ICC siempre es no negativo, lo que permite interpretarlo como la proporción de la varianza total que se encuentra "entre grupos". Este ICC se puede generalizar para permitir efectos de covariables, en cuyo caso el ICC se interpreta como la captura de la similitud dentro de la clase de los valores de datos ajustados por covariables. ^[8]

Esta expresión nunca puede ser negativa (a diferencia de la fórmula original de Fisher) y, por lo tanto, en muestras de una población que tiene un ICC de 0, los ICC en las muestras serán mayores que el ICC de la población.

Se han propuesto varias estadísticas ICC diferentes, no todas las cuales estiman el mismo parámetro de población. Ha habido un debate considerable sobre qué estadísticas ICC son apropiadas para un uso determinado, ya que pueden producir resultados marcadamente diferentes para los mismos datos. ^{[9] [10]}

Relación con el coeficiente de correlación de Pearson

En términos de su forma algebraica, el ICC original de Fisher es el ICC que más se parece al coeficiente de correlación de Pearson . Una diferencia clave entre las dos estadísticas es que en el ICC, los datos están centrados y escalados utilizando una media y desviación estándar agrupadas, mientras que en la correlación de Pearson, cada variable está centrada y escalada por su propia media y desviación estándar. Esta escala agrupada para el ICC tiene sentido porque todas las mediciones son de la misma cantidad (aunque en unidades de diferentes grupos). Por ejemplo, en un conjunto de datos pareados donde cada "par" es una sola medición realizada para cada una de dos unidades (por ejemplo, pesar a cada gemelo en un par de gemelos idénticos) en lugar de dos mediciones diferentes para una sola unidad (por ejemplo, medir la altura y el peso de cada individuo), el ICC es una medida de asociación más natural que la correlación de Pearson.

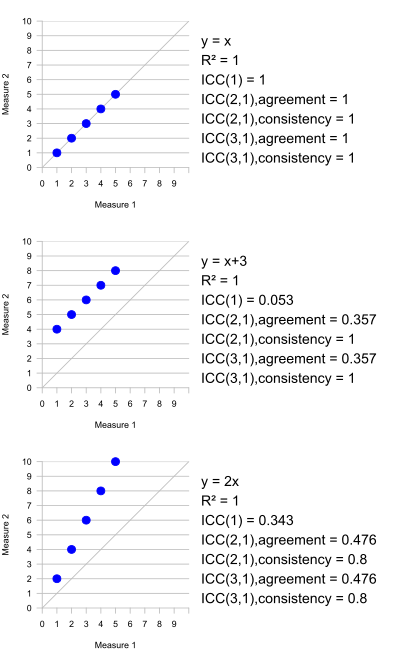
Una propiedad importante de la correlación de Pearson es que es invariante a la aplicación de transformaciones lineales separadas a las dos variables que se comparan. Por lo tanto, si correlacionamos X e Y , donde, digamos, Y  = 2 X  + 1, la correlación de Pearson entre X e Y es 1, una correlación perfecta. Esta propiedad no tiene sentido para el ICC, ya que no hay base para decidir qué transformación se aplica a cada valor de un grupo. Sin embargo, si todos los datos de todos los grupos se someten a la misma transformación lineal, el ICC no cambia.

Uso para evaluar la conformidad entre observadores

El ICC se utiliza para evaluar la consistencia o conformidad de las mediciones realizadas por múltiples observadores que miden la misma cantidad. ^[11] Por ejemplo, si se les pide a varios médicos que califiquen los resultados de una tomografía computarizada para detectar signos de progresión del cáncer, podemos preguntarnos qué tan consistentes son las puntuaciones entre sí. Si se conoce la verdad (por ejemplo, si las tomografías computarizadas se realizaron en pacientes que posteriormente se sometieron a una cirugía exploratoria), entonces el enfoque generalmente se centraría en qué tan bien las puntuaciones de los médicos coincidían con la verdad. Si no se conoce la verdad, solo podemos considerar la similitud entre las puntuaciones. Un aspecto importante de este problema es que existe variabilidad tanto interobservador como intraobservador. La variabilidad interobservador se refiere a las diferencias sistemáticas entre los observadores; por ejemplo, un médico puede puntuar sistemáticamente a los pacientes con un nivel de riesgo más alto que otros médicos. La variabilidad intraobservador se refiere a las desviaciones de la puntuación de un observador particular en un paciente particular que no son parte de una diferencia sistemática.

El ICC está diseñado para ser aplicado a mediciones intercambiables , es decir, datos agrupados en los que no hay una manera significativa de ordenar las mediciones dentro de un grupo. Al evaluar la conformidad entre observadores, si los mismos observadores califican cada elemento que se está estudiando, entonces es probable que existan diferencias sistemáticas entre los observadores, lo que entra en conflicto con la noción de intercambiabilidad. Si el ICC se utiliza en una situación en la que existen diferencias sistemáticas, el resultado es una medida compuesta de variabilidad intraobservador e interobservador. Una situación en la que se podría presumir razonablemente que la intercambiabilidad se cumple sería cuando una muestra que se va a puntuar, por ejemplo una muestra de sangre, se divide en múltiples alícuotas, y las alícuotas se miden por separado en el mismo instrumento. En este caso, la intercambiabilidad se cumpliría siempre que no hubiera ningún efecto debido a la secuencia de análisis de las muestras.

Dado que el coeficiente de correlación intraclase proporciona una combinación de variabilidad intraobservador e interobservador, sus resultados a veces se consideran difíciles de interpretar cuando los observadores no son intercambiables. Se han propuesto medidas alternativas como la estadística kappa de Cohen , la kappa de Fleiss y el coeficiente de correlación de concordancia ^[12] como medidas más adecuadas de acuerdo entre observadores no intercambiables.

Cálculo en paquetes de software

Diferentes definiciones de coeficientes de correlación intraclase aplicadas a tres escenarios de concordancia interobservador.

El paquete de software de código abierto R admite el ICC (utilizando la función "icc" con los paquetes psy o irr, o mediante la función "ICC" en el paquete psych). El paquete rptR ^[13] proporciona métodos para la estimación del ICC y repetibilidades para datos distribuidos por Gauss, binomiales y Poisson en un marco de modelo mixto. En particular, el paquete permite la estimación del ICC ajustado (es decir, controlando otras variables) y calcula intervalos de confianza basados ​​en el bootstrap paramétrico y significancias basadas en la permutación de residuos. El software comercial también admite el ICC, por ejemplo, Stata o SPSS ^[14].

Los tres modelos son:

• Efectos aleatorios unidireccionales: cada sujeto es medido por un conjunto diferente de k evaluadores seleccionados aleatoriamente;
• Aleatorio bidireccional: se seleccionan k evaluadores al azar y luego cada sujeto es medido por el mismo conjunto de k evaluadores;
• Mixto de dos vías: se definen k evaluadores fijos. Cada sujeto es evaluado por los k evaluadores.

Número de medidas:

• Medidas únicas: aunque se tome más de una medida en el experimento, la confiabilidad se aplica a un contexto en el que se realizará una única medida de un único evaluador;
• Medidas promedio: la confiabilidad se aplica a un contexto donde las medidas de k evaluadores se promediarán para cada sujeto.

Coherencia o acuerdo absoluto:

• Acuerdo absoluto: es de interés el acuerdo entre dos evaluadores, incluidos los errores sistemáticos de ambos evaluadores y los errores residuales aleatorios;
• Consistencia: en el contexto de mediciones repetidas por el mismo evaluador, los errores sistemáticos del evaluador se cancelan y solo se mantiene el error residual aleatorio.

La consistencia ICC no se puede estimar en el modelo de efectos aleatorios unidireccional, ya que no hay forma de separar las varianzas interevaluadores y residuales.

Liljequist et al. (2019) también presentaron una descripción general y un nuevo análisis de los tres modelos para el ICC de medidas individuales, con una receta alternativa para su uso. ^[18]

Interpretación

Cicchetti (1994) ^[19] ofrece las siguientes pautas, frecuentemente citadas, para la interpretación de las medidas de acuerdo entre evaluadores kappa o ICC:

• Menos de 0,40: pobre.
• Entre 0,40 y 0,59: aceptable.
• Entre 0,60 y 0,74: bueno.
• Entre 0,75 y 1,00: excelente.

Koo y Li (2016) ofrecen una directriz diferente: ^[20]

• por debajo de 0,50: pobre
• Entre 0,50 y 0,75: moderado
• Entre 0,75 y 0,90: bueno
• por encima de 0,90: excelente

Véase también

• Relación de correlación
• Efecto de diseño
• Tamaño del efecto#Eta-cuadrado (η2)

Referencias

1. Koch GG (1982). "Coeficiente de correlación intraclase". En Samuel Kotz y Norman L. Johnson (ed.). Enciclopedia de ciencias estadísticas . Vol. 4. Nueva York: John Wiley & Sons . págs. 213–217.
2. Bartko JJ (agosto de 1966). "El coeficiente de correlación intraclase como medida de fiabilidad". Psychological Reports . 19 (1): 3–11. doi :10.2466/pr0.1966.19.1.3. PMID  5942109. S2CID  145480729.
3. Fisher RA (1954). Métodos estadísticos para investigadores (duodécima edición). Edimburgo : Oliver y Boyd . ISBN 978-0-05-002170-5.
4. Harris JA (octubre de 1913). "Sobre el cálculo de coeficientes de correlación intraclase e interclase a partir de momentos de clase cuando el número de combinaciones posibles es grande". Biometrika . 9 (3/4): 446–472. doi :10.1093/biomet/9.3-4.446. JSTOR  2331901.
5. Donner A, Koval JJ (marzo de 1980). "La estimación de la correlación intraclase en el análisis de datos familiares". Biometrics . 36 (1): 19–25. doi :10.2307/2530491. JSTOR  2530491. PMID  7370372.
6. Prueba de que el ICC en el modelo anova es la correlación de dos elementos: ocram [1], Entendiendo el coeficiente de correlación intraclase, URL (versión: 2012-12-05): [2]
7. dsaxton (https://stats.stackexchange.com/users/78861/dsaxton), Modelo de efectos aleatorios: las observaciones del mismo nivel tienen covarianza $\sigma^2$?, URL (versión: 2016-03-22) enlace
8. Stanish W, Taylor N (1983). "Estimación del coeficiente de correlación intraclase para el modelo de análisis de covarianza". The American Statistician . 37 (3): 221–224. doi :10.2307/2683375. JSTOR  2683375.
9. Müller R, Büttner P (diciembre de 1994). "Una discusión crítica de los coeficientes de correlación intraclase". Estadísticas en Medicina . 13 (23–24): 2465–76. doi :10.1002/sim.4780132310. PMID  7701147.Ver también el comentario:
   • Vargha P (1997). "Carta al editor". Estadísticas en Medicina . 16 (7): 821–823. doi :10.1002/(SICI)1097-0258(19970415)16:7<821::AID-SIM558>3.0.CO;2-B. PMID  9131768.
10. McGraw KO, Wong SP (1996). "Formación de inferencias sobre algunos coeficientes de correlación intraclase". Psychological Methods . 1 : 30–46. doi :10.1037/1082-989X.1.1.30.Hay varios errores en el artículo:
    • McGraw KO, Wong SP (1996). "Corrección a McGraw y Wong (1996)". Métodos psicológicos . 1 (4): 390. doi :10.1037/1082-989x.1.4.390.
11. Shrout PE, Fleiss JL (marzo de 1979). "Correlaciones intraclase: usos en la evaluación de la fiabilidad del evaluador". Psychological Bulletin . 86 (2): 420–8. doi :10.1037/0033-2909.86.2.420. PMID  18839484.
12. Nickerson CA (diciembre de 1997). "Una nota sobre 'Un coeficiente de correlación de concordancia para evaluar la reproducibilidad'"". Biometría . 53 (4): 1503–1507. doi :10.2307/2533516. JSTOR  2533516.
13. Stoffel MA, Nakagawa S, Schielzeth J (2017). "rptR: estimación de repetibilidad y descomposición de la varianza mediante modelos lineales generalizados de efectos mixtos". Métodos en ecología y evolución . 8 (11): 1639–1644. doi : 10.1111/2041-210x.12797 . ISSN  2041-210X.
14. MacLennan RN (noviembre de 1993). "Confiabilidad entre evaluadores con SPSS para Windows 5.0". The American Statistician . 47 (4): 292–296. doi :10.2307/2685289. JSTOR  2685289.
15. McGraw KO, Wong SP (1996). "Formación de inferencias sobre algunos coeficientes de correlación intraclase". Métodos psicológicos . 1 (1): 30–40. doi :10.1037/1082-989X.1.1.30.
16. Guía del usuario de Stata, versión 15 (PDF) . College Station, Texas: Stata Press. 2017. págs. 1101–1123. ISBN 978-1-59718-249-2.
17. Howell DC. "Coeficientes de correlación intraclase" (PDF) .
18. Liljequist D, Elfving B, Skavberg Roaldsen K (2019). "Correlación intraclase: una discusión y demostración de las características básicas". PLOS ONE . ​​14 (7): e0219854. doi : 10.1371/journal.pone.0219854 . PMC 6645485 . PMID  31329615. 
19. Cicchetti DV (1994). "Directrices, criterios y reglas generales para evaluar instrumentos de evaluación normalizados y estandarizados en psicología". Evaluación psicológica . 6 (4): 284–290. doi :10.1037/1040-3590.6.4.284.
20. Koo TK, Li MY (junio de 2016). "Una guía para seleccionar e informar coeficientes de correlación intraclase para la investigación de confiabilidad". Revista de medicina quiropráctica . 15 (2): 155–63. doi :10.1016/j.jcm.2016.02.012. PMC 4913118 . PMID  27330520. 

Otros

• Comparación de dos índices para el coeficiente de correlación intraclase

Enlaces externos

• AgreeStat 360: análisis de confiabilidad entre evaluadores basado en la nube, kappa de Cohen, AC1/AC2 de Gwet, alfa de Krippendorff, Brennan-Prediger, kappa generalizado de Fleiss, coeficientes de correlación intraclase
• Una útil herramienta en línea que permite calcular los diferentes tipos de ICC