Juego de paridad

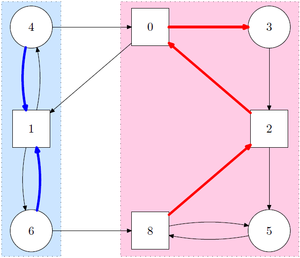
Un juego de paridad se juega en un gráfico dirigido coloreado , donde cada nodo ha sido coloreado por una prioridad, uno de (generalmente) un número finito de números naturales . Dos jugadores, 0 y 1, mueven una ficha (única, compartida) a lo largo de los bordes del gráfico. El propietario del nodo en el que cae la ficha selecciona el nodo sucesor (hace el siguiente movimiento). Los jugadores siguen moviendo la ficha, lo que da como resultado un camino (posiblemente infinito) , llamado jugada.

El ganador de una jugada finita es el jugador cuyo oponente no puede moverse. El ganador de una jugada infinita se determina por las prioridades que aparecen en la jugada. Normalmente, el jugador 0 gana una jugada infinita si la prioridad más alta que aparece infinitamente a menudo en la jugada es par. El jugador 1 gana en caso contrario. Esto explica la palabra "paridad" en el título.

Los juegos de paridad se encuentran en el tercer nivel de la jerarquía de Borel y están determinados en consecuencia . ^[1]

Los juegos relacionados con los juegos de paridad se utilizaron implícitamente en la prueba de decidibilidad de Rabin de la teoría monádica de segundo orden de n sucesores ( S2S para n = 2), donde se demostró la determinación de tales juegos. ^[2] El teorema de Knaster-Tarski conduce a una prueba relativamente simple de determinación de los juegos de paridad. ^[3]

Además, los juegos de paridad no dependen del historial. ^[3]^[4]^[5] Esto significa que si un jugador tiene una estrategia ganadora, entonces ese jugador tiene una estrategia ganadora que depende solo de la posición actual del tablero y no del historial del juego.

Resolver un juego

Problema sin resolver en informática :

¿Es posible resolver juegos de paridad en tiempo polinomial?

(más problemas sin resolver en informática)

Resolver un juego de paridad jugado en un grafo finito significa decidir, para una posición inicial dada, cuál de los dos jugadores tiene una estrategia ganadora. Se ha demostrado que este problema se da en NP y co-NP , más precisamente UP y co-UP, ^[6] así como en QP ( tiempo cuasipolinomial ). ^[7] Sigue siendo una pregunta abierta si este problema de decisión se puede resolver en PTime .

Dado que los juegos de paridad están determinados por la historia, resolver un juego de paridad dado es equivalente a resolver el siguiente problema de teoría de grafos de aspecto simple. Dado un grafo bipartito dirigido y coloreado finito con n vértices y V coloreados con colores de 1 a m , ¿existe una función de elección que seleccione una única arista saliente de cada vértice de , de modo que el subgrafo resultante tenga la propiedad de que en cada ciclo el color más grande que ocurre sea par? $V=V_{0}\cup V_{1}$ ${\estilo de visualización V_{0}}$

Algoritmo recursivo para resolver juegos de paridad

Zielonka describió un algoritmo recursivo que resuelve juegos de paridad. Sea un juego de paridad, donde resp. son los conjuntos de nodos que pertenecen al jugador 0 resp. 1, es el conjunto de todos los nodos, es el conjunto total de aristas y es la función de asignación de prioridad. $G=(V,V_{0},V_{1},E,\Omega)$ ${\estilo de visualización V_{0}}$ $Estilo de visualización V_{1}$ $V=V_{0}\cup V_{1}$ $E\subseteq V\times V$ $\Omega :V\rightarrow \mathbb {N}$

El algoritmo de Zielonka se basa en la notación de atractores. Sea un conjunto de nodos y un jugador. El $i$ -atractor de $U$ es el menor conjunto de nodos que contiene $a U$ de modo que $i$ pueda forzar una visita a $U$ desde cada nodo en . Puede definirse mediante un cálculo de punto fijo: $U\subseteq V$ $i=0,1$ $Attr_{i}(U)$ $Attr_{i}(U)$

{\begin{aligned}Attr_{i}(U)^{0}&:=U\\Attr_{i}(U)^{j+1}&:=Attr_{i}(U)^{j}\cup \{v\in V_{i}\mid \exists (v,w)\in E:w\in Attr_{i}(U)^{j}\}\cup \{v\in V_{1-i}\mid \forall (v,w)\in E:w\in Attr_{i}(U)^{j}\}\\Attr_{i}(U)&:=\bigcup _{j=0}^{\infty }Attr_{i}(U)^{j}\end{aligned}}

En otras palabras, se comienza con el conjunto inicial $U$ . Luego, para cada paso ( ) se suman todos los nodos pertenecientes al jugador 0 que pueden alcanzar el conjunto anterior ( ) con una sola arista y todos los nodos pertenecientes al jugador 1 que deben alcanzar el conjunto anterior ( ) sin importar qué arista tome el jugador 1. $Attr_{i}(U)^{j+1}$ $Attr_{i}(U)^{j}$ $Attr_{i}(U)^{j}$

El algoritmo de Zielonka se basa en un descenso recursivo sobre el número de prioridades. Si la prioridad máxima es 0, es inmediato ver que el jugador 0 gana todo el juego (con una estrategia arbitraria). De lo contrario, sea $p$ el mayor y sea el jugador asociado con la prioridad. Sea el conjunto de nodos con prioridad $p$ y sea el atractor correspondiente del jugador $i$ . El jugador $i$ ahora puede asegurarse de que cada jugada que visita $A$ infinitas veces la gane el jugador $i$ . $i=p{\bmod {2}}$ $U=\{v\mid \Omega (v)=p\}$ $A=Attr_{i}(U)$

Consideremos el juego en el que se eliminan todos los nodos y las aristas afectadas de $A.$ Ahora podemos resolver el juego más pequeño mediante recursión y obtener un par de conjuntos ganadores . Si está vacío, entonces también lo está para el juego $G$ , porque el jugador solo puede decidir escapar de A $,$ lo que también resulta en una victoria para el jugador $i$ . $G'=G\setmenos A$ ${\estilo de visualización G'}$ $W'_{i},W'_{1-i}$ $Estilo de visualización W'_{1-i}}$ $Estilo de visualización W_{1-i}}$ ${\estilo de visualización 1-i}$ $Estilo de visualización W_i$

De lo contrario, si no está vacío, solo sabemos con seguridad que el jugador puede ganar en ya que el jugador $i$ no puede escapar de a $A$ (ya que $A$ es un $i$ -atractor). Por lo tanto, calculamos el atractor y lo eliminamos de $G$ para obtener el juego más pequeño . Nuevamente lo resolvemos por recursión y obtenemos un par de conjuntos ganadores . Se deduce que y . $Estilo de visualización W'_{1-i}}$ ${\estilo de visualización 1-i}$ $Estilo de visualización W'_{1-i}}$ $Estilo de visualización W'_{1-i}}$ $B=Attr_{1-i}(W'_{1-i})$ $G''=G\setmenos B$ $W''_{i},W''_{1-i}$ $W_{i}=W''_{i}$ $W_{1-i}=W''_{1-i}\taza B$

En pseudocódigo simple , el algoritmo podría expresarse así:

función   $p$   := máxima prioridad en  $G$ si retorna de lo contrario  $U$   := nodos en  $G$  con prioridad  $p$ si retorna retorna $resolver(G)$     ${\estilo de visualización p=0}$    $W_{0},W_{1}:=V,\{\}$     $i:=p{\bmod {2}}$   $A:=Attr_{i}(U)$   $W_{0}',W_{1}':=solve(G\setminus A)$    $W_{1-i}'=\{\}$    $W_{i},W_{1-i}:=V,\{\}$   $B:=Attr_{1-i}(W_{1-i}')$   $W_{0}'',W_{1}'':=solve(G\setminus B)$    $W_{i},W_{1-i}:=W_{i}'',W_{1-i}''\cup B$

Juegos relacionados y sus problemas de decisión

Una ligera modificación del juego anterior, y el problema de teoría de grafos relacionado, hace que la resolución del juego sea NP-difícil . El juego modificado tiene la condición de aceptación de Rabin y, por lo tanto, cada vértice está coloreado por un conjunto de colores en lugar de un solo color. En consecuencia, decimos que un vértice v tiene color j si el color j pertenece al conjunto de colores de v . Una jugada infinita es ganadora para el jugador 0 si existe i tal que infinitos vértices en la jugada tienen color 2i , pero un número finito tienen color 2i+1 .

La paridad es el caso especial en el que cada vértice tiene un único color. Específicamente, en el escenario del gráfico bipartito anterior, el problema ahora es determinar si existe una función de elección que seleccione una única arista saliente de cada vértice de V ₀ , de modo que el subgrafo resultante tenga la propiedad de que en cada ciclo (y, por lo tanto, en cada componente fuertemente conectado ) exista un i y un nodo con color 2 i , y ningún nodo con color 2 i + 1...

Tenga en cuenta que, a diferencia de los juegos de paridad, este juego ya no es simétrico con respecto a los jugadores 0 y 1.

Relación con la lógica y la teoría de autómatas

A pesar de su interesante estatus de teoría de la complejidad, la resolución de juegos de paridad puede considerarse como la parte algorítmica de los problemas de verificación automatizada y síntesis de controladores. Por ejemplo, se sabe que el problema de verificación de modelos para el μ-cálculo modal es equivalente a la resolución de juegos de paridad. Asimismo, los problemas de decisión como la validez o la satisfacibilidad de las lógicas modales pueden reducirse a la resolución de juegos de paridad.

Referencias

^ DA Martin : Determinación de Borel, The Annals of Mathematics, vol. 102, n.º 2, págs. 363-371 (1975)
^ Rabin, MO (1969). "Decidibilidad de teorías de segundo orden y autómatas en árboles infinitos". Transactions of the American Mathematical Society . 141 . American Mathematical Society: 1–35. doi :10.2307/1995086. JSTOR 1995086.
^ ab EA Emerson y CS Jutla: Autómatas arbóreos, cálculo mu y determinación, IEEE Proc. Fundamentos de la informática, págs. 368-377 (1991), ISBN 0-8186-2445-0
^ A. Mostowski: Juegos con posiciones prohibidas, Universidad de Gdansk, Informe técnico 78 (1991)
^ Zielonka, W (1998). "Juegos infinitos en gráficos finitamente coloreados con aplicaciones a autómatas en árboles infinitos". Theor. Comput. Sci . 200 (1–2): 135–183. doi : 10.1016/S0304-3975(98)00009-7 .
^ Marcin Jurdziński (1998), "Decidir quién es el ganador en los juegos de paridad está en UP∩ co-UP" (PDF) , Information Processing Letters , 68 (3), Elsevier: 119–124, doi :10.1016/S0020-0190(98)00150-1
^ Calude, Cristian S; Jain, Sanjay; Khoussainov, Bakhadyr; Li, Wei; Stephan, Frank, "Decidir juegos de paridad en tiempo cuasipolinomial" (PDF) , Stoc 2017

Erich Grädel, Phokion G. Kolaitis, Leonid Libkin , Maarten Marx, Joel Spencer , Moshe Y. Vardi , Yde Venema, Scott Weinstein (2007). Teoría de modelos finitos y sus aplicaciones . Springer. ISBN 978-3-540-00428-8.{{cite book}}: CS1 maint: multiple names: authors list (link)

Lectura adicional

E. Grädel, W. Thomas, T. Wilke (Eds.): Autómatas, lógicas y juegos infinitos , Springer LNCS 2500 (2003), ISBN 3-540-00388-6
W. Zielonka: Juegos infinitos en gráficos finitamente coloreados con aplicaciones a autómatas en árboles infinitos , TCS, 200(1-2):135-183, 1998

Enlaces externos

Dos conjuntos de herramientas de resolución de juegos de paridad de última generación son los siguientes:

Colección PGSolver
Gruñir