Un juego de Coronel Blotto es un tipo de juego de suma constante para dos personas en el que los jugadores (oficiales) tienen la tarea de distribuir simultáneamente recursos limitados entre varios objetos (campos de batalla). En la versión clásica del juego, el jugador que dedica más recursos a un campo de batalla gana ese campo de batalla, y la ganancia (o recompensa) es igual al número total de campos de batalla ganados.
El juego fue propuesto por primera vez por Émile Borel [1] en 1921. En 1938, Borel y Ville publicaron una estrategia óptima particular (la solución del "disco"). [2] El juego fue estudiado después de la Segunda Guerra Mundial por académicos en Investigación de Operaciones, y se convirtió en un clásico en la teoría de juegos . [3] El memorando de investigación de Gross y Wagner de 1950 [4] establece la estrategia óptima de Borel y acuñó los nombres ficticios de Coronel Blotto y Enemy. Para tres campos de batalla o más, el espacio de estrategias puras es multidimensional (dos dimensiones para tres campos de batalla) y una estrategia mixta es, por lo tanto, una distribución de probabilidad sobre un conjunto continuo. El juego es un raro ejemplo de un juego no trivial de ese tipo donde se pueden encontrar explícitamente estrategias óptimas.
Además de las aplicaciones de estrategia militar, el juego del Coronel Blotto tiene aplicaciones en la estrategia política (asignación de recursos en campos de batalla políticos), la defensa de redes, las carreras de patentes de I+D y las decisiones de contratación estratégica. Consideremos dos equipos deportivos con topes presupuestarios obligatorios (o dos departamentos de Economía con subvenciones de uso o pérdida) que están buscando el mismo conjunto de candidatos y deben decidir entre muchas ofertas modestas o una búsqueda agresiva de un subconjunto de candidatos.
Como ejemplo de juego de Blotto, considere el juego en el que dos jugadores escriben cada uno tres números enteros positivos en orden no decreciente y de tal manera que sumen un número preestablecido S. Posteriormente, los dos jugadores se muestran mutuamente sus escritos y comparan los números correspondientes. El jugador que tenga dos números mayores que los correspondientes del oponente gana el juego.
Para S = 6 sólo son posibles tres opciones de números: (2, 2, 2), (1, 2, 3) y (1, 1, 4). Es fácil ver que:
De ello se deduce que la estrategia óptima es (2, 2, 2), ya que no es peor que igualar a cualquier otra estrategia y superar a otra estrategia. Sin embargo, existen varios equilibrios de Nash. Si ambos jugadores eligen la estrategia (2, 2, 2) o (1, 2, 3), entonces ninguno de ellos puede superar al otro cambiando de estrategia, por lo que cada par de estrategias es un equilibrio de Nash .
Para valores mayores de S, el juego se vuelve progresivamente más difícil de analizar. Para S = 12, se puede demostrar que (2, 4, 6) representa la estrategia óptima, mientras que para S > 12, las estrategias deterministas no son óptimas. Para S = 13, se puede demostrar que elegir (3, 5, 5), (3, 3, 7) y (1, 5, 7) con una probabilidad de 1/3 cada una es la estrategia probabilística óptima.
El juego de Borel es similar al ejemplo anterior para un valor S muy grande, pero los jugadores no están limitados a números enteros redondos. Por lo tanto, tienen una cantidad infinita de estrategias puras disponibles, de hecho, un continuo.
Este concepto también se implementa en una historia de Sun Bin (田忌赛马) cuando se ve una carrera de carros con tres carreras diferentes que se desarrollan simultáneamente. En las carreras, cada parte tenía la opción de tener un equipo de carros en cada carrera, y cada uno eligió usar una estrategia de 1, 2, 3 (siendo 3 el carro más rápido y 1 el más lento) para desplegar sus carros entre las tres carreras creando victorias ajustadas en cada carrera y pocos resultados seguros para los ganadores. Cuando se le preguntó cómo ganar, Sun Bin aconsejó al dueño del carro que cambiara su despliegue a 2, 3, 1. Aunque estaría seguro de perder la carrera contra los carros más rápidos (los 3 carros); ganaría cada una de las otras carreras, con su carro de 3 superando fácilmente a los carros de 2 y su carro de 2 superando a los carros de 1.
En el caso más simple de dos campos de batalla, Macdonell y Mastronardi 2015 proporcionan la primera caracterización completa de todos los equilibrios de Nash para la versión canónica más simple del juego del Coronel Blotto. Esta solución, que incluye un algoritmo gráfico para caracterizar todas las estrategias de equilibrio de Nash, incluye estrategias de equilibrio de Nash no identificadas previamente y ayuda a identificar qué comportamientos nunca deberían esperarse de los jugadores racionales. Las estrategias de equilibrio de Nash en esta versión del juego son un conjunto de distribuciones de probabilidad bivariadas: distribuciones sobre un conjunto de posibles asignaciones de recursos para cada jugador, a menudo denominadas Equilibrios de Nash Mixtos (como los que se pueden encontrar en Piedra-Papel-Tijera o Monedas a juego como ejemplos mucho más simples).
La solución, prueba y algoritmo gráfico de Macdonell y Mastronardi 2015 para identificar estrategias de equilibrio de Nash también se aplica a versiones generalizadas del juego, como cuando el Coronel Blotto tiene diferentes valoraciones de los campos de batalla, cuando sus recursos tienen diferente efectividad en los dos campos de batalla (por ejemplo, un campo de batalla incluye un desembarco de agua y los recursos del Coronel Blotto son marines en lugar de soldados), y proporciona información sobre versiones del juego con tres o más campos de batalla.
Consideremos dos jugadores (el Coronel Blotto y el Enemigo), dos campos de batalla de igual valor, ambos jugadores conocen el nivel total de recursos del otro antes de la asignación y luego deben tomar una decisión de asignación simultánea. A menudo se supone que el Coronel Blotto es el oficial con más recursos (su nivel de recursos puede definirse como 1) y el Enemigo tiene una fracción de recursos menor que 1. Las estrategias de asignación de equilibrio de Nash y los pagos dependen de esa relación de nivel de recursos.
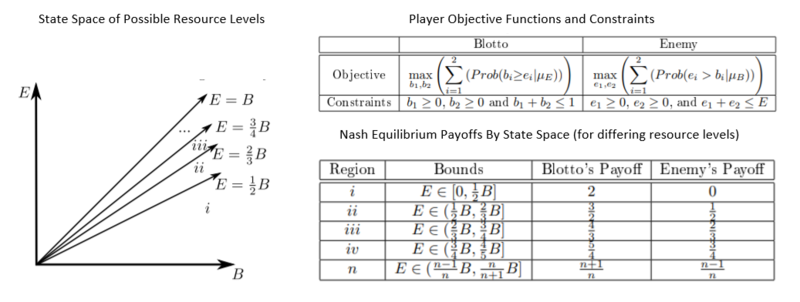
Este juego se utiliza habitualmente como metáfora de la competición electoral, en la que dos partidos políticos dedican dinero o recursos para atraer el apoyo de un número fijo de votantes. [5] [6] Cada votante es un "campo de batalla" que puede ser ganado por uno u otro partido. El mismo juego también encuentra aplicación en la teoría de las subastas, en la que los postores deben realizar ofertas simultáneas. [7]
Jean-François Laslier, [8] Brian Roberson [9] y Dmitriy Kvasov han resuelto varias variaciones del juego original . [10]