suma de riemann

Técnica de aproximación en cálculo integral.

Cuatro de los métodos para aproximar el área bajo curvas. Los métodos izquierdo y derecho realizan la aproximación utilizando los puntos finales derecho e izquierdo de cada subintervalo, respectivamente. Los métodos superior e inferior realizan la aproximación utilizando los valores de punto final más grande y más pequeño de cada subintervalo, respectivamente. Los valores de las sumas convergen cuando los subintervalos se reducen a la mitad desde la parte superior izquierda hasta la parte inferior derecha.

En matemáticas , una suma de Riemann es un cierto tipo de aproximación de una integral por una suma finita. Lleva el nombre del matemático alemán del siglo XIX Bernhard Riemann . Una aplicación muy común es en la integración numérica , es decir, aproximar el área de funciones o rectas en una gráfica, donde también se la conoce como regla del rectángulo . También se puede aplicar para aproximar la longitud de curvas y otras aproximaciones.

La suma se calcula dividiendo la región en formas ( rectángulos , trapecios , parábolas o cúbicas , a veces infinitamente pequeñas) que juntas forman una región similar a la región que se está midiendo, luego se calcula el área para cada una de estas formas y, finalmente, sumando todas estas pequeñas áreas juntas. Este enfoque se puede utilizar para encontrar una aproximación numérica para una integral definida incluso si el teorema fundamental del cálculo no facilita encontrar una solución de forma cerrada .

Debido a que la región de las formas pequeñas generalmente no tiene exactamente la misma forma que la región que se está midiendo, la suma de Riemann será diferente del área que se está midiendo. Este error se puede reducir dividiendo la región más finamente, utilizando formas cada vez más pequeñas. A medida que las formas se hacen cada vez más pequeñas, la suma se acerca a la integral de Riemann .

Definición

Sea una función definida en un intervalo cerrado de los números reales, y como una partición de , es decir, una suma de Riemann de más con partición se define como donde y . ^[1] Se podrían producir diferentes sumas de Riemann dependiendo de cuál se elija. Al final esto no importará, si la función es integrable de Riemann , cuando la diferencia o ancho de los sumandos se acerque a cero. ${\displaystyle f:[a,b]\to \mathbb {R} }$ ${\displaystyle [a,b]}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle P=(x_{0},x_{1},\ldots ,x_{n})}$ ${\displaystyle [a,b]}$ $${\displaystyle a=x_{0}<x_{1}<x_{2}<\dots <x_{n}=b.}$$ ${\displaystyle S}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle P}$ $${\displaystyle S=\sum _{i=1}^{n}f(x_{i}^{*})\,\Delta x_{i},}$$ ${\displaystyle \Delta x_{i}=x_{i}-x_{i-1}}$ ${\displaystyle x_{i}^{*}\in [x_{i-1},x_{i}]}$ ${\displaystyle x_{i}^{*}}$ ${\displaystyle \Delta x_{i}}$

Tipos de sumas de Riemann

Opciones específicas para dar diferentes tipos de sumas de Riemann: ${\displaystyle x_{i}^{*}}$

• Si para todo i , el método es la regla izquierda ^{[2] [3]} y da una suma de Riemann izquierda . ${\displaystyle x_{i}^{*}=x_{i-1}}$
• Si para todo i , el método es la regla correcta ^{[2] [3]} y da una suma de Riemann correcta . ${\displaystyle x_{i}^{*}=x_{i}}$
• Si para todo i , el método es la regla del punto medio ^{[2] [3]} y da una suma de Riemann media . ${\displaystyle x_{i}^{*}=(x_{i}+x_{i-1})/2}$
• Si (es decir, el supremo de over ), el método es la regla superior y da una suma de Riemann superior o una suma de Darboux superior . ${\displaystyle f(x_{i}^{*})=\sup f([x_{i-1},x_{i}])}$ ${\textstyle f}$ ${\displaystyle [x_{i-1},x_{i}]}$
• Si (es decir, el mínimo de f sobre ), el método es la regla inferior y da una suma de Riemann inferior o una suma de Darboux inferior . ${\displaystyle f(x_{i}^{*})=\inf f([x_{i-1},x_{i}])}$ ${\displaystyle [x_{i-1},x_{i}]}$

Todos estos métodos de suma de Riemann se encuentran entre las formas más básicas de lograr la integración numérica . En términos generales, una función es integrable de Riemann si todas las sumas de Riemann convergen a medida que la partición "se vuelve cada vez más fina".

Si bien no se deriva como una suma de Riemann, tomar el promedio de las sumas de Riemann izquierda y derecha es la regla trapezoidal y da una suma trapezoidal . Es una de las formas más simples y muy generales de aproximar integrales utilizando promedios ponderados. A esto le siguen en complejidad la regla de Simpson y las fórmulas de Newton-Cotes .

Cualquier suma de Riemann en una partición determinada (es decir, para cualquier elección entre y ) está contenida entre las sumas de Darboux inferior y superior. Esto forma la base de la integral de Darboux , que en última instancia es equivalente a la integral de Riemann. ${\displaystyle x_{i}^{*}}$ ${\displaystyle x_{i-1}}$ ${\displaystyle x_{i}}$

Métodos de suma de Riemann

Los cuatro métodos de suma de Riemann suelen abordarse mejor con subintervalos de igual tamaño. Por lo tanto, el intervalo [ a , b ] se divide en subintervalos, cada uno de longitud ${\displaystyle n}$ $${\displaystyle \Delta x={\frac {b-a}{n}}.}$$

Los puntos en la partición serán entonces $${\displaystyle a,\;a+\Delta x,\;a+2\Delta x,\;\ldots ,\;a+(n-2)\Delta x,\;a+(n-1)\Delta x,\;b.}$$

gobierno de izquierda

Suma de Riemann izquierda de x ↦ x ³ sobre [0, 2] usando 4 subintervalos

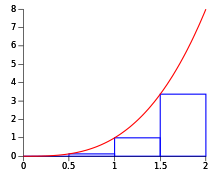
Para la regla de la izquierda, la función se aproxima por sus valores en los extremos izquierdos de los subintervalos. Esto da múltiples rectángulos con base Δ x y altura f ( a + i Δ x ) . Hacer esto para i = 0, 1, ..., n − 1 y sumar las áreas resultantes da $${\displaystyle S_{\mathrm {left} }=\Delta x\left[f(a)+f(a+\Delta x)+f(a+2\Delta x)+\dots +f(b-\Delta x)\right].}$$

La suma de Riemann izquierda equivale a una sobreestimación si f disminuye monótonamente en este intervalo, y a una subestimación si aumenta monótonamente . El error de esta fórmula será dónde está el valor máximo del valor absoluto de durante el intervalo. $${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-S_{\mathrm {left} }\right\vert \leq {\frac {M_{1}(b-a)^{2}}{2n}},}$$ ${\displaystyle M_{1}}$ ${\displaystyle f^{\prime }(x)}$

regla correcta

Suma de Riemann derecha de x ↦ x ³ sobre [0, 2] usando 4 subintervalos

Para la regla correcta, la función se aproxima por sus valores en los extremos derechos de los subintervalos. Esto da múltiples rectángulos con base Δ x y altura f ( a + i Δ x ) . Hacer esto para i = 1, ..., n y sumar las áreas resultantes da $${\displaystyle S_{\mathrm {right} }=\Delta x\left[f(a+\Delta x)+f(a+2\Delta x)+\dots +f(b)\right].}$$

La suma de Riemann correcta equivale a una subestimación si f disminuye monótonamente y a una sobreestimación si aumenta monótonamente . El error de esta fórmula será dónde está el valor máximo del valor absoluto de durante el intervalo. $${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-S_{\mathrm {right} }\right\vert \leq {\frac {M_{1}(b-a)^{2}}{2n}},}$$ ${\displaystyle M_{1}}$ ${\displaystyle f^{\prime }(x)}$

regla del punto medio

Suma de Riemann media de x ↦ x ³ sobre [0, 2] usando 4 subintervalos

Para la regla del punto medio, la función se aproxima por sus valores en los puntos medios de los subintervalos. Esto da f ( a + Δ x /2) para el primer subintervalo, f ( a + 3Δ x /2) para el siguiente, y así sucesivamente hasta f ( b − Δ x /2) . La suma de las áreas resultantes da $${\displaystyle S_{\mathrm {mid} }=\Delta x\left[f\left(a+{\tfrac {\Delta x}{2}}\right)+f\left(a+{\tfrac {3\Delta x}{2}}\right)+\dots +f\left(b-{\tfrac {\Delta x}{2}}\right)\right].}$$

El error de esta fórmula será dónde está el valor máximo del valor absoluto de durante el intervalo. Este error es la mitad del de la suma trapezoidal; como tal, la suma de Riemann media es la aproximación más precisa a la suma de Riemann. $${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-S_{\mathrm {mid} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{24n^{2}}},}$$ ${\displaystyle M_{2}}$ ${\displaystyle f^{\prime \prime }(x)}$

Regla del punto medio generalizada

Una fórmula de regla del punto medio generalizada, también conocida como integración mejorada del punto medio, viene dada por donde denota derivada par. $${\displaystyle \int _{0}^{1}f(x)\,dx=2\sum _{m=1}^{M}{\sum _{n=0}^{\infty }{{\frac {1}{{\left(2M\right)^{2n+1}}\left({2n+1}\right)!}}{{\left.f^{(2n)}(x)\right|}_{x={\frac {m-1/2}{M}}}}}}\,\,,}$$ ${\displaystyle f^{(2n)}}$

Para una función definida en un intervalo , su integral es. Por lo tanto, podemos aplicar esta fórmula de integración del punto medio generalizada asumiendo que . Esta fórmula es particularmente eficiente para la integración numérica cuando el integrando es una función altamente oscilante. ${\displaystyle g(t)}$ ${\displaystyle (a,b)}$ $${\displaystyle \int _{a}^{b}g(t)\,dt=\int _{0}^{b-a}g(\tau +a)\,d\tau =(b-a)\int _{0}^{1}g((b-a)x+a)\,dx.}$$ ${\displaystyle f(x)=(b-a)\,g((b-a)x+a)}$ ${\displaystyle f(x)}$

regla trapezoidal

Suma trapezoidal de x ↦ x ³ sobre [0, 2] usando 4 subintervalos

Para la regla trapezoidal, la función se aproxima por el promedio de sus valores en los extremos izquierdo y derecho de los subintervalos. Usando la fórmula del área para un trapecio con lados paralelos b ₁ y b ₂ y altura h , y sumando las áreas resultantes se obtiene ${\displaystyle {\tfrac {1}{2}}h(b_{1}+b_{2})}$ $${\displaystyle S_{\mathrm {trap} }={\tfrac {1}{2}}\Delta x\left[f(a)+2f(a+\Delta x)+2f(a+2\Delta x)+\dots +f(b)\right].}$$

El error de esta fórmula será donde está el valor máximo del valor absoluto de . $${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-S_{\mathrm {trap} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{12n^{2}}},}$$ ${\displaystyle M_{2}}$ ${\displaystyle f''(x)}$

La aproximación obtenida con la suma trapezoidal de una función es la misma que el promedio de las sumas izquierda y derecha de esa función.

Conexión con la integración

Para una suma de Riemann unidimensional sobre el dominio , a medida que el tamaño máximo de un subintervalo se reduce a cero (es decir, el límite de la norma de los subintervalos llega a cero), algunas funciones harán que todas las sumas de Riemann converjan al mismo valor. Este valor límite, si existe, se define como la integral de Riemann definida de la función sobre el dominio, ${\displaystyle [a,b]}$ $${\displaystyle \int _{a}^{b}f(x)\,dx=\lim _{\|\Delta x\|\rightarrow 0}\sum _{i=1}^{n}f(x_{i}^{*})\,\Delta x_{i}.}$$

Para un dominio de tamaño finito, si el tamaño máximo de un subintervalo se reduce a cero, esto implica que el número de subintervalo llega al infinito. Para particiones finitas, las sumas de Riemann son siempre aproximaciones al valor límite y esta aproximación mejora a medida que la partición se vuelve más fina. Las siguientes animaciones ayudan a demostrar cómo aumentar el número de subintervalos (mientras se reduce el tamaño máximo del subintervalo) se aproxima mejor al "área" bajo la curva:

• 
  Suma de Riemann izquierda
• 
  Suma de Riemann derecha
• 
  Suma de Riemann media

Dado que aquí se supone que la función roja es una función suave , las tres sumas de Riemann convergerán al mismo valor a medida que el número de subintervalos llegue al infinito.

Ejemplo

Comparación de la suma de Riemann derecha con la integral de x ↦ x ² sobre . ${\textstyle [0,2]}$

Tomando un ejemplo, el área bajo la curva y = x ² sobre [0, 2] se puede calcular procedimentalmente utilizando el método de Riemann.

El intervalo [0, 2] se divide en primer lugar en n subintervalos, a cada uno de los cuales se le asigna un ancho de ; estos son los anchos de los rectángulos de Riemann (en adelante "cuadros"). Como se va a utilizar la suma de Riemann correcta, la secuencia de coordenadas x para las cajas será . Por tanto, la secuencia de las alturas de las cajas será . Es un hecho importante que , y . ${\displaystyle {\tfrac {2}{n}}}$ ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ ${\displaystyle x_{1}^{2},x_{2}^{2},\ldots ,x_{n}^{2}}$ ${\displaystyle x_{i}={\tfrac {2i}{n}}}$ ${\displaystyle x_{n}=2}$

El área de cada caja será y por lo tanto la enésima suma de Riemann derecha será: ${\displaystyle {\tfrac {2}{n}}\times x_{i}^{2}}$ $${\displaystyle {\begin{aligned}S&={\frac {2}{n}}\left({\frac {2}{n}}\right)^{2}+\dots +{\frac {2}{n}}\left({\frac {2i}{n}}\right)^{2}+\dots +{\frac {2}{n}}\left({\frac {2n}{n}}\right)^{2}\\[1ex]&={\frac {8}{n^{3}}}\left(1+\dots +i^{2}+\dots +n^{2}\right)\\[1ex]&={\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\right)\\[1ex]&={\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\right)\\[1ex]&={\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}.\end{aligned}}}$$

Si el límite se considera n → ∞, se puede concluir que la aproximación se acerca al valor real del área bajo la curva a medida que aumenta el número de cajas. Por eso: $${\displaystyle \lim _{n\to \infty }S=\lim _{n\to \infty }\left({\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\right)={\frac {8}{3}}.}$$

Este método concuerda con la integral definida calculada de forma más mecánica: $${\displaystyle \int _{0}^{2}x^{2}\,dx={\frac {8}{3}}.}$$

Debido a que la función es continua y monótonamente creciente a lo largo del intervalo, una suma de Riemann por la derecha sobreestima la integral en la mayor cantidad (mientras que una suma de Riemann por la izquierda subestimaría la integral en la mayor cantidad). Este hecho, que resulta intuitivamente claro en los diagramas, muestra cómo la naturaleza de la función determina la precisión con la que se estima la integral. Si bien son simples, las sumas de Riemann derecha e izquierda suelen ser menos precisas que las técnicas más avanzadas para estimar una integral, como la regla trapezoidal o la regla de Simpson .

La función de ejemplo tiene una antiderivada fácil de encontrar, por lo que estimar la integral mediante sumas de Riemann es principalmente un ejercicio académico; sin embargo, hay que recordar que no todas las funciones tienen antiderivadas, por lo que estimar sus integrales mediante sumatoria es prácticamente importante.

Dimensiones superiores

La idea básica detrás de una suma de Riemann es "dividir" el dominio mediante una partición en partes, multiplicar el "tamaño" de cada parte por algún valor que la función toma en esa parte y sumar todos estos productos. Esto se puede generalizar para permitir sumas de Riemann para funciones en dominios de más de una dimensión.

Si bien intuitivamente el proceso de partición del dominio es fácil de comprender, los detalles técnicos de cómo se puede dividir el dominio se vuelven mucho más complicados que el caso unidimensional e involucran aspectos de la forma geométrica del dominio. ^[4]

Dos dimensiones

En dos dimensiones, el dominio se puede dividir en varias celdas bidimensionales tales que . Entonces se puede interpretar que cada celda tiene un "área" indicada por . ^[5] La suma de Riemann bidimensional es donde . ${\displaystyle A}$ ${\displaystyle A_{i}}$ ${\textstyle A=\bigcup _{i}A_{i}}$ ${\displaystyle \Delta A_{i}}$ $${\displaystyle S=\sum _{i=1}^{n}f(x_{i}^{*},y_{i}^{*})\,\Delta A_{i},}$$ ${\displaystyle (x_{i}^{*},y_{i}^{*})\in A_{i}}$

Tres dimensiones

En tres dimensiones, el dominio se divide en varias celdas tridimensionales de modo que . Entonces se puede interpretar que cada celda tiene un "volumen" indicado por . La suma de Riemann tridimensional es ^[6] donde . ${\displaystyle V}$ ${\displaystyle V_{i}}$ ${\textstyle V=\bigcup _{i}V_{i}}$ ${\displaystyle \Delta V_{i}}$ $${\displaystyle S=\sum _{i=1}^{n}f(x_{i}^{*},y_{i}^{*},z_{i}^{*})\,\Delta V_{i},}$$ ${\displaystyle (x_{i}^{*},y_{i}^{*},z_{i}^{*})\in V_{i}}$

Número arbitrario de dimensiones.

Las sumas de Riemann de dimensiones superiores siguen un patrón similar. Una suma de Riemann de n dimensiones es donde , es decir, es un punto en la celda de n dimensiones con volumen de n dimensiones . $${\displaystyle S=\sum _{i}f(P_{i}^{*})\,\Delta V_{i},}$$ ${\displaystyle P_{i}^{*}\in V_{i}}$ ${\displaystyle V_{i}}$ ${\displaystyle \Delta V_{i}}$

Generalización

En general, las sumas de Riemann se pueden escribir donde representa cualquier punto arbitrario contenido en el conjunto y es una medida del conjunto subyacente. En términos generales, una medida es una función que da un "tamaño" de un conjunto, en este caso el tamaño del conjunto ; en una dimensión esto a menudo puede interpretarse como una longitud, en dos dimensiones como un área, en tres dimensiones como un volumen, etc. $${\displaystyle S=\sum _{i}f(P_{i}^{*})\mu (V_{i}),}$$ ${\displaystyle P_{i}^{*}}$ ${\displaystyle V_{i}}$ ${\displaystyle \mu }$ ${\displaystyle V_{i}}$

Ver también

• Antiderivada
• Método de Euler y método del punto medio , métodos relacionados para resolver ecuaciones diferenciales
• Integración de Lebesgue
• Integral de Riemann , límite de sumas de Riemann a medida que la partición se vuelve infinitamente fina
• La regla de Simpson , un poderoso método numérico más poderoso que las sumas básicas de Riemann o incluso la regla trapezoidal
• Regla trapezoidal , método numérico basado en el promedio de la suma de Riemann izquierda y derecha

Referencias

1. Hughes-Hallett, Deborah; McCullum, William G.; et al. (2005). Cálculo (4ª ed.). Wiley. pag. 252.(Entre muchas variaciones equivalentes de la definición, esta referencia se parece mucho a la que se proporciona aquí).
2. Hughes-Hallett, Deborah; McCullum, William G.; et al. (2005). Cálculo (4ª ed.). Wiley. pag. 340. Hasta ahora, tenemos tres formas de estimar una integral usando una suma de Riemann: 1. La regla de la izquierda usa el punto extremo izquierdo de cada subintervalo. 2. La regla correcta utiliza el punto final derecho de cada subintervalo. 3. La regla del punto medio utiliza el punto medio de cada subintervalo.
3. Ostebee, Arnold; Zorn, Paul (2002). Cálculo desde puntos de vista gráficos, numéricos y simbólicos (Segunda ed.). pag. M-33. Las sumas aproximadas de la regla izquierda, la regla derecha y la regla del punto medio se ajustan a esta definición.
4. Swokowski, Earl W. (1979). Cálculo con geometría analítica (Segunda ed.). Boston, MA: Prindle, Weber y Schmidt. págs. 821–822. ISBN 0-87150-268-2.
5. Ostebee, Arnold; Zorn, Paul (2002). Cálculo desde puntos de vista gráficos, numéricos y simbólicos (Segunda ed.). pag. M-34. Cortamos la región plana R en m regiones más pequeñas R ₁ , R ₂ , R ₃ , ..., R _m , quizás de diferentes tamaños y formas. El 'tamaño' de una subregión Ri _ahora se considera su área , denotada por Δ Ai _.
6. Swokowski, Earl W. (1979). Cálculo con geometría analítica (Segunda ed.). Boston, MA: Prindle, Weber y Schmidt. págs. 857–858. ISBN 0-87150-268-2.

enlaces externos

• Weisstein, Eric W. "Suma de Riemann". MundoMatemático .
• Una simulación que muestra la convergencia de sumas de Riemann.