En física , específicamente en mecánica estadística , una inversión de población ocurre cuando un sistema (como un grupo de átomos o moléculas ) existe en un estado en el que más miembros del sistema están en estados de energía más altos y excitados que en estados de energía más bajos y no excitados . Se llama "inversión" porque en muchos sistemas físicos familiares y comunes, esto no es posible. Este concepto es de importancia fundamental en la ciencia del láser porque la producción de una inversión de población es un paso necesario en el funcionamiento de un láser estándar .
Para entender el concepto de inversión de población, es necesario comprender algunos conceptos de termodinámica y la forma en que la luz interactúa con la materia . Para ello, es útil considerar un conjunto muy simple de átomos que forman un medio láser .
Supongamos que hay un grupo de N átomos, cada uno de los cuales es capaz de estar en uno de dos estados de energía :
El número de estos átomos que están en el estado fundamental está dado por N 1 , y el número en el estado excitado N 2 . Como hay N átomos en total,
La diferencia de energía entre los dos estados, dada por
determina la frecuencia característica de la luz que interactuará con los átomos; esto viene dado por la relación
siendo h la constante de Planck .
Si el grupo de átomos está en equilibrio térmico , se puede demostrar a partir de las estadísticas de Maxwell-Boltzmann que la relación del número de átomos en cada estado está dada por la relación de dos distribuciones de Boltzmann , el factor de Boltzmann:
donde T es la temperatura termodinámica del grupo de átomos, k es la constante de Boltzmann y g 1 y g 2 son las degeneraciones de cada estado.
Calculable es la relación de las poblaciones de los dos estados a temperatura ambiente ( T ≈ 300 K ) para una diferencia de energía Δ E que corresponde a la luz de una frecuencia correspondiente a la luz visible ( ν ≈ 5 × 10 14 Hz ). En este caso Δ E = E 2 − E 1 ≈ 2,07 eV, y kT ≈ 0,026 eV. Puesto que E 2 − E 1 ≫ kT , se deduce que el argumento de la exponencial en la ecuación anterior es un número negativo grande, y como tal N 2 / N 1 es extremadamente pequeño; es decir, casi no hay átomos en el estado excitado. Cuando está en equilibrio térmico, entonces, se ve que el estado de menor energía está más poblado que el estado de mayor energía, y este es el estado normal del sistema. A medida que T aumenta, el número de electrones en el estado de alta energía ( N 2 ) aumenta, pero N 2 nunca excede a N 1 para un sistema en equilibrio térmico; más bien, a temperatura infinita, las poblaciones N 2 y N 1 se vuelven iguales. En otras palabras, nunca puede existir una inversión de población ( N 2 / N 1 > 1 ) en un sistema en equilibrio térmico. Por lo tanto, para lograr la inversión de población es necesario llevar el sistema a un estado no equilibrado.
Hay tres tipos de interacciones posibles entre un sistema de átomos y la luz que son de interés:
Si la luz ( fotones ) de frecuencia ν 12 pasa a través del grupo de átomos, existe la posibilidad de que la luz sea absorbida por electrones que se encuentran en el estado fundamental, lo que hará que se exciten al estado de mayor energía. La tasa de absorción es proporcional a la densidad de radiación de la luz y también al número de átomos que se encuentran actualmente en el estado fundamental, N 1 .
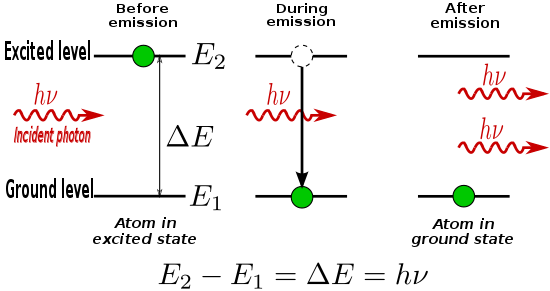
Si los átomos están en estado excitado, se producirán eventos de desintegración espontánea al estado fundamental a una tasa proporcional a N 2 , la cantidad de átomos en el estado excitado. La diferencia de energía entre los dos estados Δ E 21 se emite desde el átomo como un fotón de frecuencia ν 21, como se indica en la relación frecuencia-energía anterior.
Los fotones se emiten de forma estocástica y no existe una relación de fase fija entre los fotones emitidos por un grupo de átomos excitados; en otras palabras, la emisión espontánea es incoherente . En ausencia de otros procesos, el número de átomos en el estado excitado en el momento t está dado por
donde N 2 (0) es el número de átomos excitados en el tiempo t = 0, y τ 21 es la vida media de la transición entre los dos estados.
Si un átomo ya se encuentra en estado excitado, puede ser agitado por el paso de un fotón que tiene una frecuencia ν 21 correspondiente a la brecha de energía Δ E de la transición del estado excitado al estado fundamental. En este caso, el átomo excitado se relaja al estado fundamental y produce un segundo fotón de frecuencia ν 21 . El fotón original no es absorbido por el átomo, por lo que el resultado son dos fotones de la misma frecuencia. Este proceso se conoce como emisión estimulada .
En concreto, un átomo excitado actuará como un pequeño dipolo eléctrico que oscilará con el campo externo proporcionado. Una de las consecuencias de esta oscilación es que fomenta la desintegración de los electrones hasta el estado de menor energía. Cuando esto sucede debido a la presencia del campo electromagnético de un fotón, se libera un fotón en la misma fase y dirección que el fotón "estimulante", y se denomina emisión estimulada.
La velocidad a la que se produce la emisión estimulada es proporcional al número de átomos N 2 en el estado excitado y a la densidad de radiación de la luz. Albert Einstein demostró que la probabilidad base de que un fotón provoque una emisión estimulada en un solo átomo excitado es exactamente igual a la probabilidad de que un fotón sea absorbido por un átomo en el estado fundamental. Por lo tanto, cuando el número de átomos en los estados fundamental y excitado es igual, la velocidad de emisión estimulada es igual a la velocidad de absorción para una densidad de radiación dada.
El detalle crítico de la emisión estimulada es que el fotón inducido tiene la misma frecuencia y fase que el fotón incidente. En otras palabras, los dos fotones son coherentes . Es esta propiedad la que permite la amplificación óptica y la producción de un sistema láser . Durante el funcionamiento de un láser, tienen lugar las tres interacciones luz-materia descritas anteriormente. Inicialmente, los átomos se energizan desde el estado fundamental al estado excitado mediante un proceso llamado bombeo , que se describe a continuación. Algunos de estos átomos se desintegran mediante emisión espontánea, liberando luz incoherente como fotones de frecuencia ν . Estos fotones se devuelven al medio láser, normalmente mediante un resonador óptico . Algunos de estos fotones son absorbidos por los átomos en el estado fundamental y se pierden en el proceso láser. Sin embargo, algunos fotones provocan una emisión estimulada en átomos en estado excitado, liberando otro fotón coherente. En efecto, esto da como resultado la amplificación óptica .
Si el número de fotones que se amplifican por unidad de tiempo es mayor que el número de fotones que se absorben, entonces el resultado neto es un número continuamente creciente de fotones producidos; se dice que el medio láser tiene una ganancia mayor que la unidad.
Recordemos de las descripciones de absorción y emisión estimulada anteriores que las tasas de estos dos procesos son proporcionales al número de átomos en los estados fundamental y excitado, N 1 y N 2 , respectivamente. Si el estado fundamental tiene una población mayor que el estado excitado ( N 1 > N 2 ), entonces el proceso de absorción domina, y hay una atenuación neta de fotones. Si las poblaciones de los dos estados son las mismas ( N 1 = N 2 ), la tasa de absorción de luz equilibra exactamente la tasa de emisión; entonces se dice que el medio es ópticamente transparente .
Si el estado de mayor energía tiene una población mayor que el estado de menor energía ( N 1 < N 2 ), entonces el proceso de emisión domina y la luz en el sistema experimenta un aumento neto en intensidad. Por lo tanto, es claro que para producir una tasa más rápida de emisiones estimuladas que de absorciones, se requiere que la relación de las poblaciones de los dos estados sea tal que N 2 / N 1 > 1; En otras palabras, se requiere una inversión de población para el funcionamiento del láser.
Muchas transiciones que involucran radiación electromagnética están estrictamente prohibidas bajo la mecánica cuántica. Las transiciones permitidas se describen mediante las llamadas reglas de selección , que describen las condiciones bajo las cuales se permite una transición radiativa. Por ejemplo, las transiciones solo se permiten si Δ S = 0, siendo S el momento angular de espín total del sistema. En materiales reales, otros efectos, como las interacciones con la red cristalina, intervienen para eludir las reglas formales proporcionando mecanismos alternativos. En estos sistemas, las transiciones prohibidas pueden ocurrir, pero generalmente a velocidades más lentas que las transiciones permitidas. Un ejemplo clásico es la fosforescencia , donde un material tiene un estado fundamental con S = 0, un estado excitado con S = 0 y un estado intermedio con S = 1. La transición del estado intermedio al estado fundamental por emisión de luz es lenta debido a las reglas de selección. Por lo tanto, la emisión puede continuar después de que se elimine la iluminación externa. En contraste, la fluorescencia en los materiales se caracteriza por una emisión que cesa cuando se elimina la iluminación externa.
Las transiciones que no implican la absorción o emisión de radiación no se ven afectadas por las reglas de selección. La transición sin radiación entre niveles, como entre los estados excitados S = 0 y S = 1, puede ocurrir con la suficiente rapidez como para absorber una parte de la población S = 0 antes de que regrese espontáneamente al estado fundamental.
La existencia de estados intermedios en los materiales es esencial para la técnica de bombeo óptico de láseres (ver más abajo).
Para que el láser funcione es necesaria una inversión de población , pero no se puede lograr en el grupo teórico de átomos con dos niveles de energía mencionado anteriormente cuando están en equilibrio térmico. De hecho, cualquier método por el cual los átomos se exciten de manera directa y continua desde el estado fundamental al estado excitado (como la absorción óptica) alcanzará finalmente el equilibrio con los procesos de desexcitación de emisión espontánea y estimulada. En el mejor de los casos, se puede lograr una población igual de los dos estados, N 1 = N 2 = N /2, lo que da como resultado transparencia óptica pero no ganancia óptica neta.
Para lograr condiciones de no equilibrio duraderas, se debe utilizar un método indirecto para poblar el estado excitado. Para entender cómo se hace esto, considere un modelo ligeramente más realista, el de un láser de tres niveles . Considere nuevamente un grupo de N átomos, esta vez con cada átomo capaz de existir en cualquiera de los tres estados de energía, niveles 1, 2 y 3, con energías E 1 , E 2 y E 3 , y poblaciones N 1 , N 2 y N 3 , respectivamente.
Supongamos que E 1 < E 2 < E 3 ; es decir, la energía del nivel 2 se encuentra entre la del estado fundamental y la del nivel 3.
Inicialmente, el sistema de átomos está en equilibrio térmico, y la mayoría de los átomos estarán en el estado fundamental, es decir, N 1 ≈ N , N 2 ≈ N 3 ≈ 0 . Si los átomos se someten a luz de una frecuencia , el proceso de absorción óptica excitará los electrones desde el estado fundamental al nivel 3. Este proceso se llama bombeo , y no necesariamente implica siempre directamente la absorción de luz; se pueden utilizar otros métodos de excitación del medio láser, como la descarga eléctrica o las reacciones químicas. El nivel 3 a veces se denomina nivel de bombeo o banda de bombeo , y la transición de energía E 1 → E 3 como la transición de bombeo , que se muestra como la flecha marcada P en el diagrama de la derecha.
Al bombear el medio, un número apreciable de átomos pasará al nivel 3, de modo que N 3 > 0 . Para tener un medio adecuado para el funcionamiento del láser, es necesario que estos átomos excitados decaigan rápidamente al nivel 2. La energía liberada en esta transición puede emitirse como un fotón (emisión espontánea), sin embargo, en la práctica, la transición 3 → 2 llamada efecto Auger (etiquetada como R en el diagrama) suele ser sin radiación , y la energía se transfiere al movimiento vibratorio ( calor ) del material anfitrión que rodea a los átomos, sin la generación de un fotón.
Un electrón en el nivel 2 puede decaer por emisión espontánea al estado fundamental, liberando un fotón de frecuencia ν 12 (dada por E 2 − E 1 = hν 12 ), que se muestra como la transición L , llamada transición láser en el diagrama. Si el tiempo de vida de esta transición, τ 21 es mucho más largo que el tiempo de vida de la transición sin radiación 3 → 2 τ 32 (si τ 21 ≫ τ 32 , conocido como una razón de tiempo de vida favorable ), la población de E 3 será esencialmente cero ( N 3 ≈ 0 ) y una población de átomos en estado excitado se acumulará en el nivel 2 ( N 2 > 0 ). Si más de la mitad de los N átomos se pueden acumular en este estado, esto superará la población del estado fundamental N 1 . De esta forma se ha conseguido una inversión de población ( N 2 > N 1 ) entre el nivel 1 y 2, y se puede obtener una amplificación óptica en la frecuencia ν 21 .
Debido a que al menos la mitad de la población de átomos debe ser excitada desde el estado fundamental para obtener una inversión de población, el medio láser debe ser bombeado muy fuertemente. Esto hace que los láseres de tres niveles sean bastante ineficientes, a pesar de ser el primer tipo de láser que se descubrió (basado en un medio láser de rubí , por Theodore Maiman en 1960). Un sistema de tres niveles también podría tener una transición radiativa entre el nivel 3 y 2, y una transición no radiativa entre 2 y 1. En este caso, los requisitos de bombeo son más débiles. En la práctica, la mayoría de los láseres son láseres de cuatro niveles , descritos a continuación.
Aquí hay cuatro niveles de energía, energías E 1 , E 2 , E 3 , E 4 y poblaciones N 1 , N 2 , N 3 , N 4 , respectivamente. Las energías de cada nivel son tales que E 1 < E 2 < E 3 < E 4 .
En este sistema, la transición de bombeo P excita los átomos en el estado fundamental (nivel 1) hacia la banda de bombeo (nivel 4). Desde el nivel 4, los átomos se desintegran nuevamente mediante una transición rápida y no radiactiva Ra hacia el nivel 3. Dado que la vida útil de la transición láser L es larga en comparación con la de Ra ( τ 32 ≫ τ 43 ), se acumula una población en el nivel 3 (el nivel láser superior ), que puede relajarse por emisión espontánea o estimulada hacia el nivel 2 (el nivel láser inferior ). Este nivel también tiene una desintegración rápida y no radiactiva Rb hacia el estado fundamental.
Como antes, la presencia de una transición de desintegración rápida y sin radiación da como resultado que la población de la banda de bombeo se agote rápidamente ( N 4 ≈ 0). En un sistema de cuatro niveles, cualquier átomo en el nivel láser inferior E 2 también se desexcita rápidamente, lo que lleva a una población insignificante en ese estado ( N 2 ≈ 0). Esto es importante, ya que cualquier población apreciable que se acumule en el nivel 3, el nivel láser superior, formará una inversión de población con respecto al nivel 2. Es decir, mientras N 3 > 0, entonces N 3 > N 2 , y se logra una inversión de población. Por lo tanto, la amplificación óptica y el funcionamiento del láser pueden tener lugar a una frecuencia de ν 32 ( E 3 − E 2 = hν 32 ).
Dado que sólo se deben excitar unos pocos átomos en el nivel láser superior para formar una inversión de población, un láser de cuatro niveles es mucho más eficiente que uno de tres niveles, y la mayoría de los láseres prácticos son de este tipo. En realidad, en el proceso láser pueden estar involucrados muchos más de cuatro niveles de energía, con complejos procesos de excitación y relajación involucrados entre estos niveles. En particular, la banda de bombeo puede constar de varios niveles de energía distintos, o un continuo de niveles, que permiten el bombeo óptico del medio en un amplio rango de longitudes de onda.
Tenga en cuenta que, tanto en los láseres de tres como de cuatro niveles, la energía de la transición de bombeo es mayor que la de la transición láser. Esto significa que, si el láser se bombea ópticamente, la frecuencia de la luz de bombeo debe ser mayor que la de la luz láser resultante. En otras palabras, la longitud de onda de bombeo es más corta que la longitud de onda láser. En algunos medios, es posible utilizar múltiples absorciones de fotones entre múltiples transiciones de menor energía para alcanzar el nivel de bombeo; dichos láseres se denominan láseres de conversión ascendente .
Si bien en muchos láseres el proceso láser implica la transición de átomos entre diferentes estados de energía electrónica , como se describe en el modelo anterior, este no es el único mecanismo que puede dar lugar a la acción del láser. Por ejemplo, hay muchos láseres comunes (por ejemplo, láseres de colorante , láseres de dióxido de carbono ) en los que el medio láser consta de moléculas completas y los estados de energía corresponden a modos de oscilación vibracional y rotacional de las moléculas. Este es el caso de los máseres de agua , que se producen en la naturaleza .
En algunos medios es posible, imponiendo un campo óptico o de microondas adicional, utilizar efectos de coherencia cuántica para reducir la probabilidad de una transición del estado fundamental al estado excitado. Esta técnica, conocida como láser sin inversión , permite que se produzca una amplificación óptica sin producir una inversión de población entre los dos estados.
La emisión estimulada se observó por primera vez en la región de microondas del espectro electromagnético, lo que dio origen al acrónimo MASER ( Microondas Amplificación por Emisión Estimulada de Radiación). En la región de microondas, la distribución de Boltzmann de las moléculas entre los estados de energía es tal que, a temperatura ambiente, todos los estados están poblados casi por igual.
Para crear una inversión de población en estas condiciones, es necesario eliminar selectivamente algunos átomos o moléculas del sistema en función de las diferencias en las propiedades. Por ejemplo, en un máser de hidrógeno , la conocida transición de onda de 21 cm en el hidrógeno atómico , donde el electrón solitario cambia su estado de espín de paralelo al espín nuclear a antiparalelo, se puede utilizar para crear una inversión de población porque el estado paralelo tiene un momento magnético y el estado antiparalelo no. Un campo magnético no homogéneo fuerte separará los átomos en el estado de mayor energía de un haz de átomos de estado mixto. La población separada representa una inversión de población que puede exhibir emisiones estimuladas.