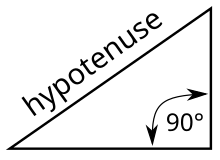
En geometría , una hipotenusa es el lado de un triángulo rectángulo opuesto al ángulo recto . [1] Es el lado más largo de cualquier triángulo de este tipo; los otros dos lados más cortos de dicho triángulo se llaman catetos . La longitud de la hipotenusa se puede encontrar utilizando el teorema de Pitágoras , que establece que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los dos catetos. Matemáticamente, esto se puede escribir como , donde a es la longitud de un cateto, b es la longitud del otro cateto y c es la longitud de la hipotenusa. [2]
Por ejemplo, si uno de los catetos de un ángulo recto tiene una longitud de 3 y el otro tiene una longitud de 4, entonces sus cuadrados suman 25 = 9 + 16 = 3 × 3 + 4 × 4. Como 25 es el cuadrado de la hipotenusa, la longitud de la hipotenusa es la raíz cuadrada de 25, es decir, 5. En otras palabras, si y , entonces .
La palabra hipotenusa se deriva del griego ἡ τὴν ὀρθὴν γωνίαν ὑποτείνουσα (sc. γραμμή o πλευρά ), que significa "[lado] que subtiende el ángulo recto" ( Apolodoro ), [3] ὑ ποτείνουσα hupoteinousa siendo el participio presente activo femenino del verbo ὑποτείνω hupo -teinō "estirar debajo, subtender", de τείνω teinō "estirar, extender". El participio nominalizado, ἡ ὑποτείνουσα , se utilizó para la hipotenusa de un triángulo en el siglo IV a. C. (atestiguado en Platón , Timeo 54d). El término griego fue prestado al latín tardío , como hypotēnūsa . [4] [5] La ortografía en -e , como hipotenusa , es de origen francés ( Estienne de La Roche 1520). [6]

En un triángulo rectángulo , la hipotenusa es el lado opuesto al ángulo recto , mientras que los otros dos lados se denominan catetos o catetos . [7] La longitud de la hipotenusa se puede calcular utilizando la función raíz cuadrada implícita en el teorema de Pitágoras . Afirma que la suma de los dos catetos al cuadrado es igual a la hipotenusa al cuadrado. En notación matemática, con los respectivos catetos etiquetados como a y b , y la hipotenusa etiquetada como c , se escribe como . Usando la función raíz cuadrada en ambos lados de la ecuación, se deduce que
Como consecuencia del teorema de Pitágoras, la hipotenusa es el lado más largo de cualquier triángulo rectángulo; es decir, la hipotenusa es más larga que cualquiera de los catetos del triángulo. Por ejemplo, dada la longitud de los catetos a = 5 y b = 12, entonces la suma de los catetos al cuadrado es (5 × 5) + (12 × 12) = 169, el cuadrado de la hipotenusa. La longitud de la hipotenusa es, por lo tanto, la raíz cuadrada de 169, denotada , que es igual a 13.
El teorema de Pitágoras, y por lo tanto esta longitud, también se puede derivar de la ley de los cosenos en trigonometría . En un triángulo rectángulo, el coseno de un ángulo es la razón entre el cateto adyacente al ángulo y la hipotenusa. Para un ángulo recto γ (gamma), donde el cateto adyacente es igual a 0, el coseno de γ también es igual a 0. La ley de los cosenos formula que se cumple para algún ángulo θ (theta). Observando que el ángulo opuesto a la hipotenusa es recto y notando que su coseno es 0, entonces en este caso θ = γ = 90°:
Muchos lenguajes de computadora admiten la función estándar ISO C hypot( x , y ), que devuelve el valor anterior. [8] La función está diseñada para no fallar donde el cálculo directo podría desbordarse o desbordarse por debajo de su capacidad y puede ser ligeramente más precisa y, a veces, significativamente más lenta.
Algunos lenguajes han extendido la definición a dimensiones superiores. Por ejemplo, C++17 admite ; [9] esto da la longitud de la diagonal de un cuboide rectangular con aristas x , y y z . Python 3.8 se amplió para manejar una cantidad arbitraria de argumentos. [10]
Algunas calculadoras científicas [ ¿cuáles? ] proporcionan una función para convertir coordenadas rectangulares a coordenadas polares . Esto proporciona tanto la longitud de la hipotenusa como el ángulo que forma la hipotenusa con la línea base ( c 1 arriba) al mismo tiempo cuando se dan x e y . El ángulo devuelto normalmente se da por atan2 ( y , x ).
Mediante razones trigonométricas se puede obtener el valor de dos ángulos agudos, y , del triángulo rectángulo.
Dada la longitud de la hipotenusa y de un cateto , la relación es:

La función inversa trigonométrica es:
en el cual se encuentra el ángulo opuesto al cateto .
El ángulo adyacente del catetos es = 90° –
También se puede obtener el valor del ángulo mediante la ecuación:
en el cual está el otro cateto.
...Además, un triángulo rectángulo tiene un ángulo recto, y el lado opuesto a este ángulo se llama hipotenusa;...