Método de expansiones asintóticas emparejadas.

En matemáticas , el método de expansiones asintóticas emparejadas ^[1] es un enfoque común para encontrar una aproximación precisa a la solución de una ecuación o sistema de ecuaciones . Se utiliza particularmente al resolver ecuaciones diferenciales singularmente perturbadas . Implica encontrar varias soluciones aproximadas diferentes, cada una de las cuales es válida (es decir, precisa) para parte del rango de la variable independiente, y luego combinar estas diferentes soluciones para dar una única solución aproximada que sea válida para todo el rango de valores de la variable independiente. En la literatura rusa, estos métodos se conocían con el nombre de "asintóticas intermedias" y fueron introducidos en los trabajos de Yakov Zeldovich y Grigory Barenblatt .

Descripción general del método

En una gran clase de problemas singularmente perturbados, el dominio puede dividirse en dos o más subdominios. En uno de ellos, a menudo el más grande, la solución se aproxima con precisión mediante una serie asintótica ^[2] que se encuentra tratando el problema como una perturbación regular (es decir, estableciendo un parámetro relativamente pequeño en cero). Los otros subdominios consisten en una o más regiones pequeñas en las que esa aproximación es inexacta, generalmente porque los términos de perturbación en el problema no son despreciables allí. Estas áreas se denominan capas de transición en general, y específicamente como capas límite o capas interiores dependiendo de si ocurren en el límite del dominio (como es el caso habitual en las aplicaciones) o dentro del dominio, respectivamente.

Se obtiene una aproximación en forma de serie asintótica en la(s) capa(s) de transición tratando esa parte del dominio como un problema de perturbación separado. Esta aproximación se llama solución interna y la otra es solución externa , llamada así por su relación con las capas de transición. Luego, las soluciones externa e interna se combinan mediante un proceso llamado "emparejamiento" de tal manera que se obtiene una solución aproximada para todo el dominio. ^{[3] [4] [5] [6]}

Un ejemplo sencillo

Considere el problema del valor límite

$${\displaystyle \varepsilon y''+(1+\varepsilon )y'+y=0,}$$

${\displaystyle y}$ ${\displaystyle t}$ ${\displaystyle y(0)=0}$ ${\displaystyle y(1)=1}$ ${\displaystyle \varepsilon }$ ${\displaystyle 0<\varepsilon \ll 1}$

Solución exterior, válida para t  =  O (1)

Dado que es muy pequeña, nuestro primer enfoque es tratar la ecuación como un problema de perturbación regular, es decir, hacer la aproximación y, por tanto, encontrar la solución al problema. ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon =0}$

$${\displaystyle y'+y=0.}$$

Alternativamente, considere que cuando y son ambos de tamaño O (1), los cuatro términos en el lado izquierdo de la ecuación original son respectivamente de tamaños , O (1) y O (1). El saldo de orden líder en esta escala de tiempo, válido en el límite distinguido , viene dado por los términos segundo y cuarto, es decir, ${\displaystyle y}$ ${\displaystyle t}$ ${\displaystyle O(\varepsilon )}$ ${\displaystyle O(\varepsilon )}$ ${\displaystyle \varepsilon \to 0}$ ${\displaystyle y'+y=0.}$

esto tiene solucion

$${\displaystyle y=Ae^{-t}}$$

de perturbación singular ${\displaystyle A}$ ${\displaystyle y(0)=0}$ ${\displaystyle A=0}$ ${\displaystyle y(1)=1}$ ${\displaystyle A=e}$ ${\displaystyle \varepsilon =0}$ ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle \varepsilon }$ ${\displaystyle t=0}$ ${\displaystyle y(1)=1}$ ${\displaystyle A=e}$ ${\displaystyle y_{\mathrm {O} }=e^{1-t}}$

Solución interna, válida para t  =  O ( ε )

En la región interior, y son ambos pequeños, pero de tamaño comparable, por lo que se define la nueva variable de tiempo O (1) . Vuelva a escalar el problema de valor límite original reemplazándolo con y el problema se convierte en ${\displaystyle t}$ ${\displaystyle \varepsilon }$ ${\displaystyle \tau =t/\varepsilon }$ ${\displaystyle t}$ ${\displaystyle \tau \varepsilon }$

$${\displaystyle {\frac {1}{\varepsilon }}y''(\tau )+\left({1+\varepsilon }\right){\frac {1}{\varepsilon }}y'(\tau )+y(\tau )=0,}$$

${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon =0}$

$${\displaystyle y''+y'=0.}$$

Alternativamente, considere que cuando se ha reducido al tamaño , entonces todavía es de tamaño O (1) (usando la expresión para ), por lo que los cuatro términos en el lado izquierdo de la ecuación original son respectivamente de tamaños , , O (1) y O (1). El saldo de orden líder en esta escala de tiempo, válido en el límite distinguido , viene dado por tanto por el primer y segundo términos, es decir ${\displaystyle t}$ ${\displaystyle O(\varepsilon )}$ ${\displaystyle y}$ ${\displaystyle y_{\mathrm {O} }}$ ${\displaystyle O(\varepsilon ^{-1})}$ ${\displaystyle O(\varepsilon ^{-1})}$ ${\displaystyle \varepsilon \to 0}$ ${\displaystyle y''+y'=0.}$

esto tiene solucion

$${\displaystyle y=B-Ce^{-\tau }}$$

${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle y(0)=0}$ ${\displaystyle B=C}$

$${\displaystyle y_{\mathrm {I} }=B\left({1-e^{-\tau }}\right)=B\left({1-e^{-t/\varepsilon }}\right).}$$

Pareo

Usamos el emparejamiento para encontrar el valor de la constante . La idea de hacer coincidir es que las soluciones interna y externa deben coincidir para los valores de en una región intermedia (o superpuesta), es decir, donde . Necesitamos que el límite exterior de la solución interior coincida con el límite interior de la solución exterior, es decir, ${\displaystyle B}$ ${\displaystyle t}$ ${\displaystyle \varepsilon \ll t\ll 1}$

$${\displaystyle \lim _{\tau \to \infty }y_{\mathrm {I} }=\lim _{t\to 0}y_{\mathrm {O} },}$$

${\displaystyle B=e}$

El problema anterior es el más simple de los problemas simples que tratan con expansiones asintóticas emparejadas. Se puede calcular inmediatamente que es toda la serie asintótica para la región exterior, mientras que la corrección a la solución interior es y la constante de integración debe obtenerse del emparejamiento interior-exterior. ${\displaystyle e^{1-t}}$ ${\displaystyle {\mathcal {O}}(\varepsilon )}$ ${\displaystyle y_{\mathrm {I} }}$ ${\textstyle B(1-e^{-t/\varepsilon })}$ ${\displaystyle B}$

Observe que la idea intuitiva de hacer coincidir los límites, es decir, no se aplica a este nivel. Esto se debe simplemente a que el término subrayado no converge a un límite. Los métodos a seguir en este tipo de casos son optar por a) el método de una variable intermedia o utilizar b) la regla de coincidencia de Van-Dyke. El primer método es engorroso y siempre funciona, mientras que la regla de coincidencia de Van-Dyke es fácil de implementar pero con aplicabilidad limitada. Un problema concreto de valores límite que tiene todos los ingredientes esenciales es el siguiente. ${\textstyle \lim _{\tau \to \infty }y_{\mathrm {I} }=\lim _{t\to 0}y_{\mathrm {O} },}$

Considere el problema del valor límite

$${\displaystyle \varepsilon y''-x^{2}y'-y=1,\quad y(0)=y(1)=1}$$

La expansión exterior convencional da , donde se debe obtener haciendo coincidir. ${\displaystyle y_{\mathrm {O} }=y_{0}+\varepsilon y_{1}+\cdots }$ ${\displaystyle y_{0}=\alpha e^{1/x}-1}$ ${\displaystyle \alpha }$

El problema tiene capas límite tanto a la izquierda como a la derecha. La capa límite izquierda cerca tiene un espesor mientras que la capa límite derecha cerca tiene espesor . Primero calculemos la solución en la capa límite izquierda reescalando , luego la ecuación diferencial a satisfacer en la izquierda es ${\displaystyle 0}$ ${\displaystyle \varepsilon ^{1/2}}$ ${\displaystyle 1}$ ${\displaystyle \varepsilon }$ ${\displaystyle X=x/\varepsilon ^{1/2},\;Y=y}$

$${\displaystyle Y''-\varepsilon ^{1/2}X^{2}Y'-Y=1,\quad Y(0)=1}$$

${\displaystyle Y^{l}=Y_{0}^{l}+\varepsilon ^{1/2}Y_{1/2}^{l}+\cdots }$

La condición no homogénea de la izquierda nos proporciona la razón para iniciar la expansión en . La solución de orden líder es . ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle Y_{0}^{l}=2e^{-X}-1}$

Esto con la combinación de Van-Dyke da . ${\displaystyle 1-1}$ ${\displaystyle \alpha =0}$

Calculemos ahora la solución del reescalamiento de la derecha , luego la ecuación diferencial a satisfacer a la derecha es ${\displaystyle X=(1-x)/\varepsilon ,\;Y=y}$

$${\displaystyle Y''+\left(1-2\varepsilon X+\varepsilon ^{2}X^{2}\right)Y'-\varepsilon Y=\varepsilon ,\quad Y(1)=1,}$$

$${\displaystyle Y^{r}=Y_{0}^{r}+\varepsilon Y_{1}^{r}+\cdots .}$$

La condición no homogénea de la derecha nos proporciona la razón para comenzar la expansión en . La solución de orden líder es . Esto con la combinación de Van-Dyke da . Procediendo de manera similar, si calculamos las correcciones de orden superior, obtenemos las soluciones como ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle Y_{0}^{r}=(1-B)+Be^{-X}}$ ${\displaystyle 1-1}$ ${\displaystyle B=2}$

$${\displaystyle Y^{l}=2e^{-X}-1+\varepsilon ^{1/2}e^{-X}\left({\frac {X^{3}}{3}}+{\frac {X^{2}}{2}}+{\frac {X}{2}}\right)+{\mathcal {O}}(\varepsilon ),\quad X={\frac {x}{\varepsilon ^{1/2}}}.}$$

$${\displaystyle y\equiv -1.}$$

$${\displaystyle Y^{r}=2e^{-X}-1+2\varepsilon e^{-X}\left(X+X^{2}\right)+{\mathcal {O}}(\varepsilon ^{2}),\quad X={\frac {1-x}{\varepsilon }}.}$$

solución compuesta

Para obtener nuestra solución compuesta final, emparejada y válida en todo el dominio, un método popular es el método uniforme. En este método, sumamos las aproximaciones interna y externa y restamos su valor superpuesto, que de otro modo se contaría dos veces. El valor de superposición es el límite exterior de la solución de la capa límite interna y el límite interno de la solución externa; Se encontró que estos límites eran iguales . Por lo tanto, la solución final aproximada a este problema de valores en la frontera es, ${\displaystyle \,y_{\mathrm {overlap} }}$ ${\displaystyle e}$

$${\displaystyle y(t)=y_{\mathrm {I} }+y_{\mathrm {O} }-y_{\mathrm {overlap} }=e\left({1-e^{-t/\varepsilon }}\right)+e^{1-t}-e=e\left({e^{-t}-e^{-t/\varepsilon }}\right).}$$

Tenga en cuenta que esta expresión se reduce correctamente a las expresiones para y cuando es y O (1), respectivamente. ${\displaystyle y_{\mathrm {I} }}$ ${\displaystyle y_{\mathrm {O} }}$ ${\displaystyle t}$ ${\displaystyle O(\varepsilon )}$

Exactitud

Convergencia de aproximaciones. Se muestran aproximaciones y soluciones exactas, que son indistinguibles a esta escala, para varios . También se muestra la solución exterior. Tenga en cuenta que dado que la capa límite se vuelve más estrecha al disminuir , las aproximaciones convergen a la solución exterior puntualmente , pero no de manera uniforme , en casi todas partes. ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$

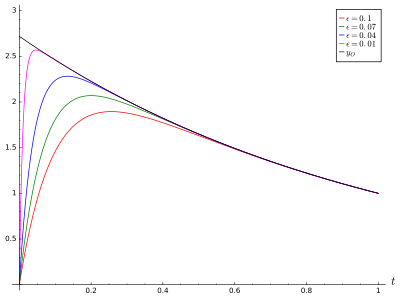
Esta solución final satisface la ecuación diferencial original del problema (que se muestra al sustituirla y sus derivadas en la ecuación original). Además, las condiciones de contorno producidas por esta solución final coinciden con los valores dados en el problema, hasta un múltiplo constante. Esto implica, debido a la unicidad de la solución, que la solución asintótica emparejada es idéntica a la solución exacta hasta un múltiplo constante. Este no es necesariamente siempre el caso; los términos restantes deben llegar a cero de manera uniforme como . ${\displaystyle \varepsilon \rightarrow 0}$

Nuestra solución no sólo resuelve con éxito aproximadamente el problema en cuestión, sino que se aproxima mucho a la solución exacta del problema. Sucede que es fácil encontrar que este problema en particular tiene una solución exacta.

$${\displaystyle y(t)={\frac {e^{-t}-e^{-t/\varepsilon }}{e^{-1}-e^{-1/\varepsilon }}},}$$

${\displaystyle e^{1-1/\varepsilon }}$

Ubicación de la capa límite

Convenientemente, podemos ver que la capa límite, donde y son grandes, está cerca de , como supusimos anteriormente. Si hubiéramos supuesto que estaba en el otro punto final y procediéramos a realizar el cambio de escala , nos habría resultado imposible satisfacer la condición de coincidencia resultante. Para muchos problemas, este tipo de prueba y error es la única forma de determinar la verdadera ubicación de la capa límite. ^[3] ${\displaystyle y'}$ ${\displaystyle y''}$ ${\displaystyle t=0}$ ${\displaystyle \tau =(1-t)/\varepsilon }$

Problemas más difíciles

El problema anterior es un ejemplo simple porque es una ecuación única con una sola variable dependiente y hay una capa límite en la solución. Los problemas más difíciles pueden contener varias variables codependientes en un sistema de varias ecuaciones y/o con varias capas límite y/o interiores en la solución.

A menudo es deseable encontrar más términos en las expansiones asintóticas de las soluciones tanto externas como internas. La forma apropiada de estas expansiones no siempre está clara: si bien una expansión en serie de potencias puede funcionar, a veces la forma apropiada involucra potencias fraccionarias de , funciones como , etcétera. Como en el ejemplo anterior, obtendremos expansiones externas e internas con algunos coeficientes que deben determinarse mediante coincidencia. ^[7] ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon \log \varepsilon }$

Ecuaciones diferenciales de segundo orden

Ecuaciones diferenciales de segundo orden tipo Schrödinger

Dingle y Müller-Kirsten han desarrollado y utilizado ampliamente un método de expansiones asintóticas emparejadas (con emparejamiento de soluciones en el dominio común de validez) para derivar expansiones asintóticas de las soluciones y números característicos (límites de banda) de sistemas tipo Schrödinger. ecuaciones diferenciales de segundo orden con potenciales periódicos, en particular para la ecuación de Mathieu ^[8] (mejor ejemplo), ecuaciones de ondas elipsoidales y de Lamé, ^[9] ecuaciones de ondas esferoidales achatadas ^[10] y prolatas ^[11] , y ecuaciones con potenciales anarmónicos . ^[12]

Ecuaciones de convección-difusión

Se han desarrollado métodos de expansiones asintóticas emparejadas para encontrar soluciones aproximadas a la ecuación de convección-difusión de Smoluchowski , que es una ecuación diferencial de segundo orden singularmente perturbada. El problema se ha estudiado particularmente en el contexto de partículas coloides en campos de flujo lineal, donde la variable viene dada por la función de distribución de pares alrededor de una partícula de prueba. En el límite del número de Péclet bajo, la ecuación de convección-difusión también presenta una singularidad a una distancia infinita (donde normalmente se debería colocar la condición de contorno de campo lejano ) debido a que el campo de flujo es lineal en la separación entre partículas. Este problema se puede solucionar con una transformada espacial de Fourier como lo muestra Jan Dhont. ^[13] Alessio Zaccone y sus compañeros de trabajo desarrollaron un enfoque diferente para resolver este problema y consiste en colocar la condición de frontera justo en la distancia de la capa límite, al asumir (en una aproximación de primer orden) un valor constante de la función de distribución de pares en la capa exterior debido a la convección es dominante allí. Esto conduce a una teoría aproximada para la tasa de encuentro de dos partículas coloides que interactúan en un campo de flujo lineal que concuerda con la solución numérica completa. ^[14] Cuando el número de Péclet es significativamente mayor que uno, la singularidad en la separación infinita ya no ocurre y el método de asintóticas emparejadas se puede aplicar para construir la solución completa para la función de distribución de pares en todo el dominio. ^{[15] [16]}

Ver también

• Análisis asintótico
• Análisis a múltiples escalas
• Asintóticas de energía de activación.

Referencias

1. O'Malley, Robert E. (2014), O'Malley, Robert E. (ed.), "El método de expansiones asintóticas emparejadas y sus generalizaciones", Desarrollos históricos en perturbaciones singulares , Cham: Springer International Publishing, págs. 53–121, doi :10.1007/978-3-319-11924-3_3, ISBN 978-3-319-11924-3, consultado el 4 de mayo de 2023
2. RB Dingle (1973), Expansiones asintóticas: su derivación e interpretación , Academic Press .
3. Verhulst, F. (2005). Métodos y aplicaciones de perturbaciones singulares: capas límite y dinámica de múltiples escalas de tiempo . Saltador. ISBN 0-387-22966-3.
4. Nayfeh, AH (2000). Métodos de perturbación . Biblioteca de clásicos de Wiley. Wiley-Interscience. ISBN 978-0-471-39917-9.
5. Kevorkian, J.; Cole, JD (1996). "Métodos de escala múltiple y perturbación singular" . Saltador. ISBN 0-387-94202-5.
6. Doblador, CM; Orszag, SA (1999). Métodos matemáticos avanzados para científicos e ingenieros . Saltador. ISBN 978-0-387-98931-0.
7. Hinch, John (1991). Métodos de perturbación . Prensa de la Universidad de Cambridge .
8. RB Dingle y HJW Müller, J. reine angew. Matemáticas. 211 (1962) 11-32 y 216 (1964) 123-133; HJW Müller, J. reina angew. Matemáticas. 211 (1962) 179-190.
9. HJW Müller, Mathematische Nachrichten 31 (1966) 89-101, 32 (1966) 49-62, 32 (1966) 157-172.
10. HJW Müller, J. reine angew. Matemáticas. 211 (1962) 33-47.
11. HJW Müller, J. reine angew. Matemáticas. 212 (1963) 26-48.
12. HJW Müller-Kirsten (2012), Introducción a la mecánica cuántica: ecuación de Schrödinger e integral de ruta , 2ª ed., World Scientific , ISBN 978-9814397742 . Capítulo 18 sobre potenciales anarmónicos. 
13. Introducción a la dinámica de los coloides por JKG Dhont, enlace de libros de Google
14. Zaccone, A.; Gentili, D.; Wu, H.; Morbidelli, M. (2009). "Teoría de los procesos de velocidad activada bajo cizallamiento con aplicación a la agregación de coloides inducida por cizallamiento". Revisión física E. 80 (5): 051404. arXiv : 0906.4879 . Código Bib : 2009PhRvE..80e1404Z. doi : 10.1103/PhysRevE.80.051404. hdl : 2434/653702 . PMID  20364982. S2CID  22763509.
15. Banetta, L.; Zaccone, A. (2019). "Función de distribución radial de fluidos de Lennard-Jones en flujos de corte de asintóticos intermedios". Revisión física E. 99 (5): 052606. arXiv : 1901.05175 . Código Bib : 2019PhRvE..99e2606B. doi : 10.1103/PhysRevE.99.052606. PMID  31212460. S2CID  119011235.
16. Banetta, L.; Zaccone, A. (2020). "Función de correlación de pares de sistemas coloidales con carga estabilizada en condiciones de corte". Ciencia de coloides y polímeros . 298 (7): 761–771. arXiv : 2006.00246 . doi : 10.1007/s00396-020-04609-4 .