Los algoritmos de combinación son una familia de algoritmos que toman múltiples listas ordenadas como entrada y producen una única lista como salida, que contiene todos los elementos de las listas de entrada en orden ordenado. Estos algoritmos se utilizan como subrutinas en varios algoritmos de ordenación , el más famoso de los cuales es el algoritmo de combinación .
El algoritmo de combinación desempeña un papel fundamental en el algoritmo de ordenación por combinación , un algoritmo de ordenación basado en la comparación . Conceptualmente, el algoritmo de ordenación por combinación consta de dos pasos:
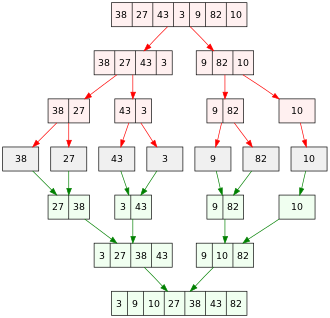
El algoritmo de fusión se utiliza repetidamente en el algoritmo de ordenación por fusión.
En la ilustración se muestra un ejemplo de ordenación por fusión. Comienza con una matriz desordenada de 7 números enteros. La matriz se divide en 7 particiones; cada partición contiene 1 elemento y se ordena. Las particiones ordenadas se fusionan para producir particiones más grandes y ordenadas, hasta que solo queda una partición, la matriz ordenada.
La fusión de dos listas ordenadas en una se puede realizar en tiempo lineal y en espacio lineal o constante (según el modelo de acceso a datos). El siguiente pseudocódigo demuestra un algoritmo que fusiona las listas de entrada (ya sean listas enlazadas o matrices ) A y B en una nueva lista C. [1] [2] : 104 La función head produce el primer elemento de una lista; " eliminar " un elemento significa quitarlo de su lista, normalmente incrementando un puntero o índice.
algoritmo merge(A, B) es entradas A, B : lista devuelve lista C := nueva lista vacía mientras A no esté vacío y B no esté vacío, si cabeza (A) ≤ cabeza(B) entonces añadir encabezado(A) a C dejar caer la cabeza de A demás añadir encabezado(B) a C dejar caer la cabeza de B // En este momento, A o B están vacíos. Queda por vaciar la otra lista de entrada. mientras A no esté vacía, hazlo añadir encabezado(A) a C dejar caer la cabeza de A mientras B no esté vacío, hazlo añadir encabezado(B) a C dejar caer la cabeza de B devolver C
Cuando las entradas son listas enlazadas, este algoritmo se puede implementar para utilizar sólo una cantidad constante de espacio de trabajo; los punteros en los nodos de las listas se pueden reutilizar para la contabilidad y para construir la lista fusionada final.
En el algoritmo de ordenamiento por fusión, esta subrutina se utiliza normalmente para fusionar dos submatrices A[lo..mid] , A[mid+1..hi] de una única matriz A . Esto se puede hacer copiando las submatrices en una matriz temporal y aplicando después el algoritmo de fusión anterior. [1] Se puede evitar la asignación de una matriz temporal, pero a expensas de la velocidad y la facilidad de programación. Se han ideado varios algoritmos de fusión in situ, [3] a veces sacrificando el límite de tiempo lineal para producir un algoritmo O ( n log n ) ; [4] consulte Ordenamiento por fusión § Variantes para obtener más información.
La fusión de k vías generaliza la fusión binaria a un número arbitrario k de listas de entrada ordenadas. Las aplicaciones de la fusión de k vías surgen en varios algoritmos de ordenamiento, incluyendo el ordenamiento por paciencia [5] y un algoritmo de ordenamiento externo que divide su entrada en k = 1/METRO − 1 bloques que caben en la memoria, los ordena uno por uno y luego fusiona estos bloques. [2] : 119–120
Existen varias soluciones para este problema. Una solución simple es hacer un bucle sobre las k listas para seleccionar el elemento mínimo cada vez y repetir este bucle hasta que todas las listas estén vacías:
En el peor de los casos , este algoritmo realiza ( k −1)( n − a/2) comparaciones de elementos para realizar su trabajo si hay un total de n elementos en las listas. [6] Se puede mejorar almacenando las listas en una cola de prioridad ( min-heap ) codificada por su primer elemento:
Ahora es posible buscar el siguiente elemento más pequeño que se va a generar (find-min) y restaurar el orden del montón en tiempo O (log k ) (más específicamente, 2⌊log k ⌋ comparaciones [6] ), y el problema completo se puede resolver en tiempo O ( n log k ) (aproximadamente 2n ⌊log k ⌋ comparaciones). [6] [2] : 119–120
Un tercer algoritmo para el problema es una solución de divide y vencerás que se basa en el algoritmo de fusión binaria:
Cuando las listas de entrada de este algoritmo se ordenan por longitud, la más corta primero, requiere menos de n ⌈log k ⌉ comparaciones, es decir, menos de la mitad del número utilizado por el algoritmo basado en montón; en la práctica, puede ser tan rápido o lento como el algoritmo basado en montón. [6]
Una versión paralela del algoritmo de fusión binaria puede servir como un bloque de construcción de una ordenación por fusión paralela . El siguiente pseudocódigo demuestra este algoritmo en un estilo de divide y vencerás paralelo (adaptado de Cormen et al. [7] : 800 ). Opera en dos matrices ordenadas A y B y escribe la salida ordenada en la matriz C . La notación A[i...j] denota la parte de A desde el índice i hasta el j , exclusivo.
El algoritmo merge(A[i...j], B[k...ℓ], C[p...q]) son entradas A, B, C: matriz i, j, k, ℓ, p, q: índices sea m = j - i, n = ℓ - k si m < n entonces intercambia A y B // asegúrate de que A sea la matriz más grande: i, j todavía pertenecen a A; k, ℓ a B intercambiar m y n si m ≤ 0 entonces retorna // caso base, nada que fusionar sea r = ⌊(i + j)/2⌋ sea s = búsqueda binaria(A[r], B[k...ℓ]) sea t = p + (r - i) + (s - k) C[t] = A[r] en paralelo hacer fusionar(A[i...r], B[k...s], C[p...t]) fusionar(A[r+1...j], B[s...ℓ], C[t+1...q])
El algoritmo opera dividiendo A o B , el que sea mayor, en mitades (casi) iguales. Luego divide la otra matriz en una parte con valores menores que el punto medio de la primera y una parte con valores mayores o iguales. (La subrutina de búsqueda binaria devuelve el índice en B donde A [ r ] estaría, si estuviera en B ; que siempre es un número entre k y ℓ .) Finalmente, cada par de mitades se fusiona recursivamente y, dado que las llamadas recursivas son independientes entre sí, se pueden realizar en paralelo. Se ha demostrado que el enfoque híbrido, donde se utiliza un algoritmo serial para el caso base de recursión, funciona bien en la práctica [8].
El trabajo realizado por el algoritmo para dos matrices que contienen un total de n elementos, es decir, el tiempo de ejecución de una versión serial de la misma, es O ( n ) . Esto es óptimo ya que se deben copiar n elementos en C . Para calcular el lapso del algoritmo, es necesario derivar una relación de recurrencia . Como las dos llamadas recursivas de merge son en paralelo, solo se debe considerar la más costosa de las dos llamadas. En el peor de los casos, el número máximo de elementos en una de las llamadas recursivas es como máximo ya que la matriz con más elementos está perfectamente dividida a la mitad. Sumando el costo de la Búsqueda Binaria, obtenemos esta recurrencia como límite superior:
La solución es , lo que significa que lleva ese tiempo en una máquina ideal con un número ilimitado de procesadores. [7] : 801–802
Nota: La rutina no es estable : si se separan elementos iguales dividiendo A y B , se intercalarán en C ; además, intercambiar A y B destruirá el orden si los elementos iguales se distribuyen entre ambas matrices de entrada. Como resultado, cuando se utiliza para ordenar, este algoritmo produce una clasificación que no es estable.
También existen algoritmos que introducen paralelismo en una única instancia de fusión de dos listas ordenadas. Estos pueden utilizarse en matrices de puertas programables en campo ( FPGA ), circuitos de ordenación especializados, así como en procesadores modernos con instrucciones SIMD (instrucción única y múltiples datos ).
Los algoritmos paralelos existentes se basan en modificaciones de la parte de fusión del clasificador bitónico o del mergesort impar-par . [9] En 2018, Saitoh M. et al. introdujeron MMS [10] para FPGAs, que se centró en eliminar una ruta de datos de retroalimentación de múltiples ciclos que impedía una canalización eficiente en hardware. También en 2018, Papaphilippou P. et al. introdujeron FLiMS [9] que mejoró la utilización y el rendimiento del hardware al requerir solo etapas de canalización de unidades de comparación e intercambio P/2 para fusionarse con un paralelismo de P elementos por ciclo de FPGA.
Algunos lenguajes de computadora proporcionan soporte integrado o de biblioteca para fusionar colecciones ordenadas .
La biblioteca de plantillas estándar de C++ tiene la función std::merge , que fusiona dos rangos ordenados de iteradores , y std::inplace_merge , que fusiona dos rangos ordenados consecutivos in situ . Además, la clase std::list (lista enlazada) tiene su propio método de fusión que fusiona otra lista en sí misma. El tipo de los elementos fusionados debe admitir el operador menor que ( < ), o debe proporcionarse con un comparador personalizado.
C++17 permite diferentes políticas de ejecución, a saber, secuencial, paralela y paralela-no secuencial. [11]
La biblioteca estándar de Python (desde 2.6) también tiene una función de fusión en el módulo heapq , que toma múltiples iterables ordenados y los fusiona en un solo iterador. [12]