Curva de retención de agua

Curva de retención de agua para arena (Ss), limo o franco arcilloso (Uu), franco limoso o arcilla (Lu) y arcilla o turba (Tt).

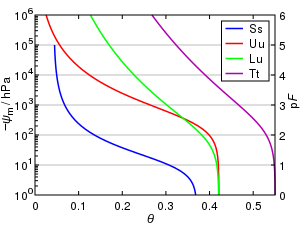
La curva de retención de agua es la relación entre el contenido de agua , θ , y el potencial hídrico del suelo , ψ. Esta curva es característica de diferentes tipos de suelo y también se denomina característica de humedad del suelo .

Se utiliza para predecir el almacenamiento de agua en el suelo, el suministro de agua a las plantas ( capacidad de campo ) y la estabilidad de los agregados del suelo . Debido al efecto histérico del agua que llena y drena los poros, se pueden distinguir diferentes curvas de humectación y secado.

Las características generales de una curva de retención de agua se pueden ver en la figura, en la que el contenido de agua en volumen, θ , se representa gráficamente frente al potencial mátrico, . A potenciales cercanos a cero, un suelo está cerca de la saturación y el agua se mantiene en el suelo principalmente por fuerzas capilares. A medida que θ disminuye, la unión del agua se hace más fuerte y, a potenciales pequeños (más negativos, acercándose al punto de marchitamiento ) el agua está fuertemente unida en los poros más pequeños, en los puntos de contacto entre los granos y como películas unidas por fuerzas de adsorción alrededor de las partículas. ${\displaystyle \Psi _{m}}$

Los suelos arenosos implican principalmente unión capilar y, por lo tanto, liberarán la mayor parte del agua a potenciales más altos, mientras que los suelos arcillosos, con unión adhesiva y osmótica, liberarán agua a potenciales más bajos (más negativos). En cualquier potencial dado, los suelos turbosos generalmente mostrarán contenidos de humedad mucho más altos que los suelos arcillosos, que se esperaría que retengan más agua que los suelos arenosos. La capacidad de retención de agua de cualquier suelo se debe a la porosidad y la naturaleza de la unión en el suelo.

Modelos de curvas

La forma de las curvas de retención de agua se puede caracterizar mediante varios modelos, uno de ellos conocido como modelo de Van Genuchten: ^[1]

${\displaystyle \theta (\psi )=\theta _{r}+{\frac {\theta _{s}-\theta _{r}}{\left[1+(\alpha |\psi |)^{n}\right]^{1-1/n}}}}$

dónde

${\displaystyle \theta (\psi )}$es la curva de retención de agua [L ³ L ⁻³ ];

${\displaystyle |\psi |}$es la presión de succión ([L] o cm de agua);

${\displaystyle \theta _{s}}$contenido de agua saturada [L ³ L ⁻³ ];

${\displaystyle \theta _{r}}$contenido de agua residual [L ³ L ⁻³ ];

${\displaystyle \alpha }$está relacionada con la inversa de la succión de entrada de aire, ([L ⁻¹ ], o cm ⁻¹ ); y, ${\displaystyle \alpha >0}$

${\displaystyle n}$es una medida de la distribución del tamaño de los poros (adimensional). ${\displaystyle n>1}$

Con base en esta parametrización se desarrolló un modelo de predicción de la forma de la relación conductividad hidráulica no saturada - saturación - presión. ^[2]

Historia

En 1907, Edgar Buckingham creó la primera curva de retención de agua. ^[2] Se midió y elaboró ​​para seis suelos con texturas que variaban desde arena hasta arcilla. Los datos se obtuvieron a partir de experimentos realizados en columnas de suelo de 48 pulgadas de alto, donde se mantenía un nivel de agua constante aproximadamente 2 pulgadas por encima del fondo mediante la adición periódica de agua desde un tubo lateral. Los extremos superiores estaban cerrados para evitar la evaporación.

Método

Los parámetros de Van Genuchten ( y ) se pueden determinar mediante pruebas de campo o de laboratorio. Uno de los métodos es el método de perfil instantáneo, ^[3] donde el contenido de agua (o saturación efectiva ) se determina para una serie de mediciones de presión de succión . Debido a la no linealidad de la ecuación, se pueden utilizar técnicas numéricas como el método de mínimos cuadrados no lineales para resolver los parámetros de van Genuchten. ^{[4] [5]} La precisión de los parámetros estimados dependerá de la calidad del conjunto de datos adquiridos ( y ). Cuando las curvas de retención de agua se ajustan con mínimos cuadrados no lineales, puede ocurrir una sobreestimación o subestimación estructural. En estos casos, la representación de las curvas de retención de agua se puede mejorar en términos de precisión e incertidumbre aplicando la regresión del proceso gaussiano a los residuos que se obtienen después de los mínimos cuadrados no lineales. Esto se debe principalmente a la correlación entre los puntos de datos, que se explica con la regresión del proceso gaussiano a través de la función kernel. ^[6] ${\displaystyle \alpha }$ ${\displaystyle n}$ ${\displaystyle \theta }$ ${\displaystyle Se}$ ${\displaystyle \psi }$ ${\displaystyle \theta }$ ${\displaystyle \psi }$

Véase también

• Agua del suelo (retención)

Referencias

1. van Genuchten, M.Th. (1980). "Una ecuación de forma cerrada para predecir la conductividad hidráulica de suelos no saturados". Revista de la Sociedad Americana de Ciencias del Suelo . 44 (5): 892–898. Bibcode :1980SSASJ..44..892V. doi :10.2136/sssaj1980.03615995004400050002x. hdl :10338.dmlcz/141699.
2. Buckingham, Edgar (1907), Estudios sobre el movimiento de la humedad del suelo, Bureau of Soils, Bulletin, vol. 38, Washington, DC: Departamento de Agricultura de los Estados Unidos
3. Watson, KK. (1966). "Un método de perfil instantáneo para determinar la conductividad hidráulica de materiales porosos no saturados". Investigación de recursos hídricos . 2 (4): 709–715. Bibcode :1966WRR.....2..709W. doi :10.1029/WR002i004p00709.
4. Seki, K. (2007). "Ajuste SWRC: un programa de ajuste no lineal con una curva de retención de agua para suelos con estructura de poros unimodal y bimodal" (PDF) . Discusiones sobre hidrología y ciencias del sistema terrestre . 4 (1): 407–437. Bibcode :2007HESSD...4..407S. doi : 10.5194/hessd-4-407-2007 .
5. Chou, TK (2016). "Una aplicación GUI gratuita para resolver los parámetros de van Genuchten mediante la minimización de mínimos cuadrados no lineales y el ajuste de curvas" (PDF) . www.cmcsjc.com . Enero: 1–5. Archivado desde el original (PDF) el 4 de marzo de 2016.
6. Yousef, B. (junio de 2019). Modelos de regresión de procesos gaussianos para predecir curvas de retención de agua: aplicación de técnicas de aprendizaje automático para modelar la incertidumbre en curvas hidráulicas. Recuperado del repositorio de la Universidad Tecnológica de Delft.

• Brady, NC (1999). La naturaleza y las propiedades de los suelos (12.ª ed.). Upper Saddle River, NJ: Prentice-Hall. pp. 183–9. ISBN 0-13-852444-0.

Enlaces externos

• Base de datos del modelo UNSODA de propiedades hidráulicas de suelos no saturados (visor UNSODA)
• SWRC Fit ajusta los modelos hidráulicos del suelo a los datos de retención de agua del suelo