Frecuencia de corte

Límite de respuesta de frecuencia

Función de transferencia de magnitud de un filtro de paso de banda con una frecuencia de corte inferior de 3 dB f ₁ y una frecuencia de corte superior de 3 dB f ₂

Diagrama de Bode (un diagrama de respuesta de frecuencia logarítmica ) de cualquier filtro de paso bajo de primer orden con una frecuencia de corte normalizada en =1 y una banda de paso de ganancia unitaria (0 dB). ${\displaystyle \omega }$

En física e ingeniería eléctrica , una frecuencia de corte , frecuencia de esquina o frecuencia de ruptura es un límite en la respuesta de frecuencia de un sistema en el que la energía que fluye a través del sistema comienza a reducirse ( atenuarse o reflejarse) en lugar de pasar a través de él.

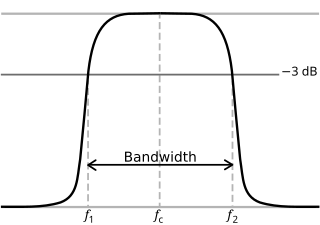
Por lo general, en sistemas electrónicos como filtros y canales de comunicación , la frecuencia de corte se aplica a un borde en una característica de paso bajo , paso alto , paso de banda o banda eliminada : una frecuencia que caracteriza un límite entre una banda de paso y una banda eliminada . A veces se toma como el punto en la respuesta del filtro donde una banda de transición y una banda de paso se encuentran, por ejemplo, como se define por un punto de media potencia (una frecuencia para la cual la salida del circuito es aproximadamente −3,01  dB del valor nominal de la banda de paso). Alternativamente, una frecuencia de esquina de banda eliminada se puede especificar como un punto donde una banda de transición y una banda eliminada se encuentran: una frecuencia para la cual la atenuación es mayor que la atenuación de banda eliminada requerida, que, por ejemplo, puede ser 30 dB o 100 dB.

En el caso de una guía de ondas o una antena , las frecuencias de corte corresponden a las longitudes de onda de corte inferior y superior .

Electrónica

En electrónica , la frecuencia de corte o frecuencia de esquina es la frecuencia por encima o por debajo de la cual la potencia de salida de un circuito , como una línea , un amplificador o un filtro electrónico , ha caído a una proporción dada de la potencia en la banda de paso . Lo más frecuente es que esta proporción sea la mitad de la potencia de la banda de paso, también denominada punto de 3  dB , ya que una caída de 3 dB corresponde aproximadamente a la mitad de la potencia. Como relación de voltaje, esta es una caída de del voltaje de la banda de paso. ^[1] También pueden ser relevantes otras relaciones además del punto de 3 dB, por ejemplo, consulte el § Filtros de Chebyshev a continuación. Lejos de la frecuencia de corte en la banda de transición, la tasa de aumento de la atenuación ( roll-off ) con el logaritmo de la frecuencia es asintótica a una constante. Para una red de primer orden , el roll-off es de −20 dB por década (aproximadamente −6 dB por octava ). ${\textstyle {\sqrt {1/2}}\ \approx \ 0.707}$

Ejemplo de función de transferencia unipolar

La función de transferencia para el filtro de paso bajo más simple tiene un solo polo en s = −1/ α . La magnitud de esta función en el plano jω es $${\displaystyle H(s)={\frac {1}{1+\alpha s}},}$$ $${\displaystyle \left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.}$$

En el punto de corte $${\displaystyle \left|H(j\omega _{\mathrm {c} })\right|={\frac {1}{\sqrt {2}}}={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}.}$$

Por lo tanto, la frecuencia de corte viene dada por $${\displaystyle \omega _{\mathrm {c} }={\frac {1}{\alpha }}.}$$

Donde s es la variable del plano s , ω es la frecuencia angular y j es la unidad imaginaria .

Filtros de Chebyshev

En ocasiones, otras relaciones son más convenientes que el punto de 3 dB. Por ejemplo, en el caso del filtro Chebyshev, es habitual definir la frecuencia de corte como el punto después del último pico en la respuesta de frecuencia en el que el nivel ha caído al valor de diseño de la ondulación de la banda de paso. El diseñador puede establecer la cantidad de ondulación en esta clase de filtro en cualquier valor deseado, por lo que la relación utilizada podría ser cualquier valor. ^[2]

Comunicaciones por radio

En la comunicación por radio , la comunicación por ondas ionosféricas es una técnica en la que las ondas de radio se transmiten en un ángulo hacia el cielo y se reflejan de vuelta a la Tierra por capas de partículas cargadas en la ionosfera . En este contexto, el término frecuencia de corte se refiere a la frecuencia máxima utilizable , la frecuencia por encima de la cual una onda de radio no se refleja en la ionosfera en el ángulo de incidencia necesario para la transmisión entre dos puntos específicos por reflexión desde la capa.

Guías de ondas

La frecuencia de corte de una guía de ondas electromagnéticas es la frecuencia más baja para la cual un modo se propagará en ella. En fibra óptica , es más común considerar la longitud de onda de corte , la longitud de onda máxima que se propagará en una fibra óptica o guía de ondas . La frecuencia de corte se encuentra con la ecuación característica de la ecuación de Helmholtz para ondas electromagnéticas, que se deriva de la ecuación de onda electromagnética al establecer el número de onda longitudinal igual a cero y resolver para la frecuencia. Por lo tanto, cualquier frecuencia de excitación menor que la frecuencia de corte se atenuará, en lugar de propagarse. La siguiente derivación supone paredes sin pérdidas. El valor de c, la velocidad de la luz , debe tomarse como la velocidad de grupo de la luz en cualquier material que llene la guía de ondas.

Para una guía de ondas rectangular, la frecuencia de corte es donde son los números de modo para los lados del rectángulo de longitud y respectivamente. Para los modos TE, (pero no está permitido), mientras que para los modos TM . $${\displaystyle \omega _{c}=c{\sqrt {\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}}},}$$ ${\displaystyle m,n\geq 0}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle m,n\geq 0}$ ${\displaystyle m=n=0}$ ${\displaystyle m,n\geq 1}$

La frecuencia de corte del modo TM ₀₁ (el siguiente más alto desde el modo dominante TE ₁₁ ) en una guía de onda de sección transversal circular (el modo transversal-magnético sin dependencia angular y con la menor dependencia radial) está dada por donde es el radio de la guía de onda, y es la primera raíz de , la función de Bessel de primer tipo de orden 1. $${\displaystyle \omega _{c}=c{\frac {\chi _{01}}{r}}=c{\frac {2.4048}{r}},}$$ ${\displaystyle r}$ ${\displaystyle \chi _{01}}$ ${\displaystyle J_{0}(r)}$

La frecuencia de corte del modo dominante TE ₁₁ está dada por ^[3] $${\displaystyle \omega _{c}=c{\frac {\chi _{11}}{r}}=c{\frac {1.8412}{r}}}$$

Sin embargo, la frecuencia de corte del modo dominante se puede reducir mediante la introducción de un deflector dentro de la guía de ondas de sección transversal circular. ^[4] Para una fibra óptica monomodo , la longitud de onda de corte es la longitud de onda en la que la frecuencia normalizada es aproximadamente igual a 2,405.

Análisis matemático

El punto de partida es la ecuación de onda (que se deriva de las ecuaciones de Maxwell ), que se convierte en una ecuación de Helmholtz al considerar solo funciones de la forma Sustituyendo y evaluando la derivada temporal se obtiene La función aquí se refiere a cualquier campo (el campo eléctrico o el campo magnético) que no tenga un componente vectorial en la dirección longitudinal: el campo "transversal". Es una propiedad de todos los modos propios de la guía de ondas electromagnética que al menos uno de los dos campos sea transversal. El eje z se define como a lo largo del eje de la guía de ondas. $${\displaystyle \left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial {t}^{2}}}\right)\psi (\mathbf {r} ,t)=0,}$$ $${\displaystyle \psi (x,y,z,t)=\psi (x,y,z)e^{i\omega t}.}$$ $${\displaystyle \left(\nabla ^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\psi (x,y,z)=0.}$$ ${\displaystyle \psi }$

La derivada "longitudinal" en el laplaciano se puede reducir aún más considerando solo funciones de la forma donde es el número de onda longitudinal , lo que da como resultado donde el subíndice T indica un laplaciano transversal bidimensional. El paso final depende de la geometría de la guía de ondas. La geometría más fácil de resolver es la guía de ondas rectangular. En ese caso, el resto del laplaciano se puede evaluar en su ecuación característica considerando soluciones de la forma Por lo tanto, para la guía rectangular se evalúa el laplaciano y llegamos a Los números de onda transversales se pueden especificar a partir de las condiciones de contorno de onda estacionaria para una sección transversal de geometría rectangular con dimensiones a y b : donde n y m son los dos números enteros que representan un modo propio específico. Realizando la sustitución final, obtenemos que es la relación de dispersión en la guía de ondas rectangular. La frecuencia de corte es la frecuencia crítica entre la propagación y la atenuación, que corresponde a la frecuencia en la que el número de onda longitudinal es cero. Está dada por Las ecuaciones de onda también son válidas por debajo de la frecuencia de corte, donde el número de onda longitudinal es imaginario. En este caso, el campo decae exponencialmente a lo largo del eje de la guía de ondas y la onda es, por tanto, evanescente . $${\displaystyle \psi (x,y,z,t)=\psi (x,y)e^{i\left(\omega t-k_{z}z\right)},}$$ ${\displaystyle k_{z}}$ $${\displaystyle \left(\nabla _{T}^{2}-k_{z}^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\psi (x,y,z)=0,}$$ $${\displaystyle \psi (x,y,z,t)=\psi _{0}e^{i\left(\omega t-k_{z}z-k_{x}x-k_{y}y\right)}.}$$ $${\displaystyle {\frac {\omega ^{2}}{c^{2}}}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}$$ $${\displaystyle k_{x}={\frac {n\pi }{a}},}$$ $${\displaystyle k_{y}={\frac {m\pi }{b}},}$$ $${\displaystyle {\frac {\omega ^{2}}{c^{2}}}=\left({\frac {n\pi }{a}}\right)^{2}+\left({\frac {m\pi }{b}}\right)^{2}+k_{z}^{2},}$$ ${\displaystyle \omega _{c}}$ ${\displaystyle k_{z}}$ $${\displaystyle \omega _{c}=c{\sqrt {\left({\frac {n\pi }{a}}\right)^{2}+\left({\frac {m\pi }{b}}\right)^{2}}}}$$

Véase también

• Ancho completo a la mitad máximo
• Filtro de paso alto
• Efecto Miller
• Frecuencia de corte espacial (en sistemas ópticos)
• Constante de tiempo

Referencias

1. Van Valkenburg, ME (1974). Análisis de red (3ª ed.). págs. 383–384. ISBN 0-13-611095-9. Consultado el 22 de junio de 2008 .
2. Mathaei, Young, Jones Filtros de microondas, redes de adaptación de impedancia y estructuras de acoplamiento , págs. 85-86, McGraw-Hill 1964.
3. Hunter, IC (2001). Teoría y diseño de filtros de microondas. Institution of Electrical Engineers. Londres: Institution of Electrical Engineers. pág. 214. ISBN 978-0-86341-253-0.OCLC 505848355  .
4. Modi, Anuj Y.; Balanis, Constantine A. (1 de marzo de 2016). "Deflector PEC-PMC dentro de una guía de ondas de sección transversal circular para la reducción de la frecuencia de corte". IEEE Microwave and Wireless Components Letters . 26 (3): 171–173. doi :10.1109/LMWC.2016.2524529. ISSN  1531-1309. S2CID  9594124.

•  Este artículo incorpora material de dominio público de la Norma Federal 1037C. Administración de Servicios Generales . Archivado desde el original el 22 de enero de 2022. (en apoyo de MIL-STD-188 ).

Enlaces externos

• Cálculo de la frecuencia central con media geométrica y comparación con la solución de media aritmética
• Conversión de la frecuencia de corte fc y la constante de tiempo τ
• Definición matemática e información sobre las funciones de Bessel