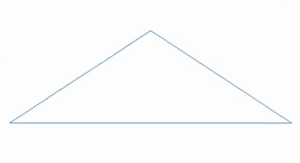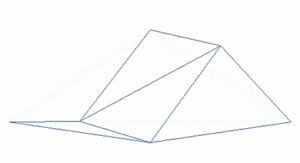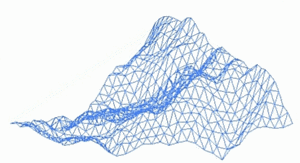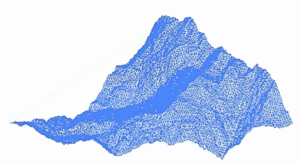
Un paisaje fractal o superficie fractal se genera utilizando un algoritmo estocástico diseñado para producir un comportamiento fractal que imita la apariencia del terreno natural . En otras palabras, la superficie resultante del procedimiento no es determinista, sino más bien una superficie aleatoria que exhibe un comportamiento fractal. [1]
Muchos fenómenos naturales presentan alguna forma de autosimilitud estadística que puede ser modelada por superficies fractales . [2] Además, las variaciones en la textura de la superficie proporcionan importantes pistas visuales sobre la orientación y las pendientes de las superficies, y el uso de patrones fractales casi autosimilares puede ayudar a crear efectos visuales de apariencia natural. [3] El modelado de las superficies rugosas de la Tierra a través del movimiento browniano fraccional fue propuesto por primera vez por Benoit Mandelbrot . [4]
Dado que el resultado previsto del proceso es producir un paisaje, en lugar de una función matemática, con frecuencia se aplican a dichos paisajes procesos que pueden afectar la estacionariedad e incluso el comportamiento fractal general de dicha superficie , con el fin de producir un paisaje más convincente.
Según RR Shearer , la generación de superficies y paisajes de aspecto natural fue un punto de inflexión importante en la historia del arte, donde la distinción entre imágenes geométricas generadas por computadora y arte natural hecho por el hombre se volvió borrosa. [5] El primer uso de un paisaje generado por fractales en una película fue en 1982 para la película Star Trek II: La ira de Khan . Loren Carpenter refinó las técnicas de Mandelbrot para crear un paisaje alienígena. [6]



El hecho de que los paisajes naturales se comporten de manera fractal o no ha sido objeto de algunas investigaciones. Técnicamente hablando, cualquier superficie en el espacio tridimensional tiene una dimensión topológica de 2 y, por lo tanto, cualquier superficie fractal en el espacio tridimensional tiene una dimensión de Hausdorff entre 2 y 3. [7] Sin embargo, los paisajes reales tienen un comportamiento variable a diferentes escalas. Esto significa que un intento de calcular la dimensión fractal "general" de un paisaje real puede dar como resultado medidas de dimensión fractal negativa o de dimensión fractal por encima de 3. En particular, muchos estudios de fenómenos naturales, incluso aquellos que comúnmente se cree que exhiben un comportamiento fractal, no lo hacen en más de unos pocos órdenes de magnitud. Por ejemplo, el examen de Richardson de la costa occidental de Gran Bretaña mostró un comportamiento fractal de la costa en solo dos órdenes de magnitud. [8] En general, no hay razón para suponer que los procesos geológicos que dan forma al terreno a gran escala (por ejemplo, la tectónica de placas ) exhiban el mismo comportamiento matemático que los que dan forma al terreno a escalas más pequeñas (por ejemplo, el deslizamiento del suelo ).
Los paisajes reales también tienen un comportamiento estadístico variable de un lugar a otro, por lo que, por ejemplo, las playas de arena no exhiben las mismas propiedades fractales que las cadenas montañosas. Sin embargo, una función fractal es estadísticamente estacionaria, lo que significa que sus propiedades estadísticas en masa son las mismas en todas partes. Por lo tanto, cualquier enfoque real para modelar paisajes requiere la capacidad de modular el comportamiento fractal espacialmente. Además, los paisajes reales tienen muy pocos mínimos naturales (la mayoría de estos son lagos), mientras que una función fractal tiene tantos mínimos como máximos, en promedio. Los paisajes reales también tienen características que se originan con el flujo de agua y hielo sobre su superficie, que los fractales simples no pueden modelar. [9]
Debido a estas consideraciones, las funciones fractales simples suelen ser inadecuadas para modelar paisajes. Las técnicas más sofisticadas (conocidas como técnicas "multifractales") utilizan diferentes dimensiones fractales para diferentes escalas y, por lo tanto, pueden modelar mejor el comportamiento del espectro de frecuencias de paisajes reales [10].
Una forma de crear un paisaje de este tipo es emplear el algoritmo de desplazamiento aleatorio del punto medio , en el que un cuadrado se subdivide en cuatro cuadrados iguales más pequeños y el punto central se desplaza verticalmente por una cantidad aleatoria. El proceso se repite en los cuatro cuadrados nuevos, y así sucesivamente, hasta que se alcanza el nivel de detalle deseado . Existen muchos procedimientos fractales (como la combinación de múltiples octavas de ruido Simplex ) capaces de crear datos de terreno; sin embargo, el término "paisaje fractal" se ha vuelto más genérico con el tiempo.
Las plantas fractales se pueden generar de forma procedimental utilizando sistemas L en escenas generadas por computadora. [11]