Gramática formal

Un ejemplo de una gramática formal con una oración analizada. Las gramáticas formales constan de un conjunto de símbolos no terminales, símbolos terminales, reglas de producción y un símbolo de inicio designado.

Estructura de un lenguaje formal

Una gramática formal describe qué cadenas de un alfabeto de un lenguaje formal son válidas según la sintaxis del lenguaje . Una gramática no describe el significado de las cadenas ni lo que se puede hacer con ellas en cualquier contexto, solo su forma. Una gramática formal se define como un conjunto de reglas de producción para dichas cadenas en un lenguaje formal.

La teoría del lenguaje formal, disciplina que estudia las gramáticas y los lenguajes formales, es una rama de las matemáticas aplicadas . Sus aplicaciones se encuentran en la informática teórica , la lingüística teórica , la semántica formal , la lógica matemática y otras áreas.

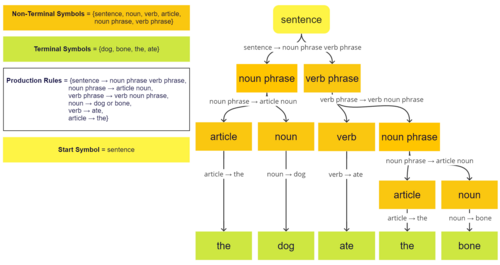
Una gramática formal es un conjunto de reglas para reescribir cadenas, junto con un "símbolo de inicio" a partir del cual comienza la reescritura. Por lo tanto, una gramática suele considerarse como un generador de lenguaje. Sin embargo, a veces también se puede utilizar como base para un " reconocedor ", una función informática que determina si una cadena dada pertenece al lenguaje o es gramaticalmente incorrecta. Para describir dichos reconocedores, la teoría del lenguaje formal utiliza formalismos separados, conocidos como teoría de autómatas . Uno de los resultados interesantes de la teoría de autómatas es que no es posible diseñar un reconocedor para ciertos lenguajes formales. ^[1] El análisis sintáctico es el proceso de reconocer un enunciado (una cadena en los lenguajes naturales) descomponiéndolo en un conjunto de símbolos y analizando cada uno de ellos en relación con la gramática del lenguaje. La mayoría de los lenguajes tienen los significados de sus enunciados estructurados de acuerdo con su sintaxis, una práctica conocida como semántica compositiva . Como resultado, el primer paso para describir el significado de un enunciado en el lenguaje es dividirlo parte por parte y observar su forma analizada (conocida como su árbol de análisis en informática y como su estructura profunda en gramática generativa ).

Ejemplo introductorio

Una gramática consiste principalmente en un conjunto de reglas de producción , reglas de reescritura para transformar cadenas. Cada regla especifica un reemplazo de una cadena particular (su lado izquierdo ) por otra (su lado derecho ). Una regla se puede aplicar a cada cadena que contenga su lado izquierdo y produce una cadena en la que una ocurrencia de ese lado izquierdo ha sido reemplazada por su lado derecho.

A diferencia de un sistema semi-Thue , que está totalmente definido por estas reglas, una gramática distingue además entre dos tipos de símbolos: símbolos no terminales y símbolos terminales ; cada lado izquierdo debe contener al menos un símbolo no terminal. También distingue un símbolo no terminal especial, llamado símbolo de inicio .

El lenguaje generado por la gramática se define como el conjunto de todas las cadenas sin símbolos no terminales que se pueden generar a partir de la cadena que consiste en un único símbolo de inicio mediante la aplicación (posiblemente repetida) de sus reglas de cualquier manera posible. Si existen formas esencialmente diferentes de generar la misma cadena única, se dice que la gramática es ambigua .

En los siguientes ejemplos, los símbolos terminales son a y b , y el símbolo de inicio es S.

Ejemplo 1

Supongamos que tenemos las siguientes reglas de producción:

1. ${\displaystyle S\rightarrow aSb}$

2. ${\displaystyle S\rightarrow ba}$

Entonces empezamos con S y podemos elegir una regla para aplicarle. Si elegimos la regla 1, obtenemos la cadena aSb . Si elegimos la regla 1 de nuevo, reemplazamos S por aSb y obtenemos la cadena aaSbb . Si ahora elegimos la regla 2, reemplazamos S por ba y obtenemos la cadena aababb y listo. Podemos escribir esta serie de elecciones de forma más breve, utilizando símbolos: . ${\displaystyle S\Rightarrow aSb\Rightarrow aaSbb\Rightarrow aababb}$

El lenguaje de la gramática es el conjunto infinito , donde se repite veces (y en particular representa la cantidad de veces que se aplicó la regla de producción 1). Esta gramática es independiente del contexto (solo los no terminales simples aparecen como lados izquierdos) y no tiene ambigüedades. ${\displaystyle \{a^{n}bab^{n}\mid n\geq 0\}=\{ba,abab,aababb,aaababbb,\dotsc \}}$ ${\displaystyle a^{k}}$ ${\displaystyle a}$ ${\displaystyle k}$ ${\displaystyle n}$

Ejemplos 2 y 3

Supongamos que las reglas fueran éstas:

1. ${\displaystyle S\rightarrow a}$

2. ${\displaystyle S\rightarrow SS}$

3. ${\displaystyle aSa\rightarrow b}$

Esta gramática no es libre de contexto debido a la regla 3 y es ambigua debido a las múltiples formas en que se puede usar la regla 2 para generar secuencias de s. ${\displaystyle S}$

Sin embargo, el lenguaje que genera es simplemente el conjunto de todas las cadenas no vacías que consisten en s y/o s. Esto es fácil de ver: para generar a a partir de an , use la regla 2 dos veces para generar , luego la regla 1 dos veces y la regla 3 una vez para producir . Esto significa que podemos generar secuencias no vacías arbitrarias de s y luego reemplazar cada una de ellas con o como queramos. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle S}$ ${\displaystyle SSS}$ ${\displaystyle b}$ ${\displaystyle S}$ ${\displaystyle a}$ ${\displaystyle b}$

Ese mismo lenguaje puede generarse alternativamente mediante una gramática libre de contexto y no ambigua; por ejemplo, la gramática regular con reglas.

1. ${\displaystyle S\rightarrow aS}$

2. ${\displaystyle S\rightarrow bS}$

3. ${\displaystyle S\rightarrow a}$

4. ${\displaystyle S\rightarrow b}$

Definición formal

La sintaxis de las gramáticas

En la formalización clásica de gramáticas generativas propuesta por primera vez por Noam Chomsky en la década de 1950, ^{[2] [3]} una gramática G consta de los siguientes componentes:

• Un conjunto finito N de símbolos no terminales , que es disjunto con las cadenas formadas a partir de G.
• Un conjunto finito de símbolos terminales que es disjunto de N. ${\displaystyle \Sigma }$
• Un conjunto finito P de reglas de producción , cada regla de la forma

${\displaystyle (\Sigma \cup N)^{*}N(\Sigma \cup N)^{*}\rightarrow (\Sigma \cup N)^{*}}$

donde es el operador de estrella de Kleene y denota unión de conjuntos . Es decir, cada regla de producción se asigna de una cadena de símbolos a otra, donde la primera cadena (la "cabeza") contiene un número arbitrario de símbolos siempre que al menos uno de ellos sea no terminal. En el caso de que la segunda cadena (el "cuerpo") consista únicamente en la cadena vacía , es decir, que no contenga ningún símbolo, se puede denotar con una notación especial (a menudo , e o ) para evitar confusiones. ${\displaystyle {*}}$ ${\displaystyle \cup }$ ${\displaystyle \Lambda }$ ${\displaystyle \epsilon }$

• Un símbolo distinguido que es el símbolo de inicio , también llamado símbolo de oración . ${\displaystyle S\in N}$

Una gramática se define formalmente como la tupla . En la literatura, a este tipo de gramática formal se la suele denominar sistema de reescritura o gramática de estructura de frase . ^{[4] [5]} ${\displaystyle (N,\Sigma ,P,S)}$

Algunas construcciones matemáticas relativas a las gramáticas formales

El funcionamiento de una gramática se puede definir en términos de relaciones sobre cadenas:

• Dada una gramática , la relación binaria (pronunciada como "G deriva en un paso") en cadenas en se define por: ${\displaystyle G=(N,\Sigma ,P,S)}$ ${\displaystyle {\underset {G}{\Rightarrow }}}$ ${\displaystyle (\Sigma \cup N)^{*}}$

  ${\displaystyle x{\underset {G}{\Rightarrow }}y\iff \exists u,v,p,q\in (\Sigma \cup N)^{*}:(x=upv)\wedge (p\rightarrow q\in P)\wedge (y=uqv)}$

• La relación (pronunciada como G deriva en cero o más pasos ) se define como el cierre transitivo reflexivo de ${\displaystyle {\overset {*}{\underset {G}{\Rightarrow }}}}$ ${\displaystyle {\underset {G}{\Rightarrow }}}$
• aLa forma oracional es un miembro de que se puede derivar en un número finito de pasos desde el símbolo inicial ; es decir, una forma oracional es un miembro de . Una forma oracional que no contiene símbolos no terminales (es decir, es un miembro de ) se denomina oración . ^[6] ${\displaystyle (\Sigma \cup N)^{*}}$ ${\displaystyle S}$ ${\displaystyle \left\{w\in (\Sigma \cup N)^{*}\mid S{\overset {*}{\underset {G}{\Rightarrow }}}w\right\}}$ ${\displaystyle \Sigma ^{*}}$
• El lenguaje de , denotado como , se define como el conjunto de oraciones construidas por . ${\displaystyle G}$ ${\displaystyle {\boldsymbol {L}}(G)}$ ${\displaystyle G}$

La gramática es efectivamente el sistema semi-Thue , reescribiendo cadenas exactamente de la misma manera; la única diferencia es que distinguimos símbolos no terminales específicos , que deben reescribirse en reglas de reescritura, y solo estamos interesados ​​en reescrituras desde el símbolo de inicio designado a cadenas sin símbolos no terminales. ${\displaystyle G=(N,\Sigma ,P,S)}$ ${\displaystyle (N\cup \Sigma ,P)}$ ${\displaystyle S}$

Ejemplo

Para estos ejemplos, los lenguajes formales se especifican utilizando la notación de construcción de conjuntos .

Considere la gramática donde , , es el símbolo de inicio y consta de las siguientes reglas de producción: ${\displaystyle G}$ ${\displaystyle N=\left\{S,B\right\}}$ ${\displaystyle \Sigma =\left\{a,b,c\right\}}$ ${\displaystyle S}$ ${\displaystyle P}$

1. ${\displaystyle S\rightarrow aBSc}$

2. ${\displaystyle S\rightarrow abc}$

3. ${\displaystyle Ba\rightarrow aB}$

4. ${\displaystyle Bb\rightarrow bb}$

Esta gramática define el lenguaje donde denota una cadena de n ' consecutivos . Por lo tanto, el lenguaje es el conjunto de cadenas que constan de 1 o más ', seguidos por el mismo número de ', seguidos por el mismo número de '. ${\displaystyle L(G)=\left\{a^{n}b^{n}c^{n}\mid n\geq 1\right\}}$ ${\displaystyle a^{n}}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

Algunos ejemplos de la derivación de cadenas son: ${\displaystyle L(G)}$

• ${\displaystyle {\boldsymbol {S}}{\underset {2}{\Rightarrow }}{\boldsymbol {abc}}}$
• ${\displaystyle {\begin{aligned}{\boldsymbol {S}}&{\underset {1}{\Rightarrow }}{\boldsymbol {aBSc}}\\&{\underset {2}{\Rightarrow }}aB{\boldsymbol {abc}}c\\&{\underset {3}{\Rightarrow }}a{\boldsymbol {aB}}bcc\\&{\underset {4}{\Rightarrow }}aa{\boldsymbol {bb}}cc\end{aligned}}}$
• ${\displaystyle {\begin{aligned}{\boldsymbol {S}}&{\underset {1}{\Rightarrow }}{\boldsymbol {aBSc}}{\underset {1}{\Rightarrow }}aB{\boldsymbol {aBSc}}c\\&{\underset {2}{\Rightarrow }}aBaB{\boldsymbol {abc}}cc\\&{\underset {3}{\Rightarrow }}a{\boldsymbol {aB}}Babccc{\underset {3}{\Rightarrow }}aaB{\boldsymbol {aB}}bccc{\underset {3}{\Rightarrow }}aa{\boldsymbol {aB}}Bbccc\\&{\underset {4}{\Rightarrow }}aaaB{\boldsymbol {bb}}ccc{\underset {4}{\Rightarrow }}aaa{\boldsymbol {bb}}bccc\end{aligned}}}$

(En la notación: se lee "La cadena P genera la cadena Q mediante la producción i ", y la parte generada se indica cada vez en negrita.) ${\displaystyle P{\underset {i}{\Rightarrow }}Q}$

La jerarquía de Chomsky

Cuando Noam Chomsky formalizó por primera vez las gramáticas generativas en 1956, ^[2] las clasificó en tipos ahora conocidos como la jerarquía de Chomsky . La diferencia entre estos tipos es que tienen reglas de producción cada vez más estrictas y, por lo tanto, pueden expresar menos lenguajes formales. Dos tipos importantes son las gramáticas libres de contexto (Tipo 2) y las gramáticas regulares (Tipo 3). Los lenguajes que se pueden describir con una gramática de este tipo se denominan lenguajes libres de contexto y lenguajes regulares , respectivamente. Aunque mucho menos potentes que las gramáticas sin restricciones (Tipo 0), que de hecho pueden expresar cualquier lenguaje que pueda ser aceptado por una máquina de Turing , estos dos tipos restringidos de gramáticas se utilizan con mayor frecuencia porque los analizadores sintácticos para ellos se pueden implementar de manera eficiente. ^[7] Por ejemplo, todos los lenguajes regulares pueden ser reconocidos por una máquina de estados finitos , y para subconjuntos útiles de gramáticas libres de contexto existen algoritmos bien conocidos para generar analizadores sintácticos LL eficientes y analizadores sintácticos LR para reconocer los lenguajes correspondientes que generan esas gramáticas.

Gramáticas libres de contexto

Una gramática libre de contexto es una gramática en la que el lado izquierdo de cada regla de producción consta de un solo símbolo no terminal. Esta restricción no es trivial; no todos los idiomas pueden generarse mediante gramáticas libres de contexto. Aquellos que sí pueden hacerlo se denominan idiomas libres de contexto .

El lenguaje definido arriba no es un lenguaje libre de contexto, y esto se puede demostrar estrictamente usando el lema de bombeo para lenguajes libres de contexto , pero por ejemplo el lenguaje (al menos 1 seguido por el mismo número de 's) es libre de contexto, como se puede definir por la gramática con , , el símbolo de inicio, y las siguientes reglas de producción: ${\displaystyle L(G)=\left\{a^{n}b^{n}c^{n}\mid n\geq 1\right\}}$ ${\displaystyle \left\{a^{n}b^{n}\mid n\geq 1\right\}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G_{2}}$ ${\displaystyle N=\left\{S\right\}}$ ${\displaystyle \Sigma =\left\{a,b\right\}}$ ${\displaystyle S}$

1. ${\displaystyle S\rightarrow aSb}$

2. ${\displaystyle S\rightarrow ab}$

Un lenguaje libre de contexto puede ser reconocido en el tiempo ( ver notación Big O ) por un algoritmo como el reconocedor de Earley . Es decir, para cada lenguaje libre de contexto, se puede construir una máquina que tome una cadena como entrada y determine en el tiempo si la cadena es un miembro del lenguaje, donde es la longitud de la cadena. ^[8] Los lenguajes libres de contexto deterministas son un subconjunto de lenguajes libres de contexto que pueden reconocerse en tiempo lineal. ^[9] Existen varios algoritmos que apuntan a este conjunto de lenguajes o a algún subconjunto del mismo. ${\displaystyle O(n^{3})}$ ${\displaystyle O(n^{3})}$ ${\displaystyle n}$

Gramáticas regulares

En las gramáticas regulares , el lado izquierdo es nuevamente un solo símbolo no terminal, pero ahora el lado derecho también está restringido. El lado derecho puede ser la cadena vacía, o un solo símbolo terminal, o un solo símbolo terminal seguido de un símbolo no terminal, pero nada más. (A veces se utiliza una definición más amplia: se pueden permitir cadenas más largas de terminales o no terminales individuales sin nada más, lo que hace que los idiomas sean más fáciles de denotar mientras se sigue definiendo la misma clase de idiomas).

El lenguaje definido arriba no es regular, pero el lenguaje (al menos 1 seguido de al menos 1 , donde los números pueden ser diferentes) sí lo es, como puede definirse mediante la gramática con , , el símbolo de inicio, y las siguientes reglas de producción: ${\displaystyle \left\{a^{n}b^{n}\mid n\geq 1\right\}}$ ${\displaystyle \left\{a^{n}b^{m}\mid m,n\geq 1\right\}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle G_{3}}$ ${\displaystyle N=\left\{S,A,B\right\}}$ ${\displaystyle \Sigma =\left\{a,b\right\}}$ ${\displaystyle S}$

1. ${\displaystyle S\rightarrow aA}$
2. ${\displaystyle A\rightarrow aA}$
3. ${\displaystyle A\rightarrow bB}$
4. ${\displaystyle B\rightarrow bB}$
5. ${\displaystyle B\rightarrow \epsilon }$

Todos los lenguajes generados por una gramática regular pueden ser reconocidos en el tiempo por una máquina de estados finitos. Aunque en la práctica, las gramáticas regulares se expresan comúnmente mediante expresiones regulares , algunas formas de expresión regular utilizadas en la práctica no generan estrictamente los lenguajes regulares y no muestran un rendimiento de reconocimiento lineal debido a esas desviaciones. ${\displaystyle O(n)}$

Otras formas de gramáticas generativas

Los lingüistas y los informáticos han desarrollado numerosas extensiones y variaciones de la jerarquía original de gramáticas formales de Chomsky, normalmente para aumentar su poder expresivo o para que sean más fáciles de analizar o analizar sintácticamente. Algunas formas de gramática desarrolladas son:

• Las gramáticas contiguas a árboles aumentan la expresividad de las gramáticas generativas convencionales al permitir que las reglas de reescritura operen en árboles de análisis en lugar de solo en cadenas. ^[10]
• Las gramáticas de afijos ^[11] y las gramáticas de atributos ^{[12] [13]} permiten ampliar las reglas de reescritura con atributos y operaciones semánticas, útiles tanto para aumentar la expresividad gramatical como para construir herramientas prácticas de traducción del lenguaje.

Gramáticas recursivas

Una gramática recursiva es una gramática que contiene reglas de producción que son recursivas . Por ejemplo, una gramática para un lenguaje libre de contexto es recursiva por la izquierda si existe un símbolo no terminal A que se puede pasar a través de las reglas de producción para producir una cadena con A como el símbolo más a la izquierda. ^[14] Un ejemplo de gramática recursiva es una cláusula dentro de una oración separada por dos comas. ^[15] Todos los tipos de gramáticas en la jerarquía de Chomsky pueden ser recursivos.

Gramáticas analíticas

Aunque existe una gran cantidad de literatura sobre algoritmos de análisis sintáctico , la mayoría de estos algoritmos suponen que el lenguaje que se va a analizar se describe inicialmente mediante una gramática formal generativa y que el objetivo es transformar esta gramática generativa en un analizador funcional. Estrictamente hablando, una gramática generativa no se corresponde de ninguna manera con el algoritmo utilizado para analizar un lenguaje, y varios algoritmos tienen diferentes restricciones sobre la forma de las reglas de producción que se consideran bien formadas.

Un enfoque alternativo consiste en formalizar el lenguaje en términos de una gramática analítica en primer lugar, lo que corresponde más directamente a la estructura y la semántica de un analizador sintáctico para el lenguaje. Algunos ejemplos de formalismos de gramática analítica son los siguientes:

• Lenguaje de análisis de arriba hacia abajo (TDPL): un formalismo gramatical analítico altamente minimalista desarrollado a principios de la década de 1970 para estudiar el comportamiento de los analizadores de arriba hacia abajo . ^[16]
• Gramáticas de enlace : una forma de gramática analítica diseñada para la lingüística , que deriva la estructura sintáctica examinando las relaciones posicionales entre pares de palabras. ^{[17] [18]}
• Gramáticas de expresión de análisis (PEG): una generalización más reciente de TDPL diseñada en torno a las necesidades prácticas de expresividad de los escritores de lenguajes de programación y compiladores . ^[19]

Véase también

• Árbol de sintaxis abstracta
• Gramática adaptativa
• Gramática ambigua
• Forma Backus-Naur (BNF)
• Gramática categorial
• Árbol de sintaxis concreta
• Forma extendida de Backus-Naur (EBNF)
• Gramática
• Marco gramatical
• Sistema L
• Lojban
• Sistema postcanónico
• Gramática de formas
• Fórmula bien formada

Referencias

1. Meduna, Alexander (2014), Lenguajes formales y computación: modelos y sus aplicaciones, CRC Press, pág. 233, ISBN 9781466513457. Para más información sobre este tema, véase problema indecidible .
2. Chomsky, Noam (septiembre de 1956). "Tres modelos para la descripción del lenguaje". IRE Transactions on Information Theory . 2 (3): 113–124. doi :10.1109/TIT.1956.1056813. S2CID  19519474.
3. Chomsky, Noam (1957). Estructuras sintácticas . La Haya: Mouton .
4. Ginsburg, Seymour (1975). Propiedades teóricas algebraicas y de autómatas de los lenguajes formales . Holanda Septentrional. pp. 8-9. ISBN 978-0-7204-2506-2.
5. Harrison, Michael A. (1978). Introducción a la teoría formal del lenguaje . Reading, Mass.: Addison-Wesley Publishing Company. pág. 13. ISBN 978-0-201-02955-0.
6. Formas oracionales Archivado el 13 de noviembre de 2019 en Wayback Machine , Gramáticas libres de contexto, David Matuszek
7. Grune, Dick y Jacobs, Ceriel H., Técnicas de análisis sintáctico: una guía práctica , Ellis Horwood, Inglaterra, 1990.
8. Earley, Jay, "Un algoritmo de análisis sintáctico libre de contexto eficiente Archivado el 19 de mayo de 2020 en Wayback Machine " , Communications of the ACM , vol. 13, n.º 2, págs. 94-102, febrero de 1970.
9. Knuth, DE (julio de 1965). "Sobre la traducción de lenguas de izquierda a derecha". Información y control . 8 (6): 607–639. doi :10.1016/S0019-9958(65)90426-2.
10. Joshi, Aravind K., et al. , "Gramáticas adjuntas de árboles", Journal of Computer Systems Science , vol. 10, n.º 1, págs. 136-163, 1975.
11. Koster, Cornelis HA, "Gramáticas de afijos", en Implementación de ALGOL 68 , North Holland Publishing Company, Ámsterdam, págs. 95-109, 1971.
12. Knuth, Donald E., "Semántica de lenguajes libres de contexto", Mathematical Systems Theory , Vol. 2 No. 2, págs. 127-145, 1968.
13. Knuth, Donald E., "Semántica de lenguajes libres de contexto (corrección)", Mathematical Systems Theory , Vol. 5 No. 1, págs. 95-96, 1971.
14. Notas sobre teoría y análisis del lenguaje formal Archivado el 28 de agosto de 2017 en Wayback Machine , James Power, Departamento de Ciencias de la Computación, Universidad Nacional de Irlanda, Maynooth Maynooth, Co. Kildare, Irlanda.JPR02
15. Borenstein, Seth (27 de abril de 2006). "Los pájaros cantores también comprenden la gramática". Northwest Herald . p. 2 – vía Newspapers.com.
16. Birman, Alexander, The TMG Recognition Schema , Tesis doctoral, Universidad de Princeton, Departamento de Ingeniería Eléctrica, febrero de 1970.
17. Sleator, Daniel D. y Temperly, Davy, "Análisis del inglés con una gramática de enlaces", Informe técnico CMU-CS-91-196, Carnegie Mellon University Computer Science, 1991.
18. Sleator, Daniel D. y Temperly, Davy, "Análisis del inglés con una gramática de enlaces", Tercer taller internacional sobre tecnologías de análisis , 1993. (Versión revisada del informe anterior).
19. Ford, Bryan, Packrat Parsing: a Practical Linear-Time Algorithm with Backtracking , tesis de maestría, Instituto Tecnológico de Massachusetts, septiembre de 2002.

Enlaces externos