Esquema de elevación

Técnica para el análisis wavelet

Secuencia de elevación que consta de dos pasos

El esquema de elevación es una técnica tanto para diseñar wavelets como para realizar la transformada wavelet discreta (DWT). En una implementación, a menudo vale la pena fusionar estos pasos y diseñar los filtros wavelet mientras se realiza la transformada wavelet. Esto se denomina transformada wavelet de segunda generación . La técnica fue introducida por Wim Sweldens . ^[1]

El esquema de elevación factoriza cualquier transformada wavelet discreta con filtros finitos en una serie de operadores de convolución elementales, denominados pasos de elevación, lo que reduce el número de operaciones aritméticas en casi un factor de dos. El tratamiento de los límites de la señal también se simplifica. ^[2]

La transformada wavelet discreta aplica varios filtros por separado a la misma señal. En cambio, en el esquema de elevación, la señal se divide como una cremallera y luego se aplica una serie de operaciones de convolución y acumulación en las señales divididas.

Lo esencial

La versión más simple de una transformada wavelet hacia adelante expresada en el esquema de elevación se muestra en la figura anterior. significa paso de predicción, que se considerará de forma aislada. El paso de predicción calcula la función wavelet en la transformada wavelet. Este es un filtro de paso alto. El paso de actualización calcula la función de escala, que da como resultado una versión más suave de los datos. ${\displaystyle P}$

Como se mencionó anteriormente, el esquema de elevación es una técnica alternativa para realizar la DWT utilizando wavelets biortogonales. Para realizar la DWT utilizando el esquema de elevación, los pasos de elevación y escala correspondientes deben derivarse de los wavelets biortogonales. Los filtros de análisis ( ) del wavelet en particular se escriben primero en la matriz polifásica ${\displaystyle g,h}$

${\displaystyle P(z)={\begin{bmatrix}h_{\text{even}}(z)&g_{\text{even}}(z)\\h_{\text{odd}}(z)&g_{\text{odd}}(z)\end{bmatrix}},}$

dónde . ${\displaystyle \det P(z)=z^{-m}}$

La matriz polifásica es una matriz de 2 × 2 que contiene los filtros de paso bajo y paso alto de análisis, cada uno dividido en sus coeficientes polinómicos pares e impares y normalizado. A partir de aquí, la matriz se factoriza en una serie de matrices triangulares superior e inferior de 2 × 2, cada una con entradas diagonales iguales a 1. Las matrices triangulares superiores contienen los coeficientes para los pasos de predicción y las matrices triangulares inferiores contienen los coeficientes para los pasos de actualización. Se puede extraer una matriz que consta de todos los ceros con la excepción de los valores diagonales para derivar los coeficientes de los pasos de escala. La matriz polifásica se factoriza en la forma

${\displaystyle P(z)={\begin{bmatrix}1&a(1+z^{-1})\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\b(1+z)&1\end{bmatrix}},}$

donde es el coeficiente para el paso de predicción y es el coeficiente para el paso de actualización. ${\displaystyle a}$ ${\displaystyle b}$

A continuación se muestra un ejemplo de una extracción más complicada que tiene múltiples pasos de predicción y actualización, así como pasos de escala; es el coeficiente para el primer paso de predicción, es el coeficiente para el primer paso de actualización, es el coeficiente para el segundo paso de predicción, es el coeficiente para el segundo paso de actualización, es el coeficiente de escala de muestra impar, y es el coeficiente de escala de muestra par: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle k_{1}}$ ${\displaystyle k_{2}}$

${\displaystyle P(z)={\begin{bmatrix}1&a(1+z^{-1})\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\b(1+z)&1\end{bmatrix}}{\begin{bmatrix}1&c(1+z^{-1})\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\d(1+z)&1\end{bmatrix}}{\begin{bmatrix}k_{1}&0\\0&k_{2}\end{bmatrix}}.}$

Según la teoría de matrices, cualquier matriz que tenga entradas polinómicas y un determinante de 1 se puede factorizar como se describió anteriormente. Por lo tanto, cada transformada wavelet con filtros finitos se puede descomponer en una serie de pasos de elevación y escalado. Daubechies y Sweldens analizan la extracción por pasos de elevación con más detalle. ^[3]

Filtro CDF 9/7

Para realizar la transformación CDF 9/7, se requieren cuatro pasos de elevación en total: dos de predicción y dos de actualización. La factorización de elevación conduce a la siguiente secuencia de pasos de filtrado. ^[3]

${\displaystyle d_{l}=d_{l}+a(s_{l}+s_{l+1}),}$

${\displaystyle s_{l}=s_{l}+b(d_{l}+d_{l-1}),}$

${\displaystyle d_{l}=d_{l}+c(s_{l}+s_{l+1}),}$

${\displaystyle s_{l}=s_{l}+d(d_{l}+d_{l-1}),}$

${\displaystyle d_{l}=k_{1}d_{l},}$

${\displaystyle s_{l}=k_{2}s_{l}.}$

Propiedades

Reconstrucción perfecta

Cada transformación realizada por el esquema de elevación se puede invertir. Cada banco de filtros de reconstrucción perfecta se puede descomponer en pasos de elevación mediante el algoritmo euclidiano . Es decir, "banco de filtros descomponible por elevación" y "banco de filtros de reconstrucción perfecta" denotan lo mismo. Cada dos bancos de filtros de reconstrucción perfecta se pueden transformar entre sí mediante una secuencia de pasos de elevación. Para una mejor comprensión, si y son matrices polifásicas con el mismo determinante, entonces la secuencia de elevación de a es la misma que la de la matriz polifásica perezosa a . ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle I}$ ${\displaystyle P^{-1}\cdot Q}$

Aceleración

La aceleración se duplica. Esto solo es posible porque la elevación está restringida a los bancos de filtros de reconstrucción perfecta. Es decir, la elevación, de alguna manera, elimina las redundancias causadas por la reconstrucción perfecta.

La transformación se puede realizar inmediatamente en la memoria de los datos de entrada (en el lugar, in situ) con solo una sobrecarga de memoria constante.

No linealidades

Las operaciones de convolución pueden reemplazarse por cualquier otra operación. Para una reconstrucción perfecta, solo es relevante la invertibilidad de la operación de adición. De esta manera, se pueden tolerar errores de redondeo en la convolución y es posible la reconstrucción con precisión de bits. Sin embargo, la estabilidad numérica puede verse reducida por las no linealidades. Esto debe respetarse si la señal transformada se procesa como en la compresión con pérdida . Aunque cada banco de filtros reconstruible puede expresarse en términos de pasos de elevación, una descripción general de los pasos de elevación no es obvia a partir de una descripción de una familia de ondículas. Sin embargo, por ejemplo, para casos simples de la ondícula de Cohen–Daubechies–Feauveau , existe una fórmula explícita para sus pasos de elevación.

Aumento de los momentos de desaparición, estabilidad y regularidad.

Un levantamiento modifica los filtros biortogonales para aumentar el número de momentos de desaparición de las ondículas biortogonales resultantes y, con suerte, su estabilidad y regularidad. Aumentar el número de momentos de desaparición disminuye la amplitud de los coeficientes de ondículas en regiones donde la señal es regular, lo que produce una representación más dispersa. Sin embargo, aumentar el número de momentos de desaparición con un levantamiento también aumenta el soporte de ondículas, que es un efecto adverso que aumenta el número de coeficientes grandes producidos por singularidades aisladas. Cada paso de levantamiento mantiene la biortogonalidad del filtro pero no proporciona control sobre los límites de Riesz y, por lo tanto, sobre la estabilidad de la base biortogonal de ondículas resultante. Cuando una base es ortogonal, la base dual es igual a la base original. Tener una base dual que sea similar a la base original es, por lo tanto, una indicación de estabilidad. Como resultado, la estabilidad generalmente mejora cuando las ondículas duales tienen tantos momentos de desaparición como las ondículas originales y un soporte de tamaño similar. Esta es la razón por la que un procedimiento de levantamiento también aumenta el número de momentos de desaparición de las ondículas duales. También puede mejorar la regularidad de la ondícula dual. Se calcula un diseño de elevación ajustando el número de momentos de desaparición. La estabilidad y regularidad de las ondículas biortogonales resultantes se miden a posteriori, esperando que se obtenga el mejor resultado. Esta es la principal debilidad de este procedimiento de diseño de ondículas.

Levantamiento generalizado

Diagrama de bloques del esquema de transformación de elevación (hacia adelante)

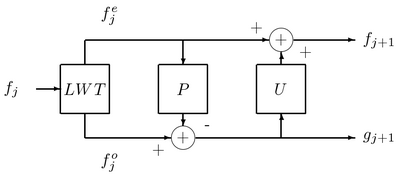
El esquema de elevación generalizado fue desarrollado por Joel Solé y Philippe Salembier y publicado en la tesis doctoral de Solé. ^[4] Se basa en el esquema de elevación clásico y lo generaliza eliminando una restricción oculta en la estructura del esquema. El esquema de elevación clásico tiene tres tipos de operaciones:

1. Una transformada wavelet perezosa divide la señal en dos nuevas señales: la señal de muestras impares denotada por y la señal de muestras pares denotada por . ${\displaystyle f_{j}[n]}$ ${\displaystyle f_{j}^{o}[n]}$ ${\displaystyle f_{j}^{e}[n]}$
2. Un paso de predicción calcula una predicción para las muestras impares, en función de las muestras pares (o viceversa). Esta predicción se resta de las muestras impares, lo que crea una señal de error . ${\displaystyle g_{j+1}[n]}$
3. Un paso de actualización recalibra la rama de baja frecuencia con parte de la energía eliminada durante el submuestreo. En el caso del levantamiento clásico, esto se utiliza para "preparar" la señal para el siguiente paso de predicción. Utiliza las muestras impares predichas para preparar las pares (o viceversa). Esta actualización se resta de las muestras pares, lo que produce la señal denotada por . ${\displaystyle g_{j+1}[n]}$ ${\displaystyle f_{j}^{e}[n]}$ ${\displaystyle f_{j+1}[n]}$

El esquema es invertible debido a su estructura. En el receptor , el paso de actualización se calcula primero con su resultado agregado nuevamente a las muestras pares, y luego es posible calcular exactamente la misma predicción para agregarla a las muestras impares. Para recuperar la señal original, la transformada wavelet perezosa debe invertirse. El esquema de elevación generalizado tiene los mismos tres tipos de operaciones. Sin embargo, este esquema evita la restricción de adición-sustracción que ofrecía la elevación clásica, lo que tiene algunas consecuencias. Por ejemplo, el diseño de todos los pasos debe garantizar la invertibilidad del esquema (no se garantiza si se evita la restricción de adición-sustracción).

Definición

Diagrama de bloques de la transformación del esquema de elevación generalizado (hacia adelante)

El esquema de elevación generalizado es una transformación diádica que sigue estas reglas:

1. Desentrelaza la entrada en un flujo de muestras pares y otro flujo de muestras impares. A esto a veces se lo denomina transformada wavelet perezosa .
2. Calcula una correlación de predicción . Este paso intenta predecir las muestras impares teniendo en cuenta las pares (o viceversa). Existe una correlación desde el espacio de las muestras en al espacio de las muestras en . En este caso, las muestras (de ) elegidas como referencia para se denominan contexto . Se podría expresar como ${\displaystyle f_{j}^{e}[n]}$ ${\displaystyle g_{j+1}[n]}$ ${\displaystyle f_{j}^{e}[n]}$ ${\displaystyle f_{j}^{o}[n]}$

   ${\displaystyle g_{j+1}[n]=P(f_{j}^{o}[n];f_{j}^{e}[n]).}$

3. Calcula un mapeo de actualización . Este paso intenta actualizar las muestras pares teniendo en cuenta las muestras impares predichas. Sería una especie de preparación para el siguiente paso de predicción, si lo hubiera. Podría expresarse como

   ${\displaystyle f_{j+1}[n]=U(f_{j}^{e}[n];g_{j+1}[n]).}$

Obviamente, estas asignaciones no pueden ser funciones cualesquiera. Para garantizar la invertibilidad del esquema en sí, todas las asignaciones involucradas en la transformación deben ser invertibles. En caso de que surjan asignaciones y lleguen a conjuntos finitos (señales de valores discretos acotados), esta condición es equivalente a decir que las asignaciones son inyectivas (uno a uno). Además, si una asignación va de un conjunto a un conjunto de la misma cardinalidad, debe ser biyectiva .

En el esquema de elevación generalizado, la restricción de adición/sustracción se evita al incluir este paso en el mapeo. De esta manera, se generaliza el esquema de elevación clásico.

Diseño

Se han desarrollado algunos diseños para el mapeo de pasos de predicción. El diseño de pasos de actualización no se ha considerado tan a fondo, porque aún queda por responder cómo exactamente es útil el paso de actualización. La principal aplicación de esta técnica es la compresión de imágenes. Hay algunas referencias interesantes como, ^{[5] [6] [7]} y. ^[8]

Aplicaciones

• Transformadas wavelet que asignan números enteros a números enteros
• Transformada de Fourier con reconstrucción de bits exactos ^[9]
• Construcción de wavelets con un número requerido de factores de suavidad y momentos de desaparición
• Construcción de wavelets adaptados a un patrón determinado ^[10]
• Implementación de la transformada wavelet discreta en JPEG 2000
• Transformaciones basadas en datos, por ejemplo, wavelets que evitan los bordes ^[11]
• Transformadas wavelet en redes no separables , por ejemplo, wavelets rojo-negro en la red quincuncial ^[12]

Véase también

• El esquema Feistel en criptología utiliza en gran medida la misma idea de dividir datos y alternar la aplicación de funciones con la suma. Tanto en el esquema Feistel como en el esquema de elevación, esto se utiliza para la encodificación y decodificación simétricas.

Referencias

1. Sweldens, Wim (1997). "El esquema de elevación: una construcción de wavelets de segunda generación" (PDF) . Revista de análisis matemático . 29 (2): 511–546. doi :10.1137/S0036141095289051.
2. Mallat, Stéphane (2009). Un recorrido wavelet por el procesamiento de señales. Academic Press. ISBN 978-0-12-374370-1.
3. Daubechies, Ingrid ; Sweldens, Wim (1998). "Factorización de transformadas wavelet en pasos de elevación" (PDF) . Revista de análisis y aplicaciones de Fourier . 4 (3): 247–269. doi :10.1007/BF02476026.
4. Tesis doctoral: Optimización y generalización de esquemas de elevación: aplicación a la compresión de imágenes sin pérdida .
5. Rolon, JC; Salembier, P. (7–9 de noviembre de 2007). "Levantamiento generalizado para la representación y codificación de imágenes dispersas". Simposio de codificación de imágenes, PCS 2007 .
6. Rolón, Julio C.; Salembier, Philippe; Alameda-Pineda, Xavier (2008). "Compresión de imágenes con Generalized Lifting y conocimiento parcial de la señal pdf" (PDF) . Actas de la Conferencia Internacional sobre Procesamiento de Imágenes, ICIP 2008, 12-15 de octubre de 2008, San Diego, California, EE. UU . . IEEE. pp. 129-132. doi :10.1109/ICIP.2008.4711708. ISBN 978-1-4244-1765-0.
7. Rolon, JC; Ortega, A.; Salembier, P. "Modelado de contornos en el dominio wavelet para compresión de imágenes de elevación generalizada" (PDF) . ICASSP 2009 (enviado) .
8. Rolon, JC; Mendonça, E.; Salembier, P. Levantamiento generalizado con estimación local adaptativa en PDF para codificación de imágenes (PDF) .
9. Oraintara, Soontorn; Chen, Ying-Jui; Nguyen, Truong Q. (2002). "Transformada rápida de Fourier entera" (PDF) . IEEE Transactions on Signal Processing . 50 (3): 607–618. Bibcode :2002ITSP...50..607O. doi :10.1109/78.984749.
10. Thielemann, Henning (2004). "Ondículas óptimamente emparejadas". Actas en Matemáticas Aplicadas y Mecánica . 4 : 586–587. doi : 10.1002/pamm.200410274 .
11. Fattal, Raanan (2009). "Widlets que evitan los bordes y sus aplicaciones". ACM Transactions on Graphics . 28 (3): 1–10. CiteSeerX 10.1.1.205.8462 . doi :10.1145/1531326.1531328. 
12. Uytterhoeven, Geert; Bultheel, Adhemar (1998). La transformada wavelet roja-negra. Simposio de procesamiento de señales (IEEE Benelux). págs. 191-194.

Enlaces externos

• Esquema de elevación: breve descripción del algoritmo de factorización
• Introducción al esquema de elevación
• La transformada wavelet de elevación rápida