espiral de euler

Curva cuya curvatura cambia linealmente.

Una espiral de Euler de doble extremo. La curva continúa convergiendo hacia los puntos marcados, ya que t tiende al infinito positivo o negativo.

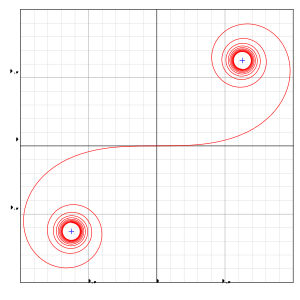
Una espiral de Euler es una curva cuya curvatura cambia linealmente con la longitud de la curva (la curvatura de una curva circular es igual al recíproco del radio). Esta curva también se conoce como clotoide o espiral de Cornu . ^{[1] [2]} El comportamiento de las integrales de Fresnel se puede ilustrar mediante una espiral de Euler, una conexión realizada por primera vez por Alfred Marie Cornu en 1874. ^[3] La espiral de Euler es un tipo de superespiral que tiene la propiedad de una función de curvatura monótona. ^[4]

La espiral de Euler tiene aplicaciones en los cálculos de difracción . También se utilizan ampliamente en ingeniería ferroviaria y de carreteras para diseñar curvas de transición entre tramos rectos y curvos de vías férreas o carreteras. También se encuentra una aplicación similar en los circuitos integrados fotónicos . El principio de variación lineal de la curvatura de la curva de transición entre una tangente y una curva circular define la geometría de la espiral de Euler:

• Su curvatura comienza en cero en la sección recta (la tangente) y aumenta linealmente con la longitud de la curva.
• Donde la espiral de Euler se encuentra con la curva circular, su curvatura se vuelve igual a la de esta última.

Historia

La espiral tiene múltiples nombres que reflejan su descubrimiento y aplicación en múltiples campos. Los tres ámbitos principales fueron los resortes elásticos ("espiral de Euler", 1744), los cálculos gráficos en difracción de la luz ("espiral de Cornu", 1874) y las transiciones ferroviarias ("la espiral de transición ferroviaria", 1890). ^[2]

El trabajo de Leonhard Euler sobre la espiral se produjo después de que James Bernoulli planteara un problema en la teoría de la elasticidad: ¿qué forma debe tener un resorte de alambre precurvado de modo que, cuando se aplana presionando el extremo libre, se convierta en una línea recta? Euler estableció las propiedades de la espiral en 1744, señalando en ese momento que la curva debe tener dos límites, puntos que la curva gira una y otra vez pero que nunca alcanza. Treinta y ocho años después, en 1781, informó de su descubrimiento de la fórmula del límite (por "feliz casualidad"). ^[2]

Augustin Fresnel , trabajando en 1818 sobre la difracción de la luz, desarrolló la integral de Fresnel que define la misma espiral. No conocía las integrales de Euler ni la conexión con la teoría de la elasticidad. En 1874, Alfred Marie Cornu demostró que la intensidad de la difracción se podía leer en una gráfica de la espiral elevando al cuadrado la distancia entre dos puntos de la gráfica. En su reseña biográfica de Cornu, Henri Poincaré elogió las ventajas de la "espiral de Cornu" sobre la "desagradable multitud de fórmulas integrales peludas". Ernesto Cesaro optó por llamar a la misma curva "clotoide" en honor a Cloto , una de las tres Parcas que hilan el hilo de la vida en la mitología griega. ^[2]

El tercer descubrimiento independiente se produjo en el siglo XIX, cuando varios ingenieros ferroviarios buscaron una fórmula para la curvatura gradual de la forma de las vías. En 1880, Arthur Newell Talbot desarrolló las fórmulas integrales y su solución, a las que llamó "espiral de transición ferroviaria". La conexión con la obra de Euler no se estableció hasta 1922. ^[2]

Aplicaciones

Curva de transición de vía

Animación que muestra la evolución de una espiral de Cornu con el círculo tangencial con el mismo radio de curvatura que en su punta, también conocido como círculo osculador .

Para viajar a lo largo de una trayectoria circular, un objeto necesita estar sujeto a una aceleración centrípeta (por ejemplo: la Luna gira alrededor de la Tierra debido a la gravedad; un automóvil gira sus ruedas delanteras hacia adentro para generar una fuerza centrípeta). Si un vehículo que viaja en una trayectoria recta hiciera una transición repentina a una trayectoria circular tangencial, requeriría una aceleración centrípeta que cambiara repentinamente en el punto tangente de cero al valor requerido; Esto sería difícil de lograr (piense en un conductor que mueve instantáneamente el volante de la línea recta a la posición de giro, y el automóvil realmente lo hace), lo que ejercería tensión mecánica sobre las partes del vehículo y causaría mucha incomodidad (debido al tirón lateral ).

En los primeros ferrocarriles, esta aplicación instantánea de fuerza lateral no era un problema ya que se empleaban velocidades bajas y curvas de radio amplio (las fuerzas laterales sobre los pasajeros y el balanceo lateral eran pequeños y tolerables). A medida que las velocidades de los vehículos ferroviarios aumentaron a lo largo de los años, se hizo evidente que era necesaria una servidumbre para que la aceleración centrípeta aumentara suavemente con la distancia recorrida. Dada la expresión de la aceleración centrípeta.v ²/r, la solución obvia es proporcionar una curva de servidumbre cuya curvatura,1/R, aumenta linealmente con la distancia recorrida. Esta geometría es una "clotoide", otro nombre de la espiral de Euler. ^[5]

Desconociendo la solución de la geometría de Leonhard Euler , Rankine citó la curva cúbica (una curva polinómica de grado 3), que es una aproximación de la espiral de Euler para pequeños cambios angulares del mismo modo que una parábola es una aproximación a una circular. curva.

Marie Alfred Cornu (y más tarde algunos ingenieros civiles) también resolvieron el cálculo de la espiral de Euler de forma independiente. Las espirales de Euler se utilizan ahora ampliamente en la ingeniería ferroviaria y de carreteras para proporcionar una transición o servidumbre entre una curva circular tangente y horizontal.

Óptica

En óptica se utiliza el término "espiral de Cornu". ^{[6] : 432} La espiral de Cornu se puede utilizar para describir un patrón de difracción . ^[7] Considere una onda plana con amplitud fasorial E ₀ e ^{− jkz} que se difracta por un "filo de cuchillo" de altura h por encima de x = 0 en el plano z = 0 . Entonces el campo de onda difractada se puede expresar como

$${\displaystyle \mathbf {E} (x,z)=E_{0}e^{-jkz}{\frac {\mathrm {Fr} (\infty )-\mathrm {Fr} \left({\sqrt {\frac {2}{\lambda z}}}(h-x)\right)}{\mathrm {Fr} (\infty )-\mathrm {Fr} (-\infty )}},}$$

Fr( x )

Entonces, para simplificar el cálculo de la atenuación de la onda plana cuando se difracta del filo de la navaja, se puede usar el diagrama de una espiral de Cornu representando las cantidades Fr( a ) − Fr( b ) como las distancias físicas entre los puntos representados. por Fr( a ) y Fr( b ) para a y b apropiados . Esto facilita un cálculo aproximado de la atenuación de la onda plana por el filo de altura h en una ubicación ( x , z ) más allá del filo.

Óptica integrada

Las curvaturas con radio de curvatura que varía continuamente siguiendo la espiral de Euler también se utilizan para reducir las pérdidas en circuitos integrados fotónicos , ya sea en guías de onda monomodo , ^{[8] [9]} para suavizar el cambio abrupto de curvatura y suprimir el acoplamiento a modos de radiación, o en multimodo. guías de onda, ^[10] para suprimir el acoplamiento a modos de orden superior y garantizar un funcionamiento monomodo eficaz. Ya en 1957 se realizó una aplicación pionera y muy elegante de la espiral de Euler a guías de ondas, ^[11] con una guía de ondas metálica hueca para microondas. Allí, la idea era explotar el hecho de que una guía de ondas de metal recta se puede doblar físicamente para adoptar de forma natural una forma de curvatura gradual que se asemeje a una espiral de Euler.

Integral del camino de Feynman

En la formulación integral de trayectoria de la mecánica cuántica, la amplitud de probabilidad de propagación entre dos puntos se puede visualizar conectando flechas de fase de acción para cada paso de tiempo entre los dos puntos. Las flechas giran alrededor de cada punto final formando lo que se denomina espiral de Cornu. ^[12]

Carrera de autos

El autor de deportes de motor Adam Brouillard ha mostrado el uso de la espiral de Euler para optimizar la línea de carrera durante la parte de entrada a la curva. ^[13]

Tipografía y dibujo vectorial digital.

Raph Levien lanzó Spiro como un conjunto de herramientas para el diseño de curvas, especialmente el diseño de fuentes, en 2007 ^{[14] [15]} bajo una licencia gratuita. Este conjunto de herramientas se implementó bastante rápidamente en la herramienta de diseño de fuentes Fontforge y en el dibujo vectorial digital Inkscape .

Proyección de mapas

Cortar una esfera a lo largo de una espiral con ancho.1/nortey al aplanar la forma resultante se obtiene una espiral de Euler cuando n tiende al infinito. ^[16] Si la esfera es el globo , esto produce una proyección cartográfica cuya distorsión tiende a cero cuando n tiende al infinito. ^[17]

Formas de bigotes

Las formas naturales de los bigotes de las ratas se aproximan bien mediante segmentos de espirales de Euler; para una sola rata, todos los bigotes pueden aproximarse como segmentos de la misma espiral. ^[18] Los dos parámetros de la ecuación de Cesàro para un segmento de espiral de Euler podrían dar una idea del mecanismo de queratinización del crecimiento de los bigotes. ^[19]

Formulación

Símbolos

Expansión de la integral de Fresnel

Si a = 1 , que es el caso de la curva de Euler normalizada, entonces las coordenadas cartesianas vienen dadas por integrales de Fresnel (o integrales de Euler):

$${\displaystyle {\begin{aligned}C(L)&=\int _{0}^{L}\cos \left(s^{2}\right)\,ds\\S(L)&=\int _{0}^{L}\sin \left(s^{2}\right)\,ds\end{aligned}}}$$

Normalización

Para una curva de Euler dada con:

$${\displaystyle 2RL=2R_{c}L_{s}={\frac {1}{a^{2}}}}$$

$${\displaystyle {\frac {1}{R}}={\frac {L}{R_{c}L_{s}}}=2a^{2}L}$$

$${\displaystyle {\begin{aligned}x&={\frac {1}{a}}\int _{0}^{L'}\cos \left(s^{2}\right)\,ds\\y&={\frac {1}{a}}\int _{0}^{L'}\sin \left(s^{2}\right)\,ds\end{aligned}}}$$

$${\displaystyle {\begin{aligned}L'&=aL\\a&={\frac {1}{\sqrt {2R_{c}L_{s}}}}.\end{aligned}}}$$

El proceso de obtención de la solución de ( x , y ) de una espiral de Euler puede describirse así como:

• Mapee L de la espiral de Euler original multiplicando con el factor a a L ′ de la espiral de Euler normalizada;
• Encuentre ( x ′, y ′) a partir de las integrales de Fresnel; y
• Asigne ( x ′, y ′) a ( x , y ) ampliando (desnormalizando) con factor1/a. Tenga en cuenta que1/a> 1 .

En el proceso de normalización,

$${\displaystyle {\begin{aligned}R'_{c}&={\frac {R_{c}}{\sqrt {2R_{c}L_{s}}}}={\sqrt {\frac {R_{c}}{2L_{s}}}}\\L'_{s}&={\frac {L_{s}}{\sqrt {2R_{c}L_{s}}}}={\sqrt {\frac {L_{s}}{2R_{c}}}}\end{aligned}}}$$

$${\displaystyle 2R'_{c}L'_{s}=2{\sqrt {\frac {R_{c}}{2L_{s}}}}{\sqrt {\frac {L_{s}}{2R_{c}}}}={\frac {2}{2}}=1}$$

Generalmente, la normalización reduce L ′ a un valor pequeño (menos de 1) y da como resultado buenas características convergentes de la integral de Fresnel manejables con solo unos pocos términos (a un precio de mayor inestabilidad numérica del cálculo, especialmente para valores de θ más grandes ). .

Ilustración

Dado:

$${\displaystyle {\begin{aligned}R_{c}&=300\,\mathrm {m} \\L_{s}&=100\,\mathrm {m} \end{aligned}}}$$

$${\displaystyle \theta _{s}={\frac {L_{s}}{2R_{c}}}={\frac {100}{2\times 300}}={\frac {1}{6}}\ \mathrm {radian} }$$

$${\displaystyle 2R_{c}L_{s}=60\,000}$$

Reducimos la espiral de Euler en √60 000 , es decir 100√ 6 a la espiral de Euler normalizada que tiene:

$${\displaystyle {\begin{aligned}R'_{c}&={\tfrac {3}{\sqrt {6}}}\,\mathrm {m} \\L'_{s}&={\tfrac {1}{\sqrt {6}}}\,\mathrm {m} \\2R'_{c}L'_{s}&=2\times {\tfrac {3}{\sqrt {6}}}\times {\tfrac {1}{\sqrt {6}}}\\&=1\end{aligned}}}$$

$${\displaystyle \theta _{s}={\frac {L'_{s}}{2R'_{c}}}={\frac {\frac {1}{\sqrt {6}}}{2\times {\frac {3}{\sqrt {6}}}}}={\frac {1}{6}}\ \mathrm {radian} }$$

Los dos ángulos θ _s son iguales. Esto confirma así que las espirales de Euler originales y normalizadas son geométricamente similares. El lugar geométrico de la curva normalizada se puede determinar a partir de la integral de Fresnel, mientras que el lugar geométrico de la espiral de Euler original se puede obtener ampliando o desnormalizando.

Otras propiedades de las espirales de Euler normalizadas

Las espirales de Euler normalizadas se pueden expresar como:

$${\displaystyle {\begin{aligned}x&=\int _{0}^{L}\cos \left(s^{2}\right)\,ds\\y&=\int _{0}^{L}\sin \left(s^{2}\right)\,ds\end{aligned}}}$$

serie de potencias

$${\displaystyle {\begin{aligned}x&=\left.\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {s^{4i+1}}{4i+1}}\right|_{0}^{L}&&=\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {L^{4i+1}}{4i+1}}\\y&=\left.\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {s^{4i+3}}{4i+3}}\right|_{0}^{L}&&=\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {L^{4i+3}}{4i+3}}\end{aligned}}}$$

La espiral de Euler normalizada convergerá a un solo punto en el límite cuando el parámetro L se acerque al infinito, lo que se puede expresar como:

$${\displaystyle {\begin{aligned}x^{\prime }&=\lim _{L\to \infty }\int _{0}^{L}\cos \left(s^{2}\right)\,ds&&={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx 0.6267\\y^{\prime }&=\lim _{L\to \infty }\int _{0}^{L}\sin \left(s^{2}\right)\,ds&&={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx 0.6267\end{aligned}}}$$

Las espirales de Euler normalizadas tienen las siguientes propiedades:

$${\displaystyle {\begin{aligned}2R_{c}L_{s}&=1\\\theta _{s}&={\frac {L_{s}}{2R_{c}}}=L_{s}^{2}\end{aligned}}}$$

$${\displaystyle {\begin{aligned}\theta &=\theta _{s}\cdot {\frac {L^{2}}{L_{s}^{2}}}=L^{2}\\{\frac {1}{R}}&={\frac {d\theta }{dL}}=2L\end{aligned}}}$$

Tenga en cuenta que 2 R _c L _s = 1 también significa1/Rc_​= 2 L _s , de acuerdo con el último enunciado matemático.

Ver también

• Lista de espirales

Referencias

1. Von Seggern, David H. (1994). Manual práctico de diseño y generación de curvas . Boca Ratón, Florida: CRC Press. ISBN 978-0-8493-8916-0.
2. Levien, Raph. "La espiral de Euler: una historia matemática". Rap. tecnología (2008).
3. María Alfred Cornu. M´ethode nouvelle pour la discusión de los problemas de difracción en el caso de una onda cilíndrica. Journal de Physique th´eoretique et appliqu´ee, páginas 5–15, 1874.
4. Ziatdinov, R. (2012), "Familia de superespirales con curvatura completamente monótona dada en términos de función hipergeométrica de Gauss", Diseño geométrico asistido por computadora , 29 (7): 510–518
5. Constantino (7 de marzo de 2016). "La clotoide". Pwayblog . Consultado el 7 de junio de 2023 .
6. Nacido, Max; Lobo, Emil (1993). Principios de la óptica: teoría electromagnética de la propagación, interferencia y difracción de la luz (6. ed., reimpreso (con correcciones) ed.). Oxford: Prensa de Pérgamo. ISBN 978-0-08-026481-3.
7. Eugenio Hecht (1998). Óptica (3ª ed.). Addison-Wesley. pag. 491.ISBN​ 978-0-201-30425-1.
8. Kohtoku, M.; et al. (7 de julio de 2005). "Nuevas técnicas de fabricación de guías de ondas para PLC de próxima generación" (PDF) . Revisión técnica de NTT . 3 (7): 37–41 . Consultado el 24 de enero de 2017 .
9. Li, G.; et al. (11 de mayo de 2012). "Enrutamiento de guía de ondas ópticas SOI de alta densidad y pérdida ultrabaja para interconexiones de macrochips". Óptica Express . 20 (11): 12035–12039. Código Bib : 2012OExpr..2012035L. doi : 10.1364/OE.20.012035 . PMID  22714189.
10. Cherchi, M.; et al. (18 de julio de 2013). "Reducción espectacular del tamaño de las curvaturas de la guía de ondas en una plataforma fotónica de silicio a escala micrométrica". Óptica Express . 21 (15): 17814–17823. arXiv : 1301.2197 . Código Bib : 2013OExpr..2117814C. doi :10.1364/OE.21.017814. PMID  23938654.
11. Unger, HG (septiembre de 1957). "Curvas en modo normal para ondas eléctricas circulares". La revista técnica de Bell System . 36 (5): 1292-1307. doi :10.1002/j.1538-7305.1957.tb01509.x.
12. Taylor, Edwin F.; Vokos, Stamatis; O'Meara, John M.; Thornber, Nora S. (1 de marzo de 1998). "Enseñanza de la teoría cuántica de suma sobre caminos de Feynman". Computadoras en Física . 12 (2): 190–199. doi : 10.1063/1.168652 . ISSN  0894-1866.
13. Desarrollo, impulsor del cambio de paradigma; Brouillard, Adam (18 de marzo de 2016). La curva perfecta: una guía paso a paso para que el conductor encuentre su propia línea óptima a través de la física de las carreras . Libros de deportes de motor de cambio de paradigma. ISBN 9780997382426.
14. "Espiro".
15. "| Lanzamiento de Spiro 0.01 | Typophile". www.typophile.com . Archivado desde el original el 10 de mayo de 2007.
16. Bartholdi, Laurent; Henriques, André (2012). "Cáscaras de naranja e integrales de Fresnel". El inteligente matemático . 34 (3): 1–3. arXiv : 1202.3033 . doi :10.1007/s00283-012-9304-1. ISSN  0343-6993. S2CID  52592272.
17. "Una extraña proyección de mapa (espiral de Euler) - Numéfilo". YouTube . Archivado desde el original el 21 de diciembre de 2021.
18. Toalla, RB; et al. (7 de abril de 2011). "La morfología de la matriz vibrisal de rata: un modelo para cuantificar patrones espaciotemporales de contacto bigote-objeto". Biología Computacional PLoS . 7 (4): e1001120. doi : 10.1371/journal.pcbi.1001120 . PMC 3072363 . PMID  21490724. 
    Starostin, EL; et al. (15 de enero de 2020). "La espiral de Euler de bigotes de rata". Avances científicos . 6 (3): eax5145. Código Bib : 2020SciA....6.5145S. doi : 10.1126/sciadv.aax5145 . PMC  6962041 . PMID  31998835.
19. Luo, Y.; Hartmann, MJ (enero de 2023). "Sobre la curvatura intrínseca de los bigotes de los animales". Más uno . 18 (1): e0269210. doi : 10.1371/journal.pone.0269210 . PMC 9821693 . PMID  36607960. 

Otras lecturas

• Kellogg, Norman Benjamín (1907). La curva de transición o curva de ajuste (3ª ed.). Nueva York: McGraw.
• R. Nave, La espiral de Cornu, Hiperfísica (2002) (Utiliza πt²/2 en lugar de t².)
• Milton Abramowitz e Irene A. Stegun, eds. Manual de funciones matemáticas con fórmulas, gráficas y tablas matemáticas. Nueva York: Dover, 1972. (Ver Capítulo 7)
• "Formas de bucles de montaña rusa" . Consultado el 12 de noviembre de 2010 .

enlaces externos

• Weisstein, Eric W. "Espiral de Cornu". MundoMatemático .
• La espiral de Euler en curvas matemáticas bidimensionales
• Ejemplo interactivo con JSXGraph