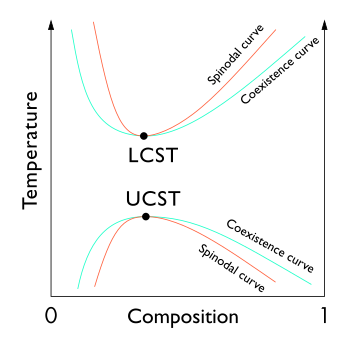
En termodinámica , el límite de estabilidad local frente a la separación de fases con respecto a pequeñas fluctuaciones está claramente definido por la condición de que la segunda derivada de la energía libre de Gibbs es cero.
El lugar geométrico de estos puntos (el punto de inflexión dentro de una curva Gx o Gc, energía libre de Gibbs en función de la composición ) se conoce como la curva espinodal . [1] [2] [3] Para composiciones dentro de esta curva, fluctuaciones infinitesimalmente pequeñas en la composición y la densidad conducirán a la separación de fases a través de la descomposición espinodal . Fuera de la curva, la solución será al menos metaestable con respecto a las fluctuaciones. [3] En otras palabras, fuera de la curva espinodal algún proceso cuidadoso puede obtener un sistema monofásico. [3] Dentro de ella, solo los procesos alejados del equilibrio termodinámico , como la deposición física de vapor , permitirán preparar composiciones monofásicas. [4] Los puntos locales de composiciones coexistentes, definidos por la construcción de tangente común, se conocen como curva de coexistencia binodal , que denota el estado de equilibrio de energía mínima del sistema. El aumento de la temperatura da como resultado una diferencia decreciente entre la entropía de mezcla y la entalpía de mezcla, y por lo tanto las composiciones coexistentes se acercan. La curva binodal constituye la base de la brecha de miscibilidad en un diagrama de fases. La energía libre de la mezcla cambia con la temperatura y la concentración, y la curva binodal y la espinodal se encuentran en la temperatura y composición críticas o de solución . [5]
Para soluciones binarias, el criterio termodinámico que define la curva espinodal es que la segunda derivada de la energía libre con respecto a la densidad o alguna variable de composición es cero. [3] [6] [7]
Los extremos del espinodal en un gráfico de temperatura vs composición coinciden con los de la curva binodal, y se conocen como puntos críticos . [7] El espinodal en sí puede considerarse como una línea de puntos pseudocríticos, con la función de correlación tomando una forma de escala con exponentes críticos no clásicos . [8] Estrictamente hablando, un espinodal se define como un objeto teórico de campo medio . Como tal, el espinodal no existe en sistemas reales, [9] pero se puede extrapolar para inferir la existencia de un pseudoespinodal que exhibe un comportamiento crítico como la desaceleración crítica . [10]
En el caso de equilibrios líquido-líquido isotérmicos ternarios, la curva espinodal (obtenida a partir de la matriz de Hesse) y el punto crítico correspondiente se pueden utilizar para ayudar al proceso de correlación de datos experimentales. [11] [12] [13]