Espacio-tiempo curvado

En física, el espacio-tiempo curvo es el modelo matemático en el que, con la teoría de la relatividad general de Einstein , surge naturalmente la gravedad, en lugar de ser descrita como una fuerza fundamental en el marco de referencia euclidiano estático de Newton . Los objetos se mueven a lo largo de geodésicas (trayectorias curvas determinadas por la geometría local del espacio-tiempo) en lugar de ser influenciados directamente por cuerpos distantes. Este marco condujo a dos principios fundamentales: la independencia de coordenadas, que afirma que las leyes de la física son las mismas independientemente del sistema de coordenadas utilizado, y el principio de equivalencia, que establece que los efectos de la gravedad son indistinguibles de los de la aceleración en regiones suficientemente pequeñas del espacio. Estos principios sentaron las bases para una comprensión más profunda de la gravedad a través de la geometría del espacio-tiempo, tal como se formaliza en las ecuaciones de campo de Einstein.

Introducción

Las teorías de Newton suponían que el movimiento se produce en el contexto de un marco de referencia euclidiano rígido que se extiende por todo el espacio y todo el tiempo. La gravedad está mediada por una fuerza misteriosa, que actúa instantáneamente a través de una distancia, cuyas acciones son independientes del espacio intermedio. ^{[nota 1]} Por el contrario, Einstein negó que exista un marco de referencia euclidiano de fondo que se extienda por todo el espacio. Tampoco existe nada parecido a una fuerza de gravitación, solo la estructura del espacio-tiempo en sí. ^[1]^{: 175–190}

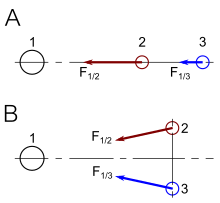
En términos de espacio-tiempo, la trayectoria de un satélite que orbita la Tierra no está determinada por las influencias distantes de la Tierra, la Luna y el Sol. En cambio, el satélite se mueve a través del espacio solo en respuesta a las condiciones locales. Dado que el espacio-tiempo es en todas partes localmente plano cuando se lo considera en una escala suficientemente pequeña, el satélite siempre sigue una línea recta en su marco inercial local. Decimos que el satélite siempre sigue la trayectoria de una geodésica . No se puede descubrir evidencia de que la gravitación siga los movimientos de una sola partícula. ^[1]^{: 175–190}

En cualquier análisis del espacio-tiempo, la evidencia de la gravitación requiere que se observen las aceleraciones relativas de dos cuerpos o dos partículas separadas. En la figura 5-1, dos partículas separadas, en caída libre en el campo gravitacional de la Tierra, exhiben aceleraciones de marea debido a inhomogeneidades locales en el campo gravitacional de modo que cada partícula sigue un camino diferente a través del espacio-tiempo. Las aceleraciones de marea que exhiben estas partículas entre sí no requieren fuerzas para su explicación. Más bien, Einstein las describió en términos de la geometría del espacio-tiempo, es decir, la curvatura del espacio-tiempo. Estas aceleraciones de marea son estrictamente locales. Es el efecto total acumulativo de muchas manifestaciones locales de curvatura lo que da como resultado la apariencia de una fuerza gravitacional que actúa a gran distancia de la Tierra. ^[1]^{: 175–190}

Distintos observadores que analizan los escenarios presentados en esta figura interpretan los escenarios de manera diferente según su conocimiento de la situación. (i) Un primer observador, en el centro de masa de las partículas 2 y 3 pero sin saber que la masa 1 es grande, concluye que existe una fuerza de repulsión entre las partículas en el escenario A, mientras que existe una fuerza de atracción entre las partículas en el escenario B. (ii) Un segundo observador, consciente de la gran masa 1, sonríe ante la ingenuidad del primer reportero. Este segundo observador sabe que, en realidad, las fuerzas aparentes entre las partículas 2 y 3 representan en realidad efectos de marea resultantes de su atracción diferencial por la masa 1. (iii) Un tercer observador, entrenado en relatividad general, sabe que, de hecho, no hay fuerzas en absoluto que actúen entre los tres objetos. Más bien, los tres objetos se mueven a lo largo de geodésicas en el espacio-tiempo.

Dos proposiciones centrales subyacen a la relatividad general.

El primer concepto crucial es la independencia de coordenadas: las leyes de la física no pueden depender del sistema de coordenadas que se utilice. Se trata de una importante ampliación del principio de relatividad a partir de la versión utilizada en la relatividad especial, que establece que las leyes de la física deben ser las mismas para todo observador que se mueva en sistemas de referencia no acelerados (inerciales). En la relatividad general, para utilizar las propias palabras de Einstein (traducidas), "las leyes de la física deben ser de tal naturaleza que se apliquen a sistemas de referencia en cualquier tipo de movimiento". ^[2]^{: 113} Esto nos lleva a un problema inmediato: en sistemas acelerados, uno siente fuerzas que aparentemente le permitirían evaluar su estado de aceleración en un sentido absoluto. Einstein resolvió este problema mediante el principio de equivalencia. ^[3]^{: 137–149}

El principio de equivalencia establece que en cualquier región suficientemente pequeña del espacio, los efectos de la gravitación son los mismos que los de la aceleración.
En la figura 5-2, la persona A está en una nave espacial, lejos de cualquier objeto masivo, que experimenta una aceleración uniforme de g . La persona B está en una caja que reposa sobre la Tierra. Siempre que la nave espacial sea suficientemente pequeña para que los efectos de marea no sean medibles (dada la sensibilidad de la instrumentación de medición de gravedad actual, A y B presumiblemente deberían ser liliputienses ), no hay experimentos que A y B puedan realizar que les permitan decir en qué entorno están. ^[3]^{: 141–149}
Una expresión alternativa del principio de equivalencia es señalar que en la ley de gravitación universal de Newton, F = GMm _g/r ² = m _gg y en la segunda ley de Newton, F = m _ia , no hay ninguna razón a priori por la que la masa gravitacional m _g deba ser igual a la masa inercial m _i . El principio de equivalencia establece que estas dos masas son idénticas. ^[3]^{: 141–149}

Para pasar de la descripción elemental del espacio-tiempo curvo que se acaba de mencionar a una descripción completa de la gravitación se requieren cálculos tensoriales y geometría diferencial, dos temas que requieren un estudio considerable. Sin estas herramientas matemáticas, es posible escribir sobre la relatividad general, pero no es posible demostrar ninguna derivación no trivial.

Curvatura del tiempo

En el debate sobre la relatividad especial, las fuerzas no desempeñaron más que un papel secundario. La relatividad especial presupone la capacidad de definir marcos inerciales que llenen todo el espacio-tiempo, cuyos relojes funcionen al mismo ritmo que el reloj del origen. ¿Es esto realmente posible? En un campo gravitatorio no uniforme, la experiencia dicta que la respuesta es no. Los campos gravitatorios hacen imposible construir un marco inercial global . En regiones suficientemente pequeñas del espacio-tiempo, los marcos inerciales locales aún son posibles. La relatividad general implica la unión sistemática de estos marcos locales para formar una imagen más general del espacio-tiempo. ^[4]^{: 118–126}

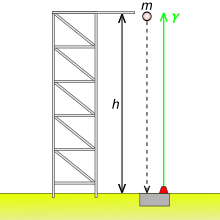
Años antes de la publicación de la teoría general en 1916, Einstein utilizó el principio de equivalencia para predecir la existencia del corrimiento al rojo gravitacional en el siguiente experimento mental : (i) Supongamos que se ha construido una torre de altura h (Fig. 5-3). (ii) Dejemos caer una partícula de masa en reposo m desde lo alto de la torre. Cae libremente con aceleración g , alcanzando el suelo con velocidad $v = (2 gh) 1/2$ , de modo que su energía total E , medida por un observador en el suelo, es ⁠ ⁠ $m+{{\tfrac {1}{2}}mv^{2}}/{c^{2}}=m+{mgh}/{c^{2}}$ (iii) Un convertidor de masa-energía transforma la energía total de la partícula en un único fotón de alta energía, que dirige hacia arriba. (iv) En lo alto de la torre, un convertidor de energía-masa transforma la energía del fotón E ' de nuevo en una partícula de masa en reposo m ' . ^[4]^{: 118–126}

Debe ser que $m = m'$ , ya que de lo contrario se podría construir un dispositivo de movimiento perpetuo . Por lo tanto, predecimos que $E' = m$ , de modo que

{\frac {E'}{E}}={\frac {h\nu \,'}{h\nu }}={\frac {m}{m+{\frac {mgh}{c^ {2}}}}}=1-{\frac {gh}{c^{2}}}

Un fotón que asciende por el campo gravitatorio de la Tierra pierde energía y se desplaza hacia el rojo. Los primeros intentos de medir este desplazamiento hacia el rojo mediante observaciones astronómicas no fueron concluyentes, pero las observaciones de laboratorio definitivas las realizaron Pound y Rebka (1959) y, posteriormente, Pound y Snider (1964). ^[5]

La luz tiene una frecuencia asociada, y esta frecuencia puede utilizarse para controlar el funcionamiento de un reloj. El corrimiento al rojo gravitacional conduce a una conclusión importante sobre el tiempo en sí: la gravedad hace que el tiempo transcurra más lento. Supongamos que construimos dos relojes idénticos cuyas velocidades están controladas por alguna transición atómica estable. Colocamos un reloj en lo alto de la torre, mientras el otro reloj permanece en el suelo. Un experimentador en lo alto de la torre observa que las señales del reloj de tierra tienen una frecuencia más baja que las del reloj que está a su lado en la torre. La luz que sube por la torre es simplemente una onda, y es imposible que las crestas de onda desaparezcan en el camino hacia arriba. A la cima de la torre llegan exactamente tantas oscilaciones de luz como las que se emitieron en la base. El experimentador concluye que el reloj de tierra va más lento, y puede confirmarlo bajando el reloj de la torre para compararlo lado a lado con el reloj de tierra. ^[6]^{: 16–18} Para una torre de 1 km, la discrepancia ascendería a unos 9,4 nanosegundos por día, fácilmente medible con instrumentación moderna.

Los relojes en un campo gravitatorio no funcionan todos al mismo ritmo. Experimentos como el experimento de Pound-Rebka han establecido firmemente la curvatura del componente temporal del espacio-tiempo. El experimento de Pound-Rebka no dice nada sobre la curvatura del componente espacial del espacio-tiempo. Pero los argumentos teóricos que predicen la dilatación gravitatoria del tiempo no dependen en absoluto de los detalles de la relatividad general. Cualquier teoría de la gravedad predecirá la dilatación gravitatoria del tiempo si respeta el principio de equivalencia. ^[6]^{: 16} Esto incluye la gravitación newtoniana. Una demostración estándar en relatividad general es mostrar cómo, en el " límite newtoniano " (es decir, las partículas se mueven lentamente, el campo gravitatorio es débil y el campo es estático), la curvatura del tiempo por sí sola es suficiente para derivar la ley de la gravedad de Newton. ^[7]^{: 101–106}

La gravitación newtoniana es una teoría del tiempo curvo. La relatividad general es una teoría del tiempo curvo y del espacio curvo. Dada G como la constante gravitacional, M como la masa de una estrella newtoniana y cuerpos en órbita de masa insignificante a una distancia r de la estrella, el intervalo espacio-temporal para la gravitación newtoniana es aquel para el cual solo el coeficiente de tiempo es variable: ^[6]^{: 229–232}

\Delta s^{2}=\left(1-{\frac {2GM}{c^{2}r}}\right)(c\Delta t)^{2}-\,(\Delta x)^{2}-(\Delta y)^{2}-(\Delta z)^{2}

Curvatura del espacio

El coeficiente que se encuentra delante de describe la curvatura del tiempo en la gravitación newtoniana, y esta curvatura explica por completo todos los efectos gravitacionales newtonianos. Como se esperaba, este factor de corrección es directamente proporcional a y , y debido a que en el denominador, el factor de corrección aumenta a medida que uno se acerca al cuerpo gravitatorio, lo que significa que el tiempo es curvo. $(1-2GM/(c^{2}r))$ $(c\Delta t)^{2}$ ${\estilo de visualización G}$ ${\estilo de visualización M}$ ${\estilo de visualización r}$

Pero la relatividad general es una teoría del espacio curvo y del tiempo curvo, de modo que si hay términos que modifican los componentes espaciales del intervalo espacio-temporal presentado anteriormente, ¿no deberían verse sus efectos en, por ejemplo, las órbitas planetarias y satelitales debido a los factores de corrección de curvatura aplicados a los términos espaciales?

La respuesta es que se ven , pero los efectos son minúsculos. La razón es que las velocidades planetarias son extremadamente pequeñas comparadas con la velocidad de la luz, de modo que para los planetas y satélites del sistema solar, el término eclipsa los términos espaciales. ^[6]^{: 234–238} $(c\Delta t)^{2}$

A pesar de la minuciosidad de los términos espaciales, las primeras indicaciones de que algo andaba mal con la gravitación newtoniana se descubrieron hace más de un siglo y medio. En 1859, Urbain Le Verrier , en un análisis de las observaciones cronometradas disponibles de los tránsitos de Mercurio sobre el disco solar desde 1697 hasta 1848, informó que la física conocida no podía explicar la órbita de Mercurio, a menos que posiblemente existiera un planeta o cinturón de asteroides dentro de la órbita de Mercurio. El perihelio de la órbita de Mercurio exhibió un exceso de tasa de precesión sobre la que podría explicarse por los tirones de los otros planetas. ^[8] La capacidad de detectar y medir con precisión el valor minúsculo de esta precesión anómala (solo 43 segundos de arco por siglo tropical ) es testimonio de la sofisticación de la astrometría del siglo XIX .

El anuncio de Le Verrier, el astrónomo que había descubierto antes la existencia de Neptuno "con la punta de su pluma" al analizar las irregularidades en la órbita de Urano, desencadenó un período de "vulcanomanía" que duró dos décadas, durante las cuales tanto astrónomos profesionales como aficionados buscaron el hipotético nuevo planeta. Esta búsqueda incluyó varios avistamientos falsos de Vulcano. Finalmente se estableció que no existía tal planeta ni cinturón de asteroides. ^[9]

En 1916, Einstein demostró que esta precesión anómala de Mercurio se explica por los términos espaciales de la curvatura del espacio-tiempo. La curvatura en el término temporal, al ser simplemente una expresión de la gravitación newtoniana, no tiene ningún papel en la explicación de esta precesión anómala. El éxito de su cálculo fue una poderosa indicación para los colegas de Einstein de que la teoría general de la relatividad podía ser correcta.

La predicción más espectacular de Einstein fue su cálculo de que los términos de curvatura en los componentes espaciales del intervalo espacio-temporal podían medirse en la curvatura de la luz alrededor de un cuerpo masivo. La luz tiene una pendiente de ±1 en un diagrama espacio-temporal. Su movimiento en el espacio es igual a su movimiento en el tiempo. Para la expresión de campo débil del intervalo invariante, Einstein calculó una curvatura exactamente igual pero de signo opuesto en sus componentes espaciales. ^[6]^{: 234–238}

\Delta s^{2}=\left(1-{\frac {2GM}{c^{2}r}}\right)(c\Delta t)^{2}

-\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]

En la gravitación de Newton, el coeficiente que se encuentra delante de predice la curvatura de la luz alrededor de una estrella. En la relatividad general, el coeficiente que se encuentra delante de predice una duplicación de la curvatura total. ^[6]^{: 234–238} $(1-2GM/(c^{2}r))$ $(c\Delta t)^{2}$ $(1+2GM/(c^{2}r))$ $\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]$

La historia de la expedición del eclipse de Eddington de 1919 y el ascenso de Einstein a la fama están bien contados en otros lugares. ^[10]

Fuentes de la curvatura del espacio-tiempo

En la teoría de la gravitación de Newton , la única fuente de fuerza gravitacional es la masa .

En cambio, la relatividad general identifica varias fuentes de curvatura del espacio-tiempo además de la masa. En las ecuaciones de campo de Einstein , las fuentes de gravedad se presentan en el lado derecho del tensor de tensión-energía . ^[11] $T_{\mu \nu},$

La figura 5-5 clasifica las distintas fuentes de gravedad en el tensor de tensión-energía:

${\estilo de visualización T^{00}}$ (rojo): La densidad total de masa-energía, incluidas todas las contribuciones a la energía potencial de las fuerzas entre las partículas, así como la energía cinética de los movimientos térmicos aleatorios.
$Estilo de visualización T^{0i}}$ y (naranja): estos son términos de densidad de momento. Incluso si no hay movimiento en masa, la energía puede transmitirse por conducción de calor y la energía conducida transportará momento. $Estilo de visualización T^{i0}}$
$Estilo de visualización T^{ij}}$ son las tasas de flujo del componente i del momento por unidad de área en la dirección j . Incluso si no hay movimiento en masa, los movimientos térmicos aleatorios de las partículas darán lugar a un flujo de momento, por lo que los términos $i = j$ (verdes) representan la presión isotrópica y los términos $i \neq j$ (azules) representan las tensiones de corte. ^[11]

Una conclusión importante que se deriva de las ecuaciones es que, coloquialmente hablando, la gravedad en sí misma crea gravedad . ^{[nota 2]} La energía tiene masa. Incluso en la gravedad newtoniana, el campo gravitacional está asociado con una energía, llamada $E=mgh,$ energía potencial gravitacional . En la relatividad general, la energía del campo gravitacional retroalimenta la creación del campo gravitacional. Esto hace que las ecuaciones no sean lineales y difíciles de resolver en cualquier caso que no sea de campo débil. ^[6]^{: 240} La relatividad numérica es una rama de la relatividad general que utiliza métodos numéricos para resolver y analizar problemas, a menudo empleando supercomputadoras para estudiar agujeros negros , ondas gravitacionales , estrellas de neutrones y otros fenómenos en el régimen de campo fuerte.

Impulso energético

Figura 5-6. (izquierda) La masa-energía deforma el espacio-tiempo. (derecha) Las distribuciones de masa-energía rotatorias con momento angular J generan campos gravitomagnéticos H .

En la relatividad especial, la masa-energía está estrechamente relacionada con el momento . Así como el espacio y el tiempo son aspectos diferentes de una entidad más amplia llamada espacio-tiempo, la masa-energía y el momento son simplemente aspectos diferentes de una cantidad unificada de cuatro dimensiones llamada cuatro-momento . En consecuencia, si la masa-energía es una fuente de gravedad, el momento también debe ser una fuente. La inclusión del momento como fuente de gravedad conduce a la predicción de que las masas en movimiento o rotatorias pueden generar campos análogos a los campos magnéticos generados por cargas en movimiento, un fenómeno conocido como gravitomagnetismo . ^[12]

Es bien sabido que la fuerza del magnetismo se puede deducir aplicando las reglas de la relatividad especial a cargas en movimiento. (Feynman presentó una demostración elocuente de esto en el volumen II, capítulo 13-6 de sus Lecciones de física , disponibles en línea). ^[13] Se puede utilizar la lógica análoga para demostrar el origen del gravitomagnetismo. ^[6]^{: 245–253}

En la figura 5-7a, dos corrientes paralelas infinitamente largas de partículas masivas tienen velocidades iguales y opuestas − v y + v en relación con una partícula de prueba en reposo y centrada entre las dos. Debido a la simetría de la configuración, la fuerza neta sobre la partícula central es cero. Suponga que ⁠ ⁠ $v\ll c$ de modo que las velocidades son simplemente aditivas. La figura 5-7b muestra exactamente la misma configuración, pero en el marco de la corriente superior. La partícula de prueba tiene una velocidad de + v , y la corriente inferior tiene una velocidad de +2 v . Dado que la situación física no ha cambiado, solo el marco en el que se observan las cosas, la partícula de prueba no debería ser atraída hacia ninguna de las corrientes. ^[6]^{: 245–253}

No está del todo claro que las fuerzas ejercidas sobre la partícula de prueba sean iguales. (1) Puesto que la corriente inferior se mueve más rápido que la superior, cada partícula en la corriente inferior tiene una energía de masa mayor que una partícula en la superior. (2) Debido a la contracción de Lorentz, hay más partículas por unidad de longitud en la corriente inferior que en la corriente superior. (3) Otra contribución a la masa gravitacional activa de la corriente inferior proviene de un término de presión adicional que, en este punto, no tenemos antecedentes suficientes para discutir. Todos estos efectos juntos aparentemente exigirían que la partícula de prueba sea atraída hacia la corriente inferior. ^[6]^{: 245–253}

La partícula de prueba no es atraída hacia la corriente inferior debido a una fuerza dependiente de la velocidad que sirve para repeler una partícula que se mueve en la misma dirección que la corriente inferior. Este efecto gravitacional dependiente de la velocidad es el gravitomagnetismo. ^[6]^{: 245–253}

La materia en movimiento a través de un campo gravitomagnético está sujeta, por lo tanto, a los llamados efectos de arrastre de marco análogos a la inducción electromagnética . Se ha propuesto que dichas fuerzas gravitomagnéticas subyacen a la generación de los chorros relativistas (Fig. 5-8) expulsados por algunos agujeros negros supermasivos en rotación . ^[14]^[15]

Presión y estrés

Las cantidades que están directamente relacionadas con la energía y el momento también deberían ser fuentes de gravedad, a saber, la presión interna y la tensión . En conjunto, la masa-energía , el momento, la presión y la tensión sirven como fuentes de gravedad: colectivamente, son lo que le dice al espacio-tiempo cómo curvarse.

La relatividad general predice que la presión actúa como una fuente gravitatoria con exactamente la misma fuerza que la densidad de masa-energía. La inclusión de la presión como fuente de gravedad conduce a diferencias dramáticas entre las predicciones de la relatividad general y las de la gravitación newtoniana. Por ejemplo, el término de presión establece un límite máximo para la masa de una estrella de neutrones . Cuanto más masiva sea una estrella de neutrones, más presión se requiere para soportar su peso contra la gravedad. Sin embargo, el aumento de la presión se suma a la gravedad que actúa sobre la masa de la estrella. Por encima de cierta masa determinada por el límite de Tolman-Oppenheimer-Volkoff , el proceso se descontrola y la estrella de neutrones colapsa en un agujero negro . ^[6]^{: 243, 280}

Los términos de estrés se vuelven muy significativos cuando se realizan cálculos como simulaciones hidrodinámicas de supernovas con colapso de núcleo. ^[16]

Estas predicciones sobre el papel de la presión, el momento y el estrés como fuentes de la curvatura del espacio-tiempo son elegantes y desempeñan un papel importante en la teoría. En lo que respecta a la presión, el universo primitivo estaba dominado por la radiación ^[17] y es muy poco probable que cualquiera de los datos cosmológicos relevantes (por ejemplo, las abundancias de nucleosíntesis , etc.) pudieran reproducirse si la presión no contribuyera a la gravedad, o si no tuviera la misma fuerza como fuente de gravedad que la masa-energía. Del mismo modo, la consistencia matemática de las ecuaciones de campo de Einstein se rompería si los términos de estrés no contribuyeran como fuente de gravedad.

Prueba experimental de las fuentes de curvatura del espacio-tiempo

Definiciones: Masa activa, pasiva e inercial.

Bondi distingue entre diferentes tipos posibles de masa: (1) masa activa ( ) $Estilo de visualización m_{a}$ es la masa que actúa como fuente de un campo gravitacional; (2) masa pasiva ( ) $estilo de visualización m_{p}}$ es la masa que reacciona a un campo gravitacional; (3) masa inercial ( ) $Estilo de visualización m_{i}}$ es la masa que reacciona a la aceleración. ^[18]

$estilo de visualización m_{p}}$ es lo mismo que la masa gravitacional ( ) $Estilo de visualización mg$ en la discusión del principio de equivalencia.

En la teoría newtoniana,

La tercera ley de acción y reacción dicta que y debe ser lo mismo. $Estilo de visualización m_{a}$ $estilo de visualización m_{p}}$
Por otra parte, si y son iguales es un resultado empírico. $estilo de visualización m_{p}}$ $Estilo de visualización m_{i}}$

En relatividad general,

La igualdad de y está dictada por el principio de equivalencia. $estilo de visualización m_{p}}$ $Estilo de visualización m_{i}}$
No existe ningún principio de "acción y reacción" que dicte alguna relación necesaria entre y . ^[18] $Estilo de visualización m_{a}$ $estilo de visualización m_{p}}$

La presión como fuente gravitacional

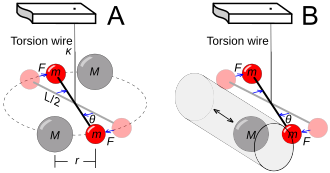
El experimento clásico para medir la fuerza de una fuente gravitacional (es decir, su masa activa) fue realizado por primera vez en 1797 por Henry Cavendish (Fig. 5-9a). Dos bolas pequeñas pero densas están suspendidas en un alambre fino, formando una balanza de torsión . Al acercar dos masas de prueba grandes a las bolas se introduce un par de torsión detectable. Dadas las dimensiones del aparato y la constante de resorte medible del alambre de torsión, se puede determinar la constante gravitacional G.

Estudiar los efectos de la presión comprimiendo las masas de prueba es inútil, porque las presiones de laboratorio alcanzables son insignificantes en comparación con la masa-energía de una bola de metal.

Sin embargo, las presiones electromagnéticas repulsivas resultantes de los protones que se encuentran fuertemente apretados dentro de los núcleos atómicos son típicamente del orden de 10 ²⁸ atm ≈ 10 ³³ Pa ≈ 10 ³³ kg·s ⁻² m ⁻¹ . Esto equivale a alrededor del 1% de la densidad de masa nuclear de aproximadamente 10 ¹⁸ kg/m ³ (después de factorizar c ² ≈ 9×10 ¹⁶ m ² s ⁻² ). ^[19]

Figura 5-10. Experimento de medición de distancias por láser en la Luna. (izquierda) Este retrorreflector fue dejado en la Luna por los astronautas de la misión Apolo 11. (derecha) Astrónomos de todo el mundo han hecho rebotar la luz láser en los retrorreflectores dejados por los astronautas de las misiones Apolo y los vehículos lunares rusos para medir con precisión la distancia entre la Tierra y la Luna.

Si la presión no actúa como una fuente gravitacional, entonces la relación debería ser menor para los núcleos con un número atómico mayor Z , en los que las presiones electrostáticas son más altas. LB Kreuzer (1968) realizó un experimento Cavendish utilizando una masa de teflón suspendida en una mezcla de los líquidos tricloroetileno y dibromoetano que tienen la misma densidad de flotación que el teflón (Fig. 5-9b). El flúor tiene un número atómico $Z$ $= 9$ , mientras que el bromo tiene $Z$ $= 35$ . Kreuzer descubrió que reposicionar la masa de teflón no causaba ninguna desviación diferencial de la barra de torsión, estableciendo así que la masa activa y la masa pasiva eran equivalentes con una precisión de 5×10 ⁻⁵ . ^[20] $Estilo de visualización m_{a}/m_{p}$

Aunque Kreuzer originalmente consideró este experimento simplemente como una prueba de la relación entre la masa activa y la masa pasiva, Clifford Will (1976) reinterpretó el experimento como una prueba fundamental del acoplamiento de fuentes a campos gravitacionales. ^[21]

En 1986, Bartlett y Van Buren observaron que el sistema de medición de distancias láser lunar había detectado un desfase de 2 km entre el centro de la figura de la Luna y su centro de masas. Esto indica una asimetría en la distribución de Fe (abundante en el núcleo de la Luna) y Al (abundante en su corteza y manto). Si la presión no contribuyera de igual manera a la curvatura del espacio-tiempo como lo hace la masa-energía, la Luna no estaría en la órbita predicha por la mecánica clásica. Utilizaron sus mediciones para ajustar los límites de cualquier discrepancia entre la masa activa y pasiva a aproximadamente 10 ⁻¹² . ^[22] Con décadas de datos adicionales de medición de distancias láser lunares, Singh et al. (2023) informaron una mejora de estos límites en un factor de aproximadamente 100. ^[23]

Gravitomagnetismo

La existencia del gravitomagnetismo fue demostrada por Gravity Probe B (GP-B) , una misión basada en satélite que se lanzó el 20 de abril de 2004. ^[24] La fase de vuelo espacial duró hasta2005El objetivo de la misión era medir la curvatura del espacio-tiempo cerca de la Tierra, con especial énfasis en el gravitomagnetismo .

Los resultados iniciales confirmaron el efecto geodésico relativamente grande (que se debe a la simple curvatura del espacio-tiempo y también se conoce como precesión de De Sitter) con una precisión de alrededor del 1%. El efecto de arrastre de marco mucho más pequeño (que se debe al gravitomagnetismo y también se conoce como precesión de Lense-Thirring ) fue difícil de medir debido a los efectos de carga inesperados que causaban una deriva variable en los giroscopios. Sin embargo,Agosto de 2008, el efecto de arrastre de trama se había confirmado dentro del 15% del resultado esperado, ^[25] mientras que el efecto geodésico se confirmó en mejor del 0,5%. ^[26]^[27]

Las mediciones posteriores del arrastre de cuadros mediante observaciones de alcance láser de los satélites LARES , LAGEOS -1 y LAGEOS-2 han mejorado la medición GP-B , con resultados (a partir de 2016) que demuestran el efecto dentro del 5% de su valor teórico, ^[28] aunque ha habido cierto desacuerdo sobre la precisión de este resultado. ^[29]

Otro esfuerzo, el experimento de Giroscopios en Relatividad General (GINGER), busca utilizar tres láseres de anillo de 6 m montados en ángulos rectos entre sí a 1400 m por debajo de la superficie de la Tierra para medir este efecto. ^[30]^[31] Los primeros diez años de experiencia con un prototipo de conjunto de giroscopios láser de anillo, GINGERINO, establecieron que el experimento a escala real debería poder medir el gravitomagnetismo debido a la rotación de la Tierra con una precisión de 0,1% o incluso mejor. ^[32]

Véase también

Topología del espacio-tiempo

Notas

^ Newton mismo era muy consciente de las dificultades inherentes a estas suposiciones, pero en la práctica, hacer estas suposiciones era la única manera en que podía avanzar. En 1692, escribió a su amigo Richard Bentley: "Que la gravedad sea innata, inherente y esencial a la materia, de modo que un cuerpo pueda actuar sobre otro a distancia a través del vacío, sin la mediación de ninguna otra cosa, por y a través de la cual su acción y fuerza puedan transmitirse de uno a otro, es para mí un absurdo tan grande que creo que ningún hombre que tenga en cuestiones filosóficas una facultad competente de pensamiento puede caer jamás en él".
^ Más precisamente, el campo gravitatorio se acopla consigo mismo. En la gravedad newtoniana, el potencial debido a dos masas puntuales es simplemente la suma de los potenciales de las dos masas, pero esto no se aplica a la RG. Esto puede considerarse como el resultado del principio de equivalencia: si la gravitación no se acoplara consigo misma, dos partículas unidas por su atracción gravitatoria mutua no tendrían la misma masa inercial (debido a la energía de enlace negativa) que su masa gravitatoria. ^[7]^{: 112–113}

Referencias

^ abc Taylor, Edwin F.; Wheeler, John Archibald (1992). Física del espacio-tiempo: Introducción a la relatividad especial (2.ª ed.). San Francisco, California: Freeman. ISBN 0-7167-0336-X. Recuperado el 14 de abril de 2017 .
^ Lorentz, HA; Einstein, A.; Minkowski, H.; Weyl, H. (1952). El principio de relatividad: una colección de memorias originales sobre la teoría especial y general de la relatividad . Publicaciones de Dover. ISBN 0-486-60081-5.
^ abc Mook, Delo E.; Vargish, Thoma s (1987). Inside Relativity. Princeton, Nueva Jersey: Princeton University Press. ISBN 0-691-08472-6.
^ ab Schutz, Bernard F. (1985). Un primer curso de relatividad general . Cambridge, Reino Unido: Cambridge University Press. p. 26. ISBN 0-521-27703-5.
^ Mester, John. «Experimental Tests of General Relativity» (PDF) . Laboratoire Univers et Théories. Archivado desde el original (PDF) el 18 de marzo de 2017. Consultado el 9 de junio de 2017 .
^ abcdefghijkl Schutz, Bernard (2004). Gravedad desde cero: una guía introductoria a la gravedad y la relatividad general (edición reimpresa). Cambridge: Cambridge University Press . ISBN 0-521-45506-5Archivado desde el original el 17 de enero de 2023 . Consultado el 24 de mayo de 2017 .
^ ab Carroll, Sean M. (2 de diciembre de 1997). "Notas de clase sobre relatividad general". arXiv : gr-qc/9712019 .
^ Le Verrier, Urbano (1859). "Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète". Comptes rendus hebdomadaires des séances de l'Académie des Sciences . 49 : 379–383.
^ Worrall, Simon (4 de noviembre de 2015). «La búsqueda de Vulcano, el planeta que no existía». National Geographic . Archivado desde el original el 24 de mayo de 2017.
^ Levine, Alaina G. (mayo de 2016). «29 de mayo de 1919: Eddington observa un eclipse solar para poner a prueba la relatividad general». Este mes en la historia de la física. APS News . American Physical Society. Archivado desde el original el 2 de junio de 2017.
^ ab Hobson, MP; Efstathiou, G.; Lasenby, AN (2006). Relatividad general . Cambridge: Cambridge University Press. págs. 176–179. ISBN 978-0-521-82951-9.
^ Thorne, Kip S. (1988). Fairbank, JD; Deaver, BS Jr.; Everitt, WF; Michelson, PF (eds.). Cerca de cero: nuevas fronteras de la física (PDF) . WH Freeman and Company. págs. 573–586. S2CID 12925169. Archivado desde el original (PDF) el 28 de julio de 2017.
^ Feynman, RP; Leighton, RB; Sands, M. (1964). Las conferencias Feynman sobre física, vol. 2 (edición New Millenium). Basic Books. págs. 13-6 a 13-11. ISBN 978-0-465-02416-2Archivado desde el original el 17 de enero de 2023 . Consultado el 1 de julio de 2017 .
^ Williams, RK (1995). "Extracción de rayos X, rayos Ύ y pares e ⁻ –e ⁺ relativistas de agujeros negros supermasivos de Kerr utilizando el mecanismo de Penrose". Physical Review D . 51 (10): 5387–5427. Bibcode :1995PhRvD..51.5387W. doi :10.1103/PhysRevD.51.5387. PMID 10018300.
^ Williams, RK (2004). "Chorros polares colimados de escape vorticiales e ⁻ –e ⁺ producidos intrínsecamente por agujeros negros en rotación y procesos de Penrose". The Astrophysical Journal . 611 (2): 952–963. arXiv : astro-ph/0404135 . Bibcode :2004ApJ...611..952W. doi :10.1086/422304. S2CID 1350543.
^ Kuroda, Takami; Kotake, Kei; Takiwaki, Tomoya (2012). "Simulaciones relativistas totalmente generales de supernovas de colapso de núcleo con un transporte aproximado de neutrinos". The Astrophysical Journal . 755 (1): 11. arXiv : 1202.2487 . Bibcode :2012ApJ...755...11K. doi :10.1088/0004-637X/755/1/11. S2CID 119179339.
^ Wollack, Edward J. (10 de diciembre de 2010). «Cosmología: el estudio del universo». Universo 101: teoría del Big Bang . NASA . Archivado desde el original el 14 de mayo de 2011. Consultado el 15 de abril de 2017 .
^ ab Bondi, Hermann (1957). DeWitt, Cecile M.; Rickles, Dean (eds.). El papel de la gravitación en la física: Informe de la Conferencia de Chapel Hill de 1957. Berlín, Alemania: Biblioteca de Investigación Max Planck. pp. 159–162. ISBN 978-3-86931-963-6Archivado desde el original el 28 de julio de 2017 . Consultado el 1 de julio de 2017 .
^ Crowell, Benjamin (2000). Relatividad general. Fullerton, CA: Luz y materia. pp. 241–258. Archivado desde el original el 18 de junio de 2017 . Consultado el 30 de junio de 2017 .
^ Kreuzer, LB (1968). "Medición experimental de la equivalencia de masa gravitacional activa y pasiva". Physical Review . 169 (5): 1007–1011. Código Bibliográfico :1968PhRv..169.1007K. doi :10.1103/PhysRev.169.1007.
^ Will, CM (1976). "Masa activa en la gravedad relativista: interpretación teórica del experimento de Kreuzer". The Astrophysical Journal . 204 : 224–234. Bibcode :1976ApJ...204..224W. doi : 10.1086/154164 . Archivado desde el original el 28 de septiembre de 2018 . Consultado el 2 de julio de 2017 .
^ Bartlett, DF; Van Buren, Dave (1986). "Equivalencia de masa gravitacional activa y pasiva utilizando la luna". Physical Review Letters . 57 (1): 21–24. Bibcode :1986PhRvL..57...21B. doi :10.1103/PhysRevLett.57.21. PMID 10033347.
^ Singh, Vishwa Vijay; Müller, Jürgen; Biskupek, Liliane; Hackmann, Eva; Lämmerzahl, Claus (2023). "Equivalencia de masa gravitacional activa y pasiva probada con medición de distancia por láser lunar". Physical Review Letters . 131 (2): 021401. arXiv : 2212.09407 . Código Bibliográfico :2023PhRvL.131b1401S. doi :10.1103/PhysRevLett.131.021401. PMID 37505941 . Consultado el 7 de marzo de 2024 .
^ "Gravity Probe B: FAQ". Archivado desde el original el 2 de junio de 2018 . Consultado el 2 de julio de 2017 .
^ Gugliotta, G. (16 de febrero de 2009). «La perseverancia está dando sus frutos para poner a prueba la relatividad en el espacio». New York Times . Archivado desde el original el 3 de septiembre de 2018. Consultado el 2 de julio de 2017 .
^ Everitt, CWF; Parkinson, BW (2009). «Gravity Probe B Science Results—NASA Final Report» (PDF) . Archivado (PDF) del original el 23 de octubre de 2012. Consultado el 2 de julio de 2017 .
^ Everitt; et al. (2011). "Gravity Probe B: Resultados finales de un experimento espacial para probar la relatividad general". Physical Review Letters . 106 (22): 221101. arXiv : 1105.3456 . Código Bibliográfico :2011PhRvL.106v1101E. doi :10.1103/PhysRevLett.106.221101. PMID 21702590. S2CID 11878715.
^ Ciufolini, Ignazio; Paolozzi, Antonio Rolf Koenig; Pavlis, Erricos C.; Koenig, Rolf (2016). "Una prueba de la relatividad general utilizando los satélites LARES y LAGEOS y un modelo de gravedad terrestre GRACE". European Physical Journal C . 76 (3): 120. arXiv : 1603.09674 . Bibcode :2016EPJC...76..120C. doi :10.1140/epjc/s10052-016-3961-8. PMC 4946852 . PMID 27471430.
^ Iorio, L. (febrero de 2017). "Un comentario sobre "Una prueba de la relatividad general utilizando los satélites LARES y LAGEOS y un modelo de gravedad terrestre GRACE. Medición del arrastre de los marcos inerciales por la Tierra", por I. Ciufolini et al". The European Physical Journal C . 77 (2): 73. arXiv : 1701.06474 . Bibcode :2017EPJC...77...73I. doi :10.1140/epjc/s10052-017-4607-1. S2CID 118945777.
^ Cartlidge, Edwin (20 de enero de 2016). «Los láseres de anillo subterráneos pondrán a prueba la relatividad general». physicsworld.com . Instituto de Física. Archivado desde el original el 12 de julio de 2017 . Consultado el 2 de julio de 2017 .
^ "Einstein acertó al utilizar los sensores de rotación de la Tierra más sensibles jamás fabricados". Phys.org . Red Science X. Archivado desde el original el 10 de mayo de 2017 . Consultado el 2 de julio de 2017 .
^ Altucci, C.; Bajardi, F.; Basti, A.; Beverini, N.; Capozziello, S. (2021). El proyecto Ginger: resultados preliminares. Actas de la reunión MG16 sobre relatividad general en línea; 5-10 de julio de 2021. págs. 3956-3962. doi :10.1142/9789811269776_0329. ISBN 978-981-12-6977-6. Recuperado el 7 de septiembre de 2024 .