Delta-v

Delta- v (también conocido como " cambio en la velocidad "), simbolizado y pronunciado deltah-vee , tal como se utiliza en la dinámica de vuelo de naves espaciales , es una medida del impulso por unidad de masa de la nave espacial que se necesita para realizar una maniobra como el lanzamiento o aterrizaje en un planeta o luna, o una maniobra orbital en el espacio . Es un escalar que tiene las unidades de velocidad . Tal como se utiliza en este contexto, no es lo mismo que el cambio físico en la velocidad de dicha nave espacial. ${\textstyle {\Delta v}}$

Un ejemplo sencillo podría ser el caso de una nave espacial convencional propulsada por cohetes, que logra su empuje quemando combustible. El delta- v de una nave espacial de este tipo sería, entonces, el cambio de velocidad que la nave espacial puede alcanzar quemando toda su carga de combustible.

El delta- v se produce mediante motores de reacción , como los motores de cohetes , y es proporcional al empuje por unidad de masa y al tiempo de combustión. Se utiliza para determinar la masa de propulsor necesaria para la maniobra dada a través de la ecuación de cohetes de Tsiolkovsky .

Para maniobras múltiples, delta- v se suma linealmente.

Para las misiones interplanetarias, el delta- v se representa a menudo en un gráfico porkchop , que muestra el delta- v de la misión requerida en función de la fecha de lanzamiento.

Definición

$\Delta {v}=\int _{t_{0}}^{t_{1}}{\frac {|T(t)|}{m(t)}}\,dt$ dónde

$T (t) es el$ empuje instantáneoen el tiempo $t$ .
$m (t)$ es la masa instantánea en el tiempo $t$ .

El cambio de velocidad es útil en muchos casos, como para determinar el cambio de momento ( impulso ), donde: , donde es el momento y m es la masa. $\Delta \mathbf {p} =m\Delta \mathbf {v}$ $\mathbf {p}$

Casos específicos

En ausencia de fuerzas externas: donde es la coordenada aceleración. $\Delta {v}=\int _{t_{0}}^{t_{1}}\izquierda|{\dot {v}}\derecha|\,dt$ ${\punto {v}}$

Cuando se aplica empuje en una dirección constante ( $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠en/| en |⁠$ es constante) esto se simplifica a: que es simplemente la magnitud del cambio en la velocidad . Sin embargo, esta relación no se cumple en el caso general: si, por ejemplo, una aceleración constante y unidireccional se invierte después de $($ $t$ $1$ $-$ $t$ $0$ $)/2$ entonces la diferencia de velocidad es 0, pero delta- v es el mismo que para el empuje no invertido. $\Delta {v}=|v_{1}-v_{0}|$

En el caso de los cohetes, se entiende por "ausencia de fuerzas externas" la ausencia de resistencia gravitatoria y atmosférica, así como la ausencia de contrapresión aerostática en la boquilla, y por lo tanto se utiliza el vacío I _sp para calcular la capacidad delta- v del vehículo mediante la ecuación del cohete . Además, los costos de las pérdidas atmosféricas y la resistencia gravitatoria se suman al presupuesto delta- v cuando se trata de lanzamientos desde una superficie planetaria. ^[1]

Maniobras orbitales

Las maniobras orbitales se realizan activando un propulsor para producir una fuerza de reacción que actúa sobre la nave espacial. La magnitud de esta fuerza será

dónde

$v exh$ es la velocidad del gas de escape en el armazón del cohete
$ρ$ es el caudal de propulsor a la cámara de combustión

La aceleración de la nave espacial causada por esta fuerza será ${\punto {v}}$

donde $m$ es la masa de la nave espacial

Durante la combustión, la masa de la nave espacial disminuirá debido al uso de combustible, siendo la derivada temporal de la masa

Si ahora la dirección de la fuerza, es decir, la dirección de la boquilla , se fija durante la combustión, se obtiene el aumento de velocidad de la fuerza del propulsor de una combustión que comienza en el tiempo y termina en $t$ $1$ como ${\estilo de visualización t_{0}\,}$

Cambiando la variable de integración del tiempo $t$ a la masa de la nave espacial $m$ se obtiene

Suponiendo que sea una constante que no dependa de la cantidad de combustible restante, esta relación se integra a $v_{\text{exh}}\,$

cual es la ecuación del cohete de Tsiolkovsky .

Si, por ejemplo, el 20% de la masa de lanzamiento es combustible, lo que da una constante de 2100 m/s (un valor típico para un propulsor de hidracina ), la capacidad del sistema de control de reacción es $v_{\text{exh}}$ $\Delta {v}=2100\ \ln \left({\frac {1}{0.8}}\right)\,{\text{m/s}}=460\,{\text{m/s}}.$

Si es una función no constante de la cantidad de combustible restante ^[2] la capacidad del sistema de control de reacción se calcula mediante la integral ( 5 ). $v_{\text{exh}}$ $v_{\text{exh}}=v_{\text{exh}}(m)$

La aceleración ( 2 ) causada por la fuerza del propulsor es simplemente una aceleración adicional que se suma a las otras aceleraciones (fuerza por unidad de masa) que afectan a la nave espacial y la órbita se puede propagar fácilmente con un algoritmo numérico que también incluya esta fuerza del propulsor. ^[3] Pero para muchos propósitos, típicamente para estudios o para la optimización de maniobras, se aproximan mediante maniobras impulsivas como se ilustra en la figura 1 con un como se da por ( 4 ). De esta manera, se puede utilizar, por ejemplo, un enfoque de "cónicas parcheadas" que modele la maniobra como un cambio de una órbita de Kepler a otra mediante un cambio instantáneo del vector de velocidad. $\Delta {v}$

Esta aproximación con maniobras impulsivas es en la mayoría de los casos muy precisa, al menos cuando se utiliza propulsión química. Para sistemas de bajo empuje, típicamente sistemas de propulsión eléctrica , esta aproximación es menos precisa. Pero incluso para naves espaciales geoestacionarias que utilizan propulsión eléctrica para control fuera del plano con períodos de encendido de los propulsores que se extienden a lo largo de varias horas alrededor de los nodos, esta aproximación es aceptable.

Producción

El delta -v se genera normalmente mediante el empuje de un motor de cohete , pero puede generarse mediante otros motores. La tasa de cambio de delta- v en función del tiempo es la magnitud de la aceleración causada por los motores , es decir, el empuje por masa total del vehículo. El vector de aceleración real se hallaría sumando el empuje por masa al vector de gravedad y los vectores que representan cualquier otra fuerza que actúe sobre el objeto.

El delta- v total necesario es un buen punto de partida para las primeras decisiones de diseño, ya que la consideración de las complejidades agregadas se pospone para momentos posteriores en el proceso de diseño.

La ecuación del cohete muestra que la cantidad necesaria de combustible aumenta drásticamente con el aumento del delta -v . Por lo tanto, en los sistemas de propulsión de naves espaciales modernas se dedican estudios considerables a reducir el delta- v total necesario para un vuelo espacial determinado, así como a diseñar naves espaciales que sean capaces de producir delta- v mayores .

El aumento del delta- v proporcionado por un sistema de propulsión se puede lograr mediante:

puesta en escena
aumento del impulso específico
Mejora de la fracción de masa del propulsor

Maniobras múltiples

Debido a que las relaciones de masa se aplican a cualquier quemadura dada, cuando se realizan múltiples maniobras en secuencia, las relaciones de masa se multiplican.

De esta manera se puede demostrar que, siempre que la velocidad de escape sea fija, esto significa que delta- v se puede sumar:

Cuando $m 1, m 2$ son las relaciones de masas de las maniobras, y $v 1, v 2$ son los delta- v de la primera y segunda maniobras donde $V$ $=$ $v$ $1$ $+$ $v$ $2$ y $M$ $=$ $m$ $1$ $m$ $2$ . Esta es simplemente la ecuación del cohete aplicada a la suma de las dos maniobras. ${\begin{aligned}m_{1}m_{2}&=e^{V_{1}/V_{e}}e^{V_{2}/V_{e}}\\&=e^{\frac {V_{1}+V_{2}}{V_{e}}}\\&=e^{V/V_{e}}=M\end{aligned}}$

Esto es conveniente porque significa que se puede calcular delta- v y simplemente sumar y calcular la relación de masas solo para el vehículo en general para toda la misión. Por lo tanto, se suele citar delta- v en lugar de relaciones de masas que requerirían multiplicación.

Delta-enpresupuestos

Mapa delta -v de cuerpos seleccionados en el sistema solar, asumiendo que las quemaduras están en el periapsis y se ignoran la asistencia gravitatoria y los cambios de inclinación

Al diseñar una trayectoria, el presupuesto delta -v se utiliza como un buen indicador de cuánto combustible se necesitará. El uso de combustible es una función exponencial de delta- v de acuerdo con la ecuación del cohete ; también dependerá de la velocidad de escape.

No es posible determinar los requisitos de delta- v a partir de la conservación de la energía considerando solo la energía total del vehículo en las órbitas inicial y final, ya que la energía se elimina en el escape (ver también a continuación). Por ejemplo, la mayoría de las naves espaciales se lanzan en una órbita con una inclinación bastante cercana a la latitud en el sitio de lanzamiento, para aprovechar la velocidad de rotación de la superficie de la Tierra. Si es necesario, por razones relacionadas con la misión, colocar la nave espacial en una órbita de diferente inclinación , se requiere un delta- v sustancial, aunque las energías cinéticas y potenciales específicas en la órbita final y la órbita inicial sean iguales.

Cuando el empuje del cohete se aplica en ráfagas cortas, las otras fuentes de aceleración pueden ser despreciables, y la magnitud del cambio de velocidad de una ráfaga puede ser simplemente aproximada por el delta- v . El delta- v total a ser aplicado puede entonces simplemente encontrarse mediante la suma de cada uno de los delta- v's necesarios en los encendidos discretos, aun cuando entre ráfagas la magnitud y dirección de la velocidad cambie debido a la gravedad, por ejemplo en una órbita elíptica .

Para ver ejemplos de cálculo de delta- v , véase la órbita de transferencia de Hohmann , la honda gravitacional y la red de transporte interplanetario . También es de destacar que un gran empuje puede reducir la resistencia gravitatoria .

El delta- v también es necesario para mantener los satélites en órbita y se gasta en maniobras de mantenimiento de la posición orbital . Dado que la carga de combustible de la mayoría de los satélites no se puede reponer, la cantidad de combustible cargado inicialmente en un satélite puede determinar su vida útil.

Efecto Oberth

A partir de consideraciones de potencia, resulta que al aplicar delta- v en la dirección de la velocidad, la energía orbital específica ganada por unidad de delta -v es igual a la velocidad instantánea. Esto se denomina efecto Oberth.

Por ejemplo, un satélite en una órbita elíptica se impulsa de manera más eficiente a alta velocidad (es decir, a pequeña altitud) que a baja velocidad (es decir, a gran altitud).

Otro ejemplo es que cuando un vehículo pasa por un planeta, quemar el propulsor en el punto de máxima aproximación en lugar de más lejos proporciona una velocidad final significativamente mayor, y esto es aún más así cuando el planeta es grande y tiene un campo gravitatorio profundo, como Júpiter.

Parcela de chuletas de cerdo

Debido a que las posiciones relativas de los planetas cambian con el tiempo, se requieren diferentes delta-v en diferentes fechas de lanzamiento. Un diagrama que muestra el delta- v requerido graficado en función del tiempo a veces se denomina diagrama de chuleta de cerdo . Este tipo de diagrama es útil porque permite calcular una ventana de lanzamiento , ya que el lanzamiento solo debería ocurrir cuando la misión esté dentro de las capacidades del vehículo que se va a utilizar. ^[4]

Alrededor del sistema solar

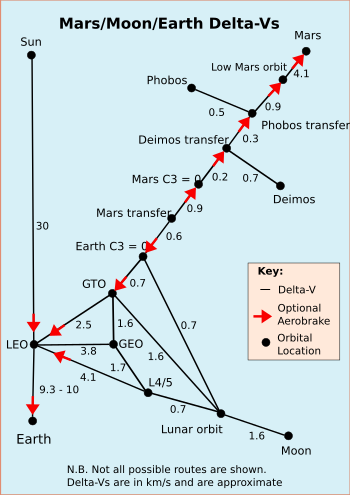
Delta- v necesario para varias maniobras orbitales que utilizan cohetes convencionales; las flechas rojas muestran dónde se puede realizar un frenado aerodinámico opcional en esa dirección particular, los números negros dan delta- v en km/s que se aplican en cualquier dirección. ^[5]^{[6] A menudo se pueden lograr transferencias de delta}-v menores que las mostradas, pero involucran ventanas de transferencia raras o toman significativamente más tiempo, ver: Mecánica orbital § Red de transporte interplanetario y órbitas difusas .

C3: Órbita de escape
GEO: Órbita geoestacionaria
GTO: Órbita de transferencia geoestacionaria
L4/5: Punto Lagrangiano Tierra-Luna L 4 L 5
LEÓN: Órbita terrestre baja

Reentrada en órbita terrestre baja

Por ejemplo, la nave espacial Soyuz sale de la órbita de la ISS en dos pasos. Primero, necesita una velocidad delta- v de 2,18 m/s para separarse de forma segura de la estación espacial. Luego, necesita otros 128 m/s para volver a entrar . ^[7]

Véase también

Referencias

^ Sarigul-Klijn, Nesrin; Noël, Chris; Sarigul-Klijn, Martinus (5 de enero de 2004). Lanzamiento aéreo de vehículos Tierra a Órbita: Delta V se beneficia de las condiciones de lanzamiento y la aerodinámica del vehículo. doi :10.2514/6.2004-872. ISBN 9781624100789.
^ Puede ser el caso de un sistema de "purga" en el cual la presión en el tanque disminuye cuando se ha usado combustible y no solo disminuye el caudal de combustible sino también, en menor medida, la velocidad de escape . $\rho$ $v_{\text{exh}}$
^ La fuerza de empuje por unidad de masa es donde y son funciones dadas del tiempo . ${\frac {f(t)}{m(t)}}=v_{\text{exh}}(t){\frac {{\dot {m}}(t)}{m(t)}}$ $f(t)$ $m(t)$ $t$
^ "Exploración de Marte: características". marsprogram.jpl.nasa.gov .
^ "Cohetes y transporte espacial". Archivado desde el original el 1 de julio de 2007. Consultado el 1 de junio de 2013 .
^ "Calculadora Delta-V". Archivado desde el original el 12 de marzo de 2000.Proporciona cifras de 8,6 desde la superficie de la Tierra hasta la órbita baja terrestre (LEO), 4,1 y 3,8 desde la LEO hasta la órbita lunar (o L5) y GEO respectivamente, 0,7 desde L5 hasta la órbita lunar y 2,2 desde la órbita lunar hasta la superficie lunar. Se dice que las cifras proceden del Capítulo 2 de Space Settlements: A Design Study, archivado el 28 de noviembre de 2001 en los Archivos web de la Biblioteca del Congreso en el sitio web de la NASA ^{[ enlace muerto ‍ ]} .
^ Gebhardt, Chris (17 de abril de 2021). «La Soyuz MS-17 devuelve de forma segura a tres miembros de la tripulación de la Estación a Kazajstán». nasaspaceflight.com . Consultado el 10 de julio de 2022 .