En geometría sólida , una cuña es un poliedro definido por dos triángulos y tres caras trapezoidales . Una cuña tiene cinco caras, nueve aristas y seis vértices.
Una cuña es un poliedro de base rectangular, cuyas caras son dos triángulos isósceles y dos trapecios que se encuentran en la parte superior de una arista. [1] . Un prismatoide se define como un poliedro donde sus vértices se encuentran en dos planos paralelos, con sus caras laterales son triángulos, trapecios y paralelogramos ; [2] la cuña es un ejemplo de prismatoide porque su arista superior es paralela a la base rectangular. [3] El volumen de una cuña es donde el rectángulo de la base es por , es la longitud de la arista del vértice paralela a , y es la altura desde el rectángulo de la base hasta la arista del vértice. [1]
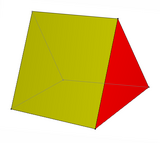
En algunos casos especiales, la cuña es el prisma recto si todos los bordes que conectan triángulos tienen la misma longitud y las caras triangulares son perpendiculares a la base rectangular. [3]
Las cuñas se pueden crear a partir de la descomposición de otros poliedros. Por ejemplo, el dodecaedro se puede dividir en un cubo central con 6 cuñas que cubren las caras del cubo. Las orientaciones de las cuñas son tales que las caras del triángulo y del trapezoide se pueden conectar y formar un pentágono regular .
Se pueden formar dos cuñas obtusas dividiendo por la mitad un tetraedro regular en un plano paralelo a dos bordes opuestos.