Teorema de Kirchhoff

Sobre el número de árboles de expansión en un gráfico

En el campo matemático de la teoría de grafos , el teorema de Kirchhoff o teorema del árbol matricial de Kirchhoff, llamado así por Gustav Kirchhoff, es un teorema sobre el número de árboles de expansión en un grafo , que muestra que este número se puede calcular en tiempo polinomial a partir del determinante de una submatriz de la matriz laplaciana del grafo ; específicamente, el número es igual a cualquier cofactor de la matriz laplaciana. El teorema de Kirchhoff es una generalización de la fórmula de Cayley que proporciona el número de árboles de expansión en un grafo completo .

El teorema de Kirchhoff se basa en la noción de matriz laplaciana de un grafo, que es igual a la diferencia entre la matriz de grados del grafo (la matriz diagonal de grados de los vértices ) y su matriz de adyacencia (una matriz (0,1) con 1 en los lugares correspondientes a las entradas donde los vértices son adyacentes y 0 en caso contrario).

Para un grafo conexo G dado con n vértices etiquetados , sean λ ₁ ,  λ ₂ , ...,  λ _{n −1 los} valores propios no nulos de su matriz laplaciana. Entonces, el número de árboles de expansión de G es

${\displaystyle t(G)={\frac {1}{n}}\lambda _{1}\lambda _{2}\cdots \lambda _{n-1}\,.}$

JB O'Toole realizó una traducción al inglés del artículo original de Kirchhoff de 1847 y la publicó en 1958. ^[1]

Un ejemplo que utiliza el teorema del árbol de matrices

El teorema del árbol matricial se puede utilizar para calcular el número de árboles de expansión etiquetados de este gráfico.

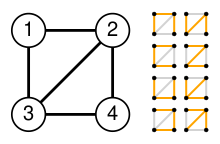
Primero, construya la matriz laplaciana Q para el gráfico de diamante de ejemplo G (ver imagen a la derecha):

${\displaystyle Q=\left[{\begin{array}{rrrr}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{array}}\right].}$

A continuación, construya una matriz Q ^* eliminando cualquier fila y cualquier columna de Q. Por ejemplo, eliminar la fila 1 y la columna 1 da como resultado

${\displaystyle Q^{\ast }=\left[{\begin{array}{rrr}3&-1&-1\\-1&3&-1\\-1&-1&2\end{array}}\right].}$

Finalmente, tome el determinante de Q ^* para obtener t ( G ), que es 8 para el gráfico de diamante. (Observe que t ( G ) es el cofactor (1,1) de Q en este ejemplo).

Esquema de prueba

(La prueba a continuación se basa en la fórmula de Cauchy-Binet . Un argumento de inducción elemental para el teorema de Kirchhoff se puede encontrar en la página 654 de Moore (2011). ^[2] )

En primer lugar, observe que la matriz laplaciana tiene la propiedad de que la suma de sus elementos en cualquier fila y cualquier columna es 0. Por lo tanto, podemos transformar cualquier matriz menor en cualquier otra matriz menor sumando filas y columnas, intercambiándolas y multiplicando una fila o una columna por −1. Por lo tanto, los cofactores son los mismos hasta el signo y se puede verificar que, de hecho, tienen el mismo signo.

Procedemos a demostrar que el determinante del menor M ₁₁ cuenta el número de árboles de expansión. Sea n el número de vértices del grafo y m el número de sus aristas. La matriz de incidencia E es una matriz n por m , que puede definirse de la siguiente manera: supongamos que ( i , j ) es la arista k del grafo y que i < j . Entonces E _ik = 1, E _jk = −1 y todas las demás entradas en la columna k son 0 (véase la matriz de incidencia orientada para comprender esta matriz de incidencia modificada E ). Para el ejemplo anterior (con n = 4 y m = 5):

${\displaystyle E={\begin{bmatrix}1&1&0&0&0\\-1&0&1&1&0\\0&-1&-1&0&1\\0&0&0&-1&-1\\\end{bmatrix}}.}$

Recordemos que el laplaciano L se puede factorizar en el producto de la matriz de incidencia y su transpuesta , es decir, L = EE ^T . Además, sea F la matriz E con su primera fila eliminada, de modo que FF ^T = M ₁₁ .

Ahora la fórmula de Cauchy-Binet nos permite escribir

${\displaystyle \det \left(M_{11}\right)=\sum _{S}\det \left(F_{S}\right)\det \left(F_{S}^{\mathrm {T} }\right)=\sum _{S}\det \left(F_{S}\right)^{2}}$

donde S abarca subconjuntos de [ m ] de tamaño n − 1, y F _S denota la matriz ( n − 1)-por-( n − 1) cuyas columnas son las de F con índice en S . Entonces cada S especifica n − 1 aristas del grafo original, y se puede demostrar que esas aristas inducen un árbol de expansión si y solo si el determinante de F _S es +1 o −1, y que no inducen un árbol de expansión si y solo si el determinante es 0. Esto completa la prueba.

Casos particulares y generalizaciones

La fórmula de Cayley

La fórmula de Cayley se desprende del teorema de Kirchhoff como un caso especial, ya que cada vector con 1 en un lugar, −1 en otro lugar y 0 en el resto es un vector propio de la matriz laplaciana del grafo completo, siendo el valor propio correspondiente n . Estos vectores juntos abarcan un espacio de dimensión n  − 1, por lo que no hay otros valores propios distintos de cero.

Como alternativa, tenga en cuenta que, como la fórmula de Cayley cuenta la cantidad de árboles etiquetados distintos de un gráfico completo K _{n ,} necesitamos calcular cualquier cofactor de la matriz laplaciana de K _n . La matriz laplaciana en este caso es

${\displaystyle {\begin{bmatrix}n-1&-1&\cdots &-1\\-1&n-1&\cdots &-1\\\vdots &\vdots &\ddots &\vdots \\-1&-1&\cdots &n-1\\\end{bmatrix}}.}$

Cualquier cofactor de la matriz anterior es n ^{n −2} , que es la fórmula de Cayley.

Teorema de Kirchhoff para multigrafos

El teorema de Kirchhoff también es válido para multigrafos ; la matriz Q se modifica de la siguiente manera:

• La entrada q _i,j es igual a − m , donde m es el número de aristas entre i y j ;
• Al contar el grado de un vértice, se excluyen todos los bucles .

La fórmula de Cayley para un multigrafo completo es m ^{n −1} ( n ^{n −1} −( n −1) n ^{n −2} ) mediante los mismos métodos producidos anteriormente, ya que un grafo simple es un multigrafo con m = 1.

Enumeración explícita de árboles de expansión

El teorema de Kirchhoff se puede reforzar modificando la definición de la matriz laplaciana. En lugar de simplemente contar las aristas que emanan de cada vértice o que conectan un par de vértices, etiquete cada arista con una indeterminación y deje que la entrada ( i , j )-ésima de la matriz laplaciana modificada sea la suma sobre las indeterminaciones correspondientes a las aristas entre los vértices i -ésimo y j -ésimo cuando i no es igual a j , y la suma negativa sobre todas las indeterminaciones correspondientes a las aristas que emanan del vértice i -ésimo cuando i es igual a j .

El determinante de la matriz laplaciana modificada, obtenida eliminando cualquier fila y columna (de forma similar a encontrar el número de árboles de expansión de la matriz laplaciana original), es entonces un polinomio homogéneo (el polinomio de Kirchhoff) en las indeterminadas correspondientes a las aristas del grafo. Después de recopilar los términos y realizar todas las cancelaciones posibles, cada monomio en la expresión resultante representa un árbol de expansión que consiste en las aristas correspondientes a las indeterminadas que aparecen en ese monomio. De esta manera, se puede obtener una enumeración explícita de todos los árboles de expansión del grafo simplemente calculando el determinante.

Para una demostración de esta versión del teorema véase Bollobás (1998). ^[3]

Matroides

Los árboles de expansión de un grafo forman las bases de un matroide gráfico , por lo que el teorema de Kirchhoff proporciona una fórmula para contar el número de bases en un matroide gráfico. El mismo método también se puede utilizar para contar el número de bases en matroides regulares , una generalización de los matroides gráficos (Maurer 1976).

Teorema de Kirchhoff para multigrafos dirigidos

El teorema de Kirchhoff se puede modificar para contar la cantidad de árboles de expansión orientados en multigrafos dirigidos. La matriz Q se construye de la siguiente manera:

• La entrada q _i,j para i y j distintos es igual a − m , donde m es el número de aristas de i a j ;
• La entrada q _i,i es igual al grado de entrada de i menos el número de bucles en i .

El número de árboles de expansión orientados con raíz en un vértice i es el determinante de la matriz obtenida al eliminar la i- ésima fila y columna de Q

Contando abarcandoa-bosques componentes

El teorema de Kirchhoff se puede generalizar para contar bosques de expansión de k componentes en un grafo no ponderado. ^[4] Un bosque de expansión de k componentes es un subgrafo con k componentes conectados que contiene todos los vértices y no tiene ciclos, es decir, hay como máximo un camino entre cada par de vértices. Dado un bosque F con componentes conectados , defina su peso como el producto del número de vértices en cada componente. Entonces ${\textstyle F_{1},\dots ,F_{k}}$ ${\textstyle w(F)=|V(F_{1})|\cdot \dots \cdot |V(F_{k})|}$

${\displaystyle \sum _{F}w(F)=q_{k},}$

donde la suma es sobre todos los bosques que abarcan k componentes y es el coeficiente del polinomio ${\textstyle q_{k}}$ ${\textstyle x^{k}}$

${\displaystyle (x+\lambda _{1})\dots (x+\lambda _{n-1})x.}$

El último factor del polinomio se debe al valor propio cero . Más explícitamente, el número se puede calcular como ${\textstyle \lambda _{n}=0}$ ${\textstyle q_{k}}$

${\displaystyle q_{k}=\sum _{\{i_{1},\dots ,i_{n-k}\}\subset \{1\dots n-1\}}\lambda _{i_{1}}\dots \lambda _{i_{n-k}}.}$

donde la suma es sobre todos los subconjuntos de n − k elementos de . Por ejemplo ${\textstyle \{1,\dots ,n\}}$

${\displaystyle {\begin{aligned}q_{n-1}&=\lambda _{1}+\dots +\lambda _{n-1}=\mathrm {tr} Q=2|E|\\q_{n-2}&=\lambda _{1}\lambda _{2}+\lambda _{1}\lambda _{3}+\dots +\lambda _{n-2}\lambda _{n-1}\\q_{2}&=\lambda _{1}\dots \lambda _{n-2}+\lambda _{1}\dots \lambda _{n-3}\lambda _{n-1}+\dots +\lambda _{2}\dots \lambda _{n-1}\\q_{1}&=\lambda _{1}\dots \lambda _{n-1}\\\end{aligned}}}$

Dado que un bosque de expansión con n −1 componentes corresponde a una única arista, el caso k = n −1 establece que la suma de los valores propios de Q es el doble del número de aristas. El caso k = 1 corresponde al teorema de Kirchhoff original, ya que el peso de cada árbol de expansión es n .

La demostración puede realizarse de forma análoga a la del teorema de Kirchhoff. Una submatriz invertible de la matriz de incidencia corresponde biyectivamente a un bosque de k componentes con una elección de vértice para cada componente. ${\displaystyle (n-k)\times (n-k)}$

Los coeficientes son hasta el signo de los coeficientes del polinomio característico de Q. ${\textstyle q_{k}}$

Véase también

• Lista de temas relacionados con los árboles
• Teorema BEST
• Teorema del árbol de cadenas de Markov
• Árbol de expansión mínimo
• Secuencia de Prüfer

Referencias

1. O'Toole, JB "Sobre la solución de las ecuaciones obtenidas a partir de la investigación de la distribución lineal de corrientes galvánicas". IRE Transactions on Circuit Theory . 5 (1): 4–7. doi :10.1109/TCT.1958.1086426.
2. Moore, Cristopher (2011). La naturaleza de la computación . Oxford, Inglaterra, Nueva York: Oxford University Press. ISBN 978-0-19-923321-2.OCLC 180753706  .
3. Bollobás, Béla (1998). Teoría de grafos moderna . Nueva York: Springer. doi :10.1007/978-1-4612-0619-4. ISBN 978-0-387-98488-9.
4. Biggs, N. (1993). Teoría de grafos algebraicos . Cambridge University Press.

• Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael J. (2008), Combinatoria y teoría de grafos , Textos de pregrado en matemáticas (2.ª ed.), Springer.
• Maurer, Stephen B. (1976), "Generalizaciones matriciales de algunos teoremas sobre árboles, ciclos y cociclos en grafos", SIAM Journal on Applied Mathematics , 30 (1): 143–148, doi :10.1137/0130017, MR  0392635.
• Tutte, WT (2001), Teoría de grafos , Cambridge University Press, pág. 138, ISBN 978-0-521-79489-3.
• Chaiken, S.; Kleitman, D. (1978), "Teoremas del árbol matricial", Journal of Combinatorial Theory, Serie A , 24 (3): 377–381, doi : 10.1016/0097-3165(78)90067-5 , ISSN  0097-3165

Enlaces externos

• Una demostración del teorema de Kirchhoff