Muestreo de rebanadas

Algoritmo

El muestreo de sectores es un tipo de algoritmo Monte Carlo de cadena de Markov para muestreo de números pseudoaleatorios , es decir, para extraer muestras aleatorias de una distribución estadística. El método se basa en la observación de que para muestrear una variable aleatoria se puede muestrear uniformemente de la región bajo la gráfica de su función de densidad. ^{[1] [2] [3]}

Motivación

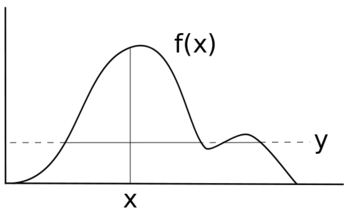
Supongamos que desea muestrear alguna variable aleatoria X con distribución f ( x ). Supongamos que la siguiente es la gráfica de f ( x ). La altura de f ( x ) corresponde a la probabilidad en ese punto.

Si tomara una muestra uniforme de X , cada valor tendría la misma probabilidad de ser muestreado y su distribución sería de la forma f ( x ) = y para algún valor de y en lugar de alguna función no uniforme f ( x ). En lugar de la línea negra original, su nueva distribución se parecería más a la línea azul.

Para muestrear X de una manera que retenga la distribución f ( x ), se debe utilizar alguna técnica de muestreo que tenga en cuenta las distintas probabilidades para cada rango de f ( x ).

Método

El muestreo por cortes, en su forma más simple, toma muestras uniformemente desde debajo de la curva f ( x ) sin la necesidad de rechazar ningún punto, de la siguiente manera:

1. Elija un valor inicial x ₀ para el cual f ( x ₀ ) > 0.
2. Muestra un valor de y uniformemente entre 0 y f ( x ₀ ).
3. Dibuja una línea horizontal a través de la curva en esta posición y .
4. Muestre un punto ( x , y ) de los segmentos de línea dentro de la curva.
5. Repita desde el paso 2 usando el nuevo valor de x .

La motivación aquí es que una forma de muestrear un punto uniformemente desde dentro de una curva arbitraria es dibujar primero cortes horizontales delgados de altura uniforme a lo largo de toda la curva. Luego, podemos muestrear un punto dentro de la curva seleccionando aleatoriamente un segmento que cae en o debajo de la curva en la posición x de la iteración anterior, y luego seleccionando aleatoriamente una posición x en algún lugar a lo largo del segmento. Al utilizar la posición x de la iteración anterior del algoritmo, a largo plazo seleccionamos sectores con probabilidades proporcionales a las longitudes de sus segmentos dentro de la curva. La parte más difícil de este algoritmo es encontrar los límites del corte horizontal, lo que implica invertir la función que describe la distribución de la que se está muestreando. Esto es especialmente problemático para distribuciones multimodales, donde el segmento puede constar de múltiples partes discontinuas. A menudo es posible utilizar una forma de muestreo de rechazo para superar esto, donde tomamos muestras de un segmento más grande que se sabe que incluye el segmento deseado en cuestión y luego descartamos puntos fuera del segmento deseado. Este algoritmo se puede utilizar para tomar muestras del área bajo cualquier curva, independientemente de si la función se integra a 1. De hecho, escalar una función mediante una constante no tiene ningún efecto en las posiciones x muestreadas. Esto significa que el algoritmo se puede utilizar para tomar muestras de una distribución cuya función de densidad de probabilidad solo se conoce hasta una constante (es decir, cuya constante de normalización se desconoce), lo cual es común en estadística computacional .

Implementación

El muestreo de sectores recibe su nombre del primer paso: definir un sector mediante muestreo a partir de una variable auxiliar . Esta variable se toma como muestra de , donde es la función de densidad de probabilidad (PDF) de X o es al menos proporcional a su PDF. Esto define una porción de X donde . En otras palabras, ahora estamos mirando una región de X donde la densidad de probabilidad es al menos . Luego, el siguiente valor de X se muestrea uniformemente de este segmento. Se muestra un nuevo valor de , luego X , y así sucesivamente. Esto se puede visualizar como un muestreo alternativo de la posición y y luego de la posición x de los puntos en PDF, por lo que las X provienen de la distribución deseada. Los valores no tienen consecuencias o interpretaciones particulares fuera de su utilidad para el procedimiento. ${\displaystyle Y}$ ${\displaystyle [0,f(x)]}$ ${\displaystyle f(x)}$ ${\displaystyle f(x)\geq Y}$ ${\displaystyle Y}$ ${\displaystyle Y}$ ${\displaystyle Y}$

Si tanto la PDF como su inversa están disponibles, y la distribución es unimodal, entonces encontrar la porción y tomar muestras de ella es simple. De lo contrario, se puede utilizar un procedimiento de salida para encontrar una región cuyos puntos finales queden fuera del segmento. Luego, se puede extraer una muestra del corte mediante muestreo de rechazo . Radford M. Neal describe en detalle varios procedimientos para esto . ^[2]

Tenga en cuenta que, a diferencia de muchos métodos disponibles para generar números aleatorios a partir de distribuciones no uniformes, las variables aleatorias generadas directamente por este enfoque exhibirán una dependencia estadística en serie. Esto se debe a que para extraer la siguiente muestra, definimos el sector en función del valor de f ( x ) para la muestra actual.

Comparado con otros métodos

El muestreo de cortes es un método de cadena de Markov y, como tal, tiene el mismo propósito que el muestreo de Gibbs y Metropolis. A diferencia de Metropolis, no es necesario ajustar manualmente la función candidata o la desviación estándar candidata.

Recuerde que Metropolis es sensible al tamaño del paso. Si el tamaño del paso es demasiado pequeño, la caminata aleatoria provoca una descorrelación lenta. Si el tamaño del paso es demasiado grande, se produce una gran ineficiencia debido a una alta tasa de rechazo.

A diferencia de Metropolis, el muestreo de sectores ajusta automáticamente el tamaño del paso para que coincida con la forma local de la función de densidad. Podría decirse que la implementación es más fácil y eficiente que el muestreo de Gibbs o las simples actualizaciones de Metropolis.

Tenga en cuenta que, a diferencia de muchos métodos disponibles para generar números aleatorios a partir de distribuciones no uniformes, las variables aleatorias generadas directamente por este enfoque exhibirán una dependencia estadística en serie. En otras palabras, no todos los puntos tienen la misma probabilidad independiente de selección. Esto se debe a que para extraer la siguiente muestra, definimos el sector en función del valor de f(x) para la muestra actual. Sin embargo, las muestras generadas son markovianas y, por lo tanto, se espera que converjan a la distribución correcta a largo plazo.

Slice Sampling requiere que la distribución que se va a muestrear sea evaluable. Una forma de relajar este requisito es sustituir una distribución evaluable que sea proporcional a la distribución verdadera no evaluable.

Caso univariado

Para una muestra x dada, se elige un valor para y entre [0, f ( x )], que define una "porción" de la distribución (mostrada por la línea horizontal continua). En este caso, hay dos sectores separados por un área fuera del rango de la distribución.

Para muestrear una variable aleatoria X con densidad f ( x ), introducimos una variable auxiliar Y e iteramos de la siguiente manera:

• Dada una muestra x elegimos y uniformemente al azar del intervalo [0, f ( x )];
• dado y elegimos x uniformemente al azar del conjunto . ${\displaystyle f^{-1}[y,+\infty )}$
• La muestra de x se obtiene ignorando los valores de y .

Nuestra variable auxiliar Y representa una "porción" horizontal de la distribución. El resto de cada iteración se dedica a muestrear un valor de x del segmento que sea representativo de la densidad de la región que se está considerando.

En la práctica, el muestreo de una porción horizontal de una distribución multimodal es difícil. Existe una tensión entre obtener una región de muestreo grande y, por lo tanto, hacer posibles grandes movimientos en el espacio de distribución, y obtener una región de muestreo más simple para aumentar la eficiencia. Una opción para simplificar este proceso es la expansión y contracción regional.

• Primero, se utiliza un parámetro de ancho w para definir el área que contiene el valor 'x dado. Cada punto final de esta área se prueba para ver si se encuentra fuera del segmento dado. De lo contrario, la región se extiende en la(s) dirección(es) apropiada(s) mediante w hasta que ambos puntos finales queden fuera del corte.
• Se selecciona una muestra candidata uniformemente dentro de esta región. Si la muestra candidata se encuentra dentro del segmento, se acepta como nueva muestra. Si se encuentra fuera del sector, el punto candidato se convierte en el nuevo límite de la región. Se toma una nueva muestra candidata de manera uniforme. El proceso se repite hasta que la muestra candidata esté dentro del segmento. (Consulte el diagrama para ver un ejemplo visual).

Encontrar una muestra dado un conjunto de cortes (los cortes se representan aquí como líneas azules y corresponden a los cortes de línea continua en el gráfico anterior de f ( x )). a) Se establece un parámetro de ancho w . b) Alrededor de un punto dado se identifica una región de ancho w . c) La región se expande en w hasta que ambos puntos finales estén fuera del segmento considerado. d) se selecciona uniformemente de la región. e) Dado que se encuentra fuera del segmento considerado, el límite izquierdo de la región se ajusta a . f) Se toma otra muestra uniforme y se acepta como muestra ya que se encuentra dentro de la porción considerada. ${\displaystyle x_{0}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{1}}$ ${\displaystyle x}$

→

Muestreo de corte dentro de Gibbs

En un muestreador de Gibbs , es necesario extraer de manera eficiente todas las distribuciones condicionales completas. Cuando el muestreo a partir de una densidad totalmente condicional no es fácil, se puede utilizar una sola iteración de muestreo por cortes o el algoritmo Metropolis-Hastings dentro de Gibbs para tomar muestras de la variable en cuestión. Si la densidad totalmente condicional es log-cóncava, una alternativa más eficiente es la aplicación de métodos de muestreo de rechazo adaptativo (ARS). ^{[4] [5]} Cuando no se pueden aplicar las técnicas ARS (dado que el condicional completo no es logcóncavo), a menudo se emplean los algoritmos de muestreo de Metropolis de rechazo adaptativo . ^{[6] [7]}

Métodos multivariados

Tratar cada variable de forma independiente

El muestreo de corte de una sola variable se puede utilizar en el caso multivariado muestreando cada variable repetidamente, como en el muestreo de Gibbs. Para hacerlo es necesario que podamos calcular, para cada componente, una función que sea proporcional a . ${\displaystyle x_{i}}$ ${\displaystyle p(x_{i}|x_{0}...x_{n})}$

Para evitar el comportamiento de caminata aleatoria, se pueden utilizar métodos de relajación excesiva para actualizar cada variable por turno. ^{[ cita necesaria ]} La relajación excesiva elige un nuevo valor en el lado opuesto de la moda del valor actual, en lugar de elegir un nuevo valor independiente de la distribución como se hace en Gibbs.

Muestreo de cortes de hiperrectángulo

Este método adapta el algoritmo univariado al caso multivariado sustituyendo la región w unidimensional utilizada en el original por un hiperrectángulo. El hiperrectángulo H se inicializa en una posición aleatoria sobre el corte. Luego, H se reduce a medida que se rechazan puntos.

Muestreo de corte reflectante

El muestreo de corte reflectante es una técnica para suprimir el comportamiento de caminata aleatoria en la que las sucesivas muestras candidatas de distribución f ( x ) se mantienen dentro de los límites del corte "reflejando" la dirección del muestreo hacia el interior del corte una vez que se ha alcanzado el límite.

En esta representación gráfica del muestreo reflexivo, la forma indica los límites de un segmento de muestreo. Los puntos indican los puntos de inicio y finalización de una caminata de muestreo. Cuando las muestras alcanzan los límites del segmento, la dirección del muestreo se "refleja" nuevamente en el segmento.

Ejemplo

Considere un ejemplo de una sola variable. Supongamos que nuestra distribución verdadera es una distribución normal con media 0 y desviación estándar 3 ,. Entonces: . El pico de la distribución es obviamente en ese punto . ${\displaystyle g(x)\sim N(0,3^{2})}$ ${\displaystyle f(x)={\frac {1}{\sqrt {2\pi \cdot 3^{2}}}}\ e^{-{\frac {(x-0)^{2}}{2\cdot 3^{2}}}}}$ ${\displaystyle x=0}$ ${\displaystyle f(x)\approx 0.1330}$

1. Primero extraemos un valor aleatorio uniforme y del rango de f ( x ) para definir nuestra(s) porción(es). f ( x ) varía de 0 a ~0,1330, por lo que cualquier valor entre estos dos extremos es suficiente. Supongamos que tomamos y = 0,1. El problema es cómo muestrear puntos que tienen valores y > 0,1.
2. A continuación, configuramos nuestro parámetro de ancho w que usaremos para expandir nuestra región de consideración. Este valor es arbitrario. Supongamos w = 2.
3. A continuación, necesitamos un valor inicial para x . Dibujamos x de la distribución uniforme dentro del dominio de f ( x ) que satisface f ( x ) > 0,1 (nuestro parámetro y ). Supongamos que x = 2. Esto funciona porque f (2) = ~0,1065 > 0,1. ^[8]
4. Como x = 2 y w = 2, nuestra región de interés actual está limitada por (1, 3).
5. Ahora, se prueba cada punto final de esta área para ver si se encuentra fuera del segmento dado. Nuestro límite derecho se encuentra fuera de nuestro segmento ( f (3) = ~0.0807 < 0.1), pero el valor izquierdo no ( f (1) = ~0.1258 > 0.1). Ampliamos el límite izquierdo agregándole w hasta que se extienda más allá del límite del corte. Después de este proceso, los nuevos límites de nuestra región de interés son (−3, 3).
6. A continuación, tomamos una muestra uniforme dentro de (−3, 3). Supongamos que esta muestra produce x = −2,9. Aunque esta muestra está dentro de nuestra región de interés, no se encuentra dentro de nuestra porción (f(2.9) = ~0.08334 < 0.1), por lo que modificamos el límite izquierdo de nuestra región de interés hasta este punto. Ahora tomamos una muestra uniforme de (−2,9, 3). Supongamos que esta vez nuestra muestra produce x = 1, que está dentro de nuestro segmento y, por lo tanto, es la salida de muestra aceptada mediante muestreo de segmento. Si nuestra nueva x no hubiera estado dentro de nuestro segmento, continuaríamos el proceso de reducción/remuestreo hasta que se encontrara una x válida dentro de los límites.

Si estamos interesados ​​en el pico de la distribución, podemos seguir repitiendo este proceso ya que el nuevo punto corresponde a una f ( x ) mayor que el punto original.

Otro ejemplo

Para tomar muestras de la distribución normal, primero elegimos una x inicial , digamos 0. Después de cada muestra de x, elegimos y uniformemente al azar de , que está acotada por la función de densidad de probabilidad de . Después de cada muestra y elegimos x uniformemente al azar de donde . Esta es la porción donde . ${\displaystyle N(0,1)}$ ${\displaystyle (0,e^{-x^{2}/2}/{\sqrt {2\pi }}]}$ ${\displaystyle N(0,1)}$ ${\displaystyle [-\alpha ,\alpha ]}$ ${\displaystyle \alpha ={\sqrt {-2\ln(y{\sqrt {2\pi }})}}}$ ${\displaystyle f(x)>y}$

Una implementación en el lenguaje Macsyma es:

rebanada ( x ) :=  bloque ([ y ,  alpha ] ,  y: aleatorio ( exp ( - x ^ 2  /  2.0 ) /  sqrt ( 2.0  *  dfloat ( % pi ))) ,  alpha: sqrt ( -2.0  *  ln ( y  *  sqrt ( 2.0  *  dfloat ( % pi )))) ,  x: signum ( aleatorio ()) *  aleatorio ( alfa )) ;

Ver también

• Cadena de Markov Montecarlo

Referencias

1. Damlen, P., Wakefield, J. y Walker, S. (1999). Muestreo de Gibbs para modelos bayesianos jerárquicos y no conjugados mediante el uso de variables auxiliares. Revista de la Royal Statistical Society, Serie B (Metodología estadística), 61(2), 331-344.Chicago
2. Neal, Radford M. (2003). "Muestreo de cortes". Anales de Estadística . 31 (3): 705–767. doi : 10.1214/aos/1056562461 . SEÑOR  1994729. Zbl  1051.65007.
3. Obispo, Christopher (2006). "11.4: Muestreo de sectores". Reconocimiento de patrones y aprendizaje automático . Saltador . ISBN 978-0387310732.
4. Gilks, WR; Salvaje, P. (1 de enero de 1992). "Muestreo de rechazo adaptativo para muestreo de Gibbs". Revista de la Real Sociedad de Estadística. Serie C (Estadística Aplicada) . 41 (2): 337–348. doi :10.2307/2347565. JSTOR  2347565.
5. Hörmann, Wolfgang (1 de junio de 1995). "Una técnica de rechazo para el muestreo de distribuciones cóncavas en T". Transmisión ACM. Matemáticas. Software . 21 (2): 182-193. CiteSeerX 10.1.1.56.6055 . doi :10.1145/203082.203089. ISSN  0098-3500. S2CID  592740. 
6. Gilks, WR; Mejor, NG ; Bronceado, KKC (1 de enero de 1995). "Muestreo de metrópolis de rechazo adaptativo dentro del muestreo de Gibbs". Revista de la Real Sociedad de Estadística. Serie C (Estadística Aplicada) . 44 (4): 455–472. doi :10.2307/2986138. JSTOR  2986138.
7. Meyer, Renate; Cai, Bo; Perron, François (15 de marzo de 2008). "Muestreo de Metropolis de rechazo adaptativo utilizando polinomios de interpolación de Lagrange de grado 2". Estadística computacional y análisis de datos . 52 (7): 3408–3423. doi : 10.1016/j.csda.2008.01.005.
8. Tenga en cuenta que si no sabemos cómo seleccionar x de manera que f ( x ) > y , aún podemos elegir cualquier valor aleatorio para x , evaluar f ( x ) y usarlo como nuestro valor de y . y solo inicializa el algoritmo; A medida que avanza el algoritmo, encontrará valores cada vez más altos de y .

enlaces externos

• http://www.probability.ca/jeff/java/slice.html