
El modelado de ecuaciones estructurales ( SEM ) es un conjunto diverso de métodos que utilizan los científicos que realizan investigaciones tanto observacionales como experimentales. El SEM se utiliza principalmente en las ciencias sociales y del comportamiento, pero también se utiliza en epidemiología, [2] negocios, [3] y otros campos. Una definición de SEM es difícil sin hacer referencia al lenguaje técnico, pero un buen punto de partida es el nombre en sí.
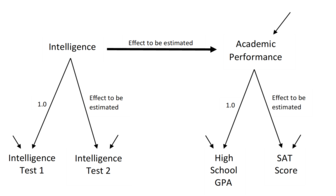
El modelo SEM implica un modelo que representa cómo se cree que varios aspectos de un fenómeno se conectan causalmente entre sí. Los modelos de ecuaciones estructurales a menudo contienen conexiones causales postuladas entre algunas variables latentes (variables que se cree que existen pero que no se pueden observar directamente). Las conexiones causales adicionales vinculan esas variables latentes con las variables observadas cuyos valores aparecen en un conjunto de datos. Las conexiones causales se representan mediante ecuaciones , pero la estructuración postulada también se puede presentar mediante diagramas que contienen flechas, como en las figuras 1 y 2. Las estructuras causales implican que deben aparecer patrones específicos entre los valores de las variables observadas. Esto hace posible utilizar las conexiones entre los valores de las variables observadas para estimar las magnitudes de los efectos postulados y para probar si los datos observados son o no consistentes con los requisitos de las estructuras causales hipotéticas. [4]
El límite entre lo que es y no es un modelo de ecuaciones estructurales no siempre está claro, pero los modelos SE a menudo contienen conexiones causales postuladas entre un conjunto de variables latentes (variables que se cree que existen pero que no se pueden observar directamente, como una actitud, inteligencia o enfermedad mental) y conexiones causales que vinculan las variables latentes postuladas con variables que se pueden observar y cuyos valores están disponibles en algún conjunto de datos. Las variaciones entre los estilos de conexiones causales latentes, las variaciones entre las variables observadas que miden las variables latentes y las variaciones en las estrategias de estimación estadística dan como resultado el conjunto de herramientas SEM que incluye análisis factorial confirmatorio , análisis compuesto confirmatorio , análisis de trayectoria , modelado multigrupo, modelado longitudinal, modelado de trayectoria de mínimos cuadrados parciales , modelado de crecimiento latente y modelado jerárquico o multinivel. [5] [6] [7] [8] [9]
Los investigadores de SEM utilizan programas informáticos para estimar la fuerza y el signo de los coeficientes correspondientes a las conexiones estructurales modeladas, por ejemplo, los números conectados a las flechas de la Figura 1. Debido a que un modelo postulado como el de la Figura 1 puede no corresponder a las fuerzas mundanas que controlan las mediciones de los datos observados, los programas también proporcionan pruebas de modelos y pistas de diagnóstico que sugieren qué indicadores, o qué componentes del modelo, podrían introducir inconsistencias entre el modelo y los datos observados. Las críticas a los métodos SEM apuntan a: desconsideración de las pruebas de modelos disponibles, problemas en la especificación del modelo, una tendencia a aceptar modelos sin considerar la validez externa y posibles sesgos filosóficos. [10]
Una gran ventaja del SEM es que todas estas mediciones y pruebas se realizan simultáneamente en un procedimiento de estimación estadística, donde todos los coeficientes del modelo se calculan utilizando toda la información de las variables observadas. Esto significa que las estimaciones son más precisas que si un investigador calculara cada parte del modelo por separado. [11]
El modelado de ecuaciones estructurales (SEM) comenzó a diferenciarse de la correlación y la regresión cuando Sewall Wright proporcionó interpretaciones causales explícitas para un conjunto de ecuaciones de estilo regresión basadas en una sólida comprensión de los mecanismos físicos y fisiológicos que producen efectos directos e indirectos entre sus variables observadas. [12] [13] [14] Las ecuaciones se estimaron como ecuaciones de regresión ordinarias, pero el contexto sustantivo para las variables medidas permitió una comprensión causal clara, no meramente predictiva. OD Duncan introdujo el SEM en las ciencias sociales en su libro de 1975 [15] y el SEM floreció a fines de la década de 1970 y en la de 1980, cuando el aumento de la potencia informática permitió la estimación práctica de modelos. En 1987, Hayduk [6] proporcionó la primera introducción en forma de libro al modelado de ecuaciones estructurales con variables latentes, y esto fue seguido pronto por el popular texto de Bollen (1989). [16]
En psicología, sociología y economía se desarrollaron enfoques de modelado diferentes pero matemáticamente relacionados. El trabajo inicial de la Comisión Cowles sobre estimación de ecuaciones simultáneas se centró en los algoritmos de Koopman y Hood (1953) de la economía del transporte y el enrutamiento óptimo, con estimación de máxima verosimilitud y cálculos algebraicos de forma cerrada, ya que las técnicas de búsqueda de soluciones iterativas eran limitadas en los días anteriores a las computadoras. La convergencia de dos de estas corrientes de desarrollo (análisis factorial de la psicología y análisis de trayectorias de la sociología a través de Duncan) produjo el núcleo actual de SEM. Uno de los varios programas que Karl Jöreskog desarrolló en Educational Testing Services, LISREL [17] [18] [19] incorporó variables latentes (que los psicólogos conocían como los factores latentes del análisis factorial) dentro de ecuaciones de estilo de análisis de trayectorias (que los sociólogos heredaron de Wright y Duncan). La parte estructurada por factores del modelo incorporó errores de medición que permitieron el ajuste de errores de medición, aunque no necesariamente una estimación libre de errores, de los efectos que conectaban diferentes variables latentes postuladas.
Las huellas de la convergencia histórica de las tradiciones del análisis factorial y del análisis de trayectorias persisten como la distinción entre las partes de medición y estructurales de los modelos; y como continuos desacuerdos sobre la prueba de los modelos, y sobre si la medición debe preceder o acompañar a las estimaciones estructurales. [20] [21] Ver el análisis factorial como una técnica de reducción de datos resta importancia a la prueba, lo que contrasta con la apreciación del análisis de trayectorias para probar conexiones causales postuladas, donde el resultado de la prueba podría indicar una especificación incorrecta del modelo. La fricción entre las tradiciones del análisis factorial y del análisis de trayectorias sigue apareciendo en la literatura.
El análisis de trayectorias de Wright influyó en Hermann Wold, en el alumno de Wold Karl Jöreskog y en el alumno de Jöreskog Claes Fornell, pero el SEM nunca ganó un gran número de seguidores entre los econometristas estadounidenses, posiblemente debido a diferencias fundamentales en los objetivos de modelado y las estructuras de datos típicas. La prolongada separación de la rama económica del SEM condujo a diferencias procedimentales y terminológicas, aunque siguen existiendo profundas conexiones matemáticas y estadísticas. [22] [23] La versión económica del SEM se puede ver en las discusiones de SEMNET sobre endogeneidad, y en el calor producido cuando el enfoque de Judea Pearl sobre la causalidad a través de gráficos acíclicos dirigidos (DAG) roza los enfoques económicos del modelado. [4] Hay disponibles debates que comparan y contrastan varios enfoques SEM [24] [25] pero las diferencias disciplinarias en las estructuras de datos y las preocupaciones que motivan los modelos económicos hacen que la reunión sea poco probable. Pearl [4] extendió el SEM de modelos lineales a no paramétricos, y propuso interpretaciones causales y contrafácticas de las ecuaciones. Los SEM no paramétricos permiten estimar efectos totales, directos e indirectos sin comprometerse con la linealidad de los efectos ni con suposiciones sobre las distribuciones de los términos de error. [25]
Los análisis SEM son populares en las ciencias sociales porque los programas informáticos permiten estimar estructuras causales complejas, pero la complejidad de los modelos introduce una variabilidad sustancial en la calidad de los resultados. Algunos resultados, pero no todos, se obtienen sin el "inconveniente" de comprender el diseño experimental, el control estadístico, las consecuencias del tamaño de la muestra y otras características que contribuyen a un buen diseño de investigación. [ cita requerida ]
Las siguientes consideraciones se aplican a la construcción y evaluación de muchos modelos de ecuaciones estructurales.
Para construir o especificar un modelo es necesario prestar atención a:
Los modelos de ecuaciones estructurales intentan reflejar las fuerzas mundiales que operan en casos causalmente homogéneos, es decir, casos enredados en las mismas estructuras causales mundiales pero cuyos valores en las causas difieren y que, por lo tanto, poseen diferentes valores en las variables de resultado. La homogeneidad causal puede facilitarse mediante la selección de casos o mediante la segregación de casos en un modelo multigrupo. La especificación de un modelo no está completa hasta que el investigador especifica:
El nivel latente de un modelo se compone de variables endógenas y exógenas . Las variables latentes endógenas son las variables de puntuación verdadera que se postulan como receptoras de efectos de al menos otra variable modelada. Cada variable endógena se modela como la variable dependiente en una ecuación de estilo de regresión. Las variables latentes exógenas son variables de fondo que se postulan como causantes de una o más de las variables endógenas y se modelan como las variables predictoras en ecuaciones de estilo de regresión. Las conexiones causales entre las variables exógenas no se modelan explícitamente, pero generalmente se reconocen al modelar las variables exógenas como correlacionadas libremente entre sí. El modelo puede incluir variables intervinientes: variables que reciben efectos de algunas variables pero también envían efectos a otras variables. Al igual que en la regresión, a cada variable endógena se le asigna una variable residual o de error que encapsula los efectos de causas no disponibles y generalmente desconocidas. Se considera que cada variable latente, ya sea exógena o endógena , contiene los puntajes verdaderos de los casos en esa variable, y estos puntajes verdaderos contribuyen causalmente con variaciones válidas/genuinas en una o más de las variables indicadoras observadas/informadas. [26]
El programa LISREL asignó nombres griegos a los elementos de un conjunto de matrices para llevar un registro de los diversos componentes del modelo. Estos nombres se convirtieron en una notación relativamente estándar, aunque la notación se ha extendido y modificado para dar cabida a una variedad de consideraciones estadísticas. [19] [6] [16] [27] Los textos y programas que "simplifican" la especificación del modelo mediante diagramas o mediante el uso de ecuaciones que permiten nombres de variables seleccionados por el usuario, convierten nuevamente el modelo del usuario en una forma estándar de álgebra matricial en segundo plano. Las "simplificaciones" se logran introduciendo implícitamente "suposiciones" predeterminadas del programa sobre las características del modelo con las que los usuarios supuestamente no necesitan preocuparse. Desafortunadamente, estas suposiciones predeterminadas oscurecen fácilmente los componentes del modelo que dejan problemas no reconocidos acechando dentro de la estructura del modelo y las matrices subyacentes.
En el modelo SEM se distinguen dos componentes principales: el modelo estructural que muestra las posibles dependencias causales entre las variables latentes endógenas y exógenas , y el modelo de medición que muestra las conexiones causales entre las variables latentes y los indicadores. Los modelos de análisis factorial exploratorio y confirmatorio , por ejemplo, se centran en las conexiones causales de medición, mientras que los modelos de trayectoria se corresponden más estrechamente con las conexiones estructurales latentes del modelo SEM.
Los modeladores especifican que cada coeficiente de un modelo puede ser estimado libremente o que puede fijarse en algún valor. Los coeficientes libres pueden ser efectos postulados que el investigador desea probar, correlaciones de fondo entre las variables exógenas o las varianzas de las variables residuales o de error que proporcionan variaciones adicionales en las variables latentes endógenas. Los coeficientes fijos pueden ser valores como los valores 1.0 en la Figura 2 que proporcionan una escala para las variables latentes, o valores de 0.0 que afirman desconexiones causales como la afirmación de que no hay efectos directos (sin flechas) que apuntan desde el Logro Académico a cualquiera de las cuatro escalas en la Figura 1. Los programas SEM proporcionan estimaciones y pruebas de los coeficientes libres, mientras que los coeficientes fijos contribuyen de manera importante a probar la estructura general del modelo. También se pueden utilizar varios tipos de restricciones entre los coeficientes. [27] [6] [16] La especificación del modelo depende de lo que se conoce de la literatura, la experiencia del investigador con las variables indicadoras modeladas y las características que se investigan utilizando la estructura específica del modelo.
Existe un límite en cuanto a la cantidad de coeficientes que se pueden estimar en un modelo. Si hay menos puntos de datos que la cantidad de coeficientes estimados, se dice que el modelo resultante es "no identificado" y no se pueden obtener estimaciones de coeficientes. El efecto recíproco y otros bucles causales también pueden interferir con la estimación. [28] [29] [27]
Los coeficientes del modelo fijados en cero, 1,0 u otros valores no requieren estimación porque ya tienen valores especificados. Los valores estimados para los coeficientes del modelo libre se obtienen maximizando el ajuste o minimizando la diferencia con respecto a los datos en relación con las características que tendrían los datos si los coeficientes del modelo libre adoptaran los valores estimados. Las implicaciones del modelo para el aspecto que deberían tener los datos para un conjunto específico de valores de coeficientes dependen de: a) la ubicación de los coeficientes en el modelo (por ejemplo, qué variables están conectadas o desconectadas), b) la naturaleza de las conexiones entre las variables (covarianzas o efectos; a menudo se supone que los efectos son lineales), c) la naturaleza del error o las variables residuales (que a menudo se supone que son independientes o están causalmente desconectadas de muchas variables) y d) las escalas de medición adecuadas para las variables (a menudo se supone que la medición se realiza a nivel de intervalo).
Un efecto más fuerte que conecta dos variables latentes implica que los indicadores de esas variables latentes deberían estar más fuertemente correlacionados. Por lo tanto, una estimación razonable del efecto de una variable latente será cualquier valor que coincida mejor con las correlaciones entre los indicadores de las variables latentes correspondientes, es decir, el valor estimado que maximiza la coincidencia con los datos o minimiza las diferencias con respecto a los datos. Con la estimación de máxima verosimilitud, los valores numéricos de todos los coeficientes del modelo libre se ajustan individualmente (se aumentan o disminuyen progresivamente a partir de los valores iniciales) hasta que maximizan la probabilidad de observar los datos de la muestra, ya sean los datos las covarianzas/correlaciones de las variables o los valores reales de los casos en las variables indicadoras. Las estimaciones de mínimos cuadrados ordinarios son los valores de los coeficientes que minimizan las diferencias al cuadrado entre los datos y cómo se verían los datos si el modelo se especificara correctamente, es decir, si todas las características estimadas del modelo corresponden a características del mundo real.
La característica estadística apropiada para maximizar o minimizar para obtener estimaciones depende de los niveles de medición de las variables (la estimación es generalmente más fácil con mediciones de nivel de intervalo que con medidas nominales u ordinales), y donde una variable específica aparece en el modelo (por ejemplo, las variables dicotómicas endógenas crean más dificultades de estimación que las variables dicotómicas exógenas). La mayoría de los programas SEM proporcionan varias opciones para lo que se debe maximizar o minimizar para obtener estimaciones de los coeficientes del modelo. Las opciones a menudo incluyen estimación de máxima verosimilitud (MLE), máxima verosimilitud con información completa (FIML), mínimos cuadrados ordinarios (OLS), mínimos cuadrados ponderados (WLS), mínimos cuadrados ponderados diagonalmente (DWLS) y mínimos cuadrados en dos etapas. [27]
Un problema común es que el valor estimado de un coeficiente puede ser subidentificado porque no está suficientemente limitado por el modelo y los datos. No existe una mejor estimación única a menos que el modelo y los datos juntos limiten o restrinjan suficientemente el valor de un coeficiente. Por ejemplo, la magnitud de una única correlación de datos entre dos variables es insuficiente para proporcionar estimaciones de un par recíproco de efectos modelados entre esas variables. La correlación puede explicarse por uno de los efectos recíprocos que es más fuerte que el otro efecto, o el otro efecto que es más fuerte que el primero, o por efectos de igual magnitud. Las estimaciones de efectos subidentificados pueden volverse identificadas introduciendo restricciones adicionales del modelo y/o de los datos. Por ejemplo, los efectos recíprocos pueden volverse identificados restringiendo una estimación de efecto para que sea el doble, el triple o equivalente a la otra estimación de efecto, [29] pero las estimaciones resultantes solo serán confiables si la restricción adicional del modelo corresponde a la estructura del mundo. Los datos sobre una tercera variable que causa directamente solo una de un par de variables conectadas causalmente de manera recíproca también pueden ayudar a la identificación. [28] Restringir una tercera variable para que no cause directamente una de las variables recíprocamente causales rompe la simetría que de otro modo afectaría a las estimaciones de efectos recíprocos, porque esa tercera variable debe estar más fuertemente correlacionada con la variable que causa directamente que con la variable en el "otro" extremo del recíproco, sobre la que impacta sólo indirectamente. [28] Nótese que esto nuevamente presupone la idoneidad de la especificación causal del modelo, es decir, que realmente existe un efecto directo que conduce desde la tercera variable a la variable en este extremo de los efectos recíprocos y ningún efecto directo sobre la variable en el "otro extremo" del par de variables recíprocamente conectadas. Las demandas teóricas de efectos nulos/cero proporcionan restricciones útiles que asisten a la estimación, aunque las teorías a menudo no informan claramente qué efectos supuestamente son inexistentes.
La evaluación del modelo depende de la teoría, los datos, el modelo y la estrategia de estimación. Por lo tanto, las evaluaciones del modelo tienen en cuenta lo siguiente:
La investigación que pretende probar o "investigar" una teoría requiere prestar atención a la inconsistencia entre los datos y el modelo, que no es pura casualidad. La estimación ajusta los coeficientes libres del modelo para proporcionar el mejor ajuste posible a los datos. El resultado de los programas SEM incluye una matriz que informa las relaciones entre las variables observadas que se observarían si los efectos estimados del modelo realmente controlaran los valores de las variables observadas. El "ajuste" de un modelo informa la coincidencia o no coincidencia entre las relaciones implícitas del modelo (a menudo covarianzas) y las relaciones observadas correspondientes entre las variables. Las diferencias grandes y significativas entre los datos y las implicaciones del modelo indican problemas. La probabilidad que acompaña a una prueba χ 2 ( chi-cuadrado ) es la probabilidad de que los datos pudieran surgir por variaciones aleatorias del muestreo si el modelo estimado constituyera las fuerzas subyacentes reales de la población. Una probabilidad χ 2 pequeña informa que sería improbable que los datos actuales hubieran surgido si la estructura modelada constituyera las fuerzas causales reales de la población, y las diferencias restantes se atribuyen a variaciones aleatorias del muestreo.
Si un modelo sigue siendo inconsistente con los datos a pesar de seleccionar estimaciones de coeficientes óptimas, una respuesta de investigación honesta informa y atiende a esta evidencia (a menudo una prueba χ2 significativa del modelo). [30] La inconsistencia entre el modelo y los datos más allá de la casualidad desafía tanto las estimaciones de coeficientes como la capacidad del modelo para juzgar la estructura del modelo, independientemente de si la inconsistencia se origina en datos problemáticos, estimación estadística inapropiada o especificación incorrecta del modelo. Las estimaciones de coeficientes en modelos inconsistentes con los datos ("fallidos") son interpretables, como informes de cómo se vería el mundo para alguien que cree en un modelo que entra en conflicto con los datos disponibles. Las estimaciones en modelos inconsistentes con los datos no necesariamente se vuelven "obviamente erróneas" al volverse estadísticamente extrañas o mal firmadas según la teoría. Las estimaciones pueden incluso coincidir estrechamente con los requisitos de una teoría, pero la inconsistencia restante de los datos hace que la coincidencia entre las estimaciones y la teoría no pueda brindar ayuda. Los modelos fallidos siguen siendo interpretables, pero solo como interpretaciones que entran en conflicto con la evidencia disponible.
Es poco probable que la replicación detecte modelos mal especificados que no se ajustan adecuadamente a los datos. Si los datos replicados se encuentran dentro de variaciones aleatorias de los datos originales, es probable que las mismas ubicaciones incorrectas de los coeficientes que proporcionaron un ajuste inadecuado a los datos originales también se ajusten inadecuadamente a los datos replicados. La replicación ayuda a detectar problemas como errores en los datos (cometidos por diferentes grupos de investigación), pero es especialmente débil para detectar especificaciones incorrectas después de la modificación exploratoria del modelo, como cuando se aplica el análisis factorial confirmatorio (AFC) a una segunda mitad aleatoria de datos después del análisis factorial exploratorio (AFE) de los datos de la primera mitad.
Un índice de modificación es una estimación de cuánto "mejoraría" el ajuste de un modelo a los datos (pero no necesariamente cuánto mejoraría la estructura del modelo) si se liberara un coeficiente específico del modelo actualmente fijo para la estimación. Los investigadores que se enfrentan a modelos inconsistentes con los datos pueden liberar fácilmente los coeficientes que los índices de modificación informan como probables de producir mejoras sustanciales en el ajuste. Esto introduce simultáneamente un riesgo sustancial de pasar de un modelo causalmente incorrecto y fallido a un modelo causalmente incorrecto pero que se ajusta porque un ajuste mejorado de los datos no proporciona garantía de que los coeficientes liberados sean sustancialmente razonables o se ajusten al mundo. El modelo original puede contener especificaciones causales erróneas, como efectos dirigidos incorrectamente o suposiciones incorrectas sobre variables no disponibles, y esos problemas no se pueden corregir agregando coeficientes al modelo actual. En consecuencia, esos modelos siguen estando mal especificados a pesar del ajuste más preciso proporcionado por coeficientes adicionales. Es especialmente probable que surjan modelos que se ajusten pero que sean inconsistentes con el mundo si un investigador comprometido con un modelo particular (por ejemplo, un modelo factorial que tenga un número deseado de factores) logra que un modelo que inicialmente falla se ajuste insertando covarianzas de error de medición "sugeridas" por índices de modificación. MacCallum (1986) demostró que "incluso en condiciones favorables, los modelos que surgen de los buscadores de especificaciones deben considerarse con cautela". [31] La especificación incorrecta del modelo a veces puede corregirse mediante la inserción de coeficientes sugeridos por los índices de modificación, pero se plantean muchas más posibilidades correctivas empleando algunos indicadores de variables latentes similares pero significativamente diferentes. [32]
"Aceptar" modelos fallidos como "suficientemente cercanos" tampoco es una alternativa razonable. Browne, MacCallum, Kim, Anderson y Glaser brindaron un ejemplo de advertencia al abordar las matemáticas detrás de por qué la prueba χ 2 puede tener (aunque no siempre tiene) un poder considerable para detectar la especificación incorrecta del modelo. [33] La probabilidad que acompaña a una prueba χ 2 es la probabilidad de que los datos pudieran surgir por variaciones de muestreo aleatorias si el modelo actual, con sus estimaciones óptimas, constituyera las fuerzas subyacentes reales de la población. Una probabilidad χ 2 pequeña informa que sería improbable que los datos actuales hubieran surgido si la estructura del modelo actual constituyera las fuerzas causales reales de la población, y las diferencias restantes se atribuyeran a variaciones de muestreo aleatorias. Browne, McCallum, Kim, Andersen y Glaser presentaron un modelo factorial que consideraron aceptable a pesar de que el modelo era significativamente inconsistente con sus datos según χ 2 . La falacia de su afirmación de que el ajuste cercano debe considerarse suficientemente bueno fue demostrada por Hayduk, Pazkerka-Robinson, Cummings, Levers y Beres [34], quienes demostraron un modelo de ajuste para los propios datos de Browne, et al. incorporando una característica experimental que Browne, et al. pasaron por alto. El error no estaba en las matemáticas de los índices ni en la hipersensibilidad de la prueba χ 2. El error estaba en que Browne, MacCallum y los otros autores olvidaron, descuidaron o pasaron por alto que no se puede confiar en que la cantidad de mal ajuste corresponda a la naturaleza, ubicación o gravedad de los problemas en la especificación de un modelo. [35]
Muchos investigadores intentaron justificar el cambio a índices de ajuste, en lugar de probar sus modelos, afirmando que χ 2 aumenta (y, por lo tanto, la probabilidad de χ 2 disminuye) con el aumento del tamaño de la muestra (N). Hay dos errores en el descuento de χ 2 sobre esta base. Primero, para los modelos adecuados, χ 2 no aumenta con el aumento de N, [30] por lo que si χ 2 aumenta con N, eso en sí mismo es una señal de que algo es detectablemente problemático. Y segundo, para los modelos que están detectablemente mal especificados, χ 2 aumenta con N proporciona la buena noticia de aumentar el poder estadístico para detectar la mala especificación del modelo (es decir, el poder para detectar el error de tipo II). Algunos tipos de malas especificaciones importantes no pueden detectarse por χ 2 , [35] por lo que cualquier cantidad de mal ajuste más allá de lo que podría producirse razonablemente por variaciones aleatorias justifica un informe y una consideración. [36] [30] La prueba del modelo χ 2 , posiblemente ajustada, [37] es la prueba de modelo de ecuación estructural más fuerte disponible.
Numerosos índices de ajuste cuantifican qué tan cerca se ajusta un modelo a los datos, pero todos los índices de ajuste sufren la dificultad lógica de que el tamaño o la cantidad de mal ajuste no está coordinado de manera confiable con la gravedad o naturaleza de los problemas que producen la inconsistencia de los datos. [35] Los modelos con diferentes estructuras causales que se ajustan a los datos de manera idéntica se han llamado modelos equivalentes. [27] Estos modelos son equivalentes a los datos, aunque no causalmente equivalentes, por lo que al menos uno de los llamados modelos equivalentes debe ser inconsistente con la estructura del mundo. Si hay una correlación perfecta de 1.0 entre X e Y y modelamos esto como X causa Y, habrá un ajuste perfecto y un error residual cero. Pero el modelo puede no coincidir con el mundo porque Y puede realmente causar X, o tanto X como Y pueden estar respondiendo a una causa común Z, o el mundo puede contener una mezcla de estos efectos (por ejemplo, como una causa común más un efecto de Y sobre X), u otras estructuras causales. El ajuste perfecto no nos dice que la estructura del modelo se corresponde con la estructura del mundo, y esto a su vez implica que acercarse al ajuste perfecto no necesariamente se corresponde con acercarse a la estructura del mundo –tal vez sí, tal vez no. Esto hace que sea incorrecto que un investigador afirme que incluso un ajuste perfecto del modelo implica que el modelo está correctamente especificado causalmente. Incluso para modelos moderadamente complejos, los modelos con un ajuste equivalente preciso son raros. Los modelos que casi se ajustan a los datos, según cualquier índice, introducen inevitablemente errores de especificación adicionales del modelo potencialmente importantes pero desconocidos. Estos modelos constituyen un impedimento mayor para la investigación.
Esta debilidad lógica hace que todos los índices de ajuste sean "inútiles" siempre que un modelo de ecuación estructural sea significativamente inconsistente con los datos, [36] pero varias fuerzas continúan propagando el uso de índices de ajuste. Por ejemplo, Dag Sorbom informó que cuando alguien le preguntó a Karl Joreskog, el desarrollador del primer programa de modelado de ecuaciones estructurales, "¿Por qué ha agregado GFI?" a su programa LISREL, Joreskog respondió "Bueno, los usuarios nos amenazan diciendo que dejarán de usar LISREL si siempre produce chi-cuadrados tan grandes. Así que tuvimos que inventar algo para hacer felices a las personas. GFI cumple con ese propósito". [38] La evidencia χ 2 de inconsistencia entre el modelo y los datos era demasiado sólida estadísticamente para ser desalojada o descartada, pero al menos se le podía proporcionar a las personas una forma de distraerse de la evidencia "perturbadora". Todavía se pueden obtener beneficios profesionales desarrollando índices adicionales, informando sobre investigaciones del comportamiento de los índices y publicando modelos que oculten intencionalmente la evidencia de la inconsistencia entre los datos y los modelos bajo un MDI (un montón de índices que distraen). No parece haber una justificación general de por qué un investigador debería "aceptar" un modelo causalmente incorrecto, en lugar de intentar corregir las especificaciones erróneas detectadas. Y algunas partes de la literatura parecen no haber notado que "aceptar un modelo" (sobre la base de "satisfacer" un valor de índice) sufre de una versión intensificada de la crítica aplicada a la "aceptación" de una hipótesis nula. Los textos de introducción a las estadísticas generalmente recomiendan reemplazar el término "aceptar" por "no rechazar la hipótesis nula" para reconocer la posibilidad de un error de tipo II. Un error de tipo III surge de "aceptar" una hipótesis de modelo cuando los datos actuales son suficientes para rechazar el modelo.
El compromiso o no de los investigadores con la búsqueda de la estructura del mundo es una preocupación fundamental. Desplazar la evidencia de la inconsistencia de los datos del modelo ocultándola detrás de afirmaciones de índices de ajuste aceptable, introduce el costo para toda la disciplina de desviar la atención de lo que la disciplina podría haber hecho para alcanzar una comprensión estructuralmente mejorada de la sustancia de la disciplina. La disciplina termina pagando un costo real por el desplazamiento basado en índices de la evidencia de la especificación incorrecta del modelo. Las fricciones creadas por los desacuerdos sobre la necesidad de corregir las especificaciones incorrectas del modelo probablemente aumentarán con el uso creciente de modelos no estructurados por factores y con el uso de menos indicadores, pero más precisos, de variables latentes similares pero importantes y diferentes. [32]
Las consideraciones relevantes para el uso de índices de ajuste incluyen la verificación de:
Algunas de las estadísticas de ajuste más comúnmente utilizadas incluyen:
La siguiente tabla proporciona referencias que documentan estas y otras características de algunos índices comunes: el RMSEA (error cuadrático medio de aproximación), el SRMR (residuo cuadrático medio estandarizado), el CFI (índice de ajuste confirmatorio) y el TLI (índice de Tucker-Lewis). En la mayoría de las introducciones a los SEM se pueden encontrar índices adicionales como el AIC (criterio de información de Akaike). [27] Para cada medida de ajuste, una decisión sobre qué representa un ajuste suficientemente bueno entre el modelo y los datos refleja el objetivo del investigador en la elaboración del modelo (quizás desafiar el modelo de otra persona o mejorar la medición); si se debe afirmar o no que el modelo ha sido "probado"; y si el investigador se siente cómodo "ignorando" la evidencia del grado de mal ajuste documentado por el índice. [30]
Los investigadores coinciden en que las muestras deben ser lo suficientemente grandes como para proporcionar estimaciones de coeficientes estables y un poder de prueba razonable, pero no hay un consenso general sobre los tamaños de muestra específicos requeridos, o incluso sobre cómo determinar los tamaños de muestra apropiados. Las recomendaciones se han basado en el número de coeficientes a estimar, el número de variables modeladas y simulaciones de Monte Carlo que abordan coeficientes de modelos específicos. [27] Las recomendaciones de tamaño de muestra basadas en la relación entre el número de indicadores y las variables latentes están orientadas a los factores y no se aplican a los modelos que emplean indicadores únicos que tienen varianzas de error de medición fijas distintas de cero. [32] En general, para modelos de tamaño moderado sin coeficientes estadísticamente difíciles de estimar, los tamaños de muestra requeridos (N) parecen aproximadamente comparables a los N requeridos para una regresión que emplea todos los indicadores.
Cuanto mayor sea el tamaño de la muestra, mayor será la probabilidad de incluir casos que no sean causalmente homogéneos. En consecuencia, aumentar N para mejorar la probabilidad de poder informar un coeficiente deseado como estadísticamente significativo aumenta simultáneamente el riesgo de especificación incorrecta del modelo y la capacidad de detectar la especificación incorrecta. Los investigadores que buscan aprender de sus modelos (incluso aprender potencialmente que su modelo requiere ajuste o reemplazo) se esforzarán por lograr un tamaño de muestra tan grande como lo permitan los fondos y su evaluación de la probable heterogeneidad/homogeneidad causal basada en la población. Si el N disponible es enorme, los subconjuntos de casos de modelado pueden controlar variables que de otro modo podrían alterar la homogeneidad causal. Los investigadores que temen tener que informar las deficiencias de su modelo se debaten entre querer un N mayor para proporcionar suficiente potencia para detectar coeficientes estructurales de interés, mientras evitan la potencia capaz de señalar inconsistencia entre el modelo y los datos. La enorme variación en las estructuras de los modelos y las características de los datos sugiere que se podrían encontrar tamaños de muestra adecuados considerando las experiencias de otros investigadores (tanto buenas como malas) con modelos de tamaño y complejidad comparables que se han estimado con datos similares.
Las interpretaciones causales de los modelos SE son las más claras y comprensibles, pero serán falaces o erróneas si la estructura del modelo no corresponde a la estructura causal del mundo. En consecuencia, la interpretación debe abordar el estado y la estructura generales del modelo, no solo los coeficientes estimados del modelo. El hecho de que un modelo se ajuste a los datos y/o cómo llegó a ajustarse a ellos es fundamental para la interpretación. El ajuste de los datos obtenido mediante la exploración o el seguimiento de índices de modificación sucesivos no garantiza que el modelo sea incorrecto, pero plantea serias dudas porque estos enfoques tienden a modelar incorrectamente las características de los datos. Por ejemplo, explorar para ver cuántos factores se requieren evita encontrar que los datos no están estructurados por factores, especialmente si el modelo factorial ha sido “persuadido” para que se ajuste mediante la inclusión de covarianzas de error de medición. La capacidad de los datos para hablar en contra de un modelo postulado se erosiona progresivamente con cada inclusión injustificada de un efecto “sugerido por un índice de modificación” o una covarianza de error. Resulta extremadamente difícil recuperar un modelo adecuado si el modelo inicial/base contiene varias especificaciones erróneas. [46]
Las estimaciones de efectos directos se interpretan en paralelo a la interpretación de los coeficientes en las ecuaciones de regresión, pero con compromiso causal. Cada aumento unitario en el valor de una variable causal se considera que produce un cambio de la magnitud estimada en el valor de la variable dependiente, dado el control o ajuste de todos los demás mecanismos causales operativos/modelados. Los efectos indirectos se interpretan de manera similar, con la magnitud de un efecto indirecto específico igualando el producto de la serie de efectos directos que comprende ese efecto indirecto. Las unidades involucradas son las escalas reales de los valores de las variables observadas y los valores de escala asignados para las variables latentes. Un efecto especificado/fijo de 1.0 de una variable latente en un indicador específico coordina la escala de ese indicador con la escala de la variable latente. La presunción de que el resto del modelo permanece constante o inmutable puede requerir que se descuenten los efectos indirectos que, en el mundo real, podrían ser provocados simultáneamente por un aumento unitario real. Y el aumento unitario en sí mismo podría ser incoherente con lo que es posible en el mundo real porque puede no haber una manera conocida de cambiar el valor de la variable causal. Si un modelo se ajusta a los errores de medición, el ajuste permite interpretar los efectos de nivel latente como referencias a variaciones en las puntuaciones reales. [26]
Las interpretaciones SEM se apartan más radicalmente de las interpretaciones de regresión cuando una red de coeficientes causales conecta las variables latentes porque las regresiones no contienen estimaciones de efectos indirectos. Las interpretaciones SEM deberían transmitir las consecuencias de los patrones de efectos indirectos que llevan efectos desde las variables de fondo a través de las variables intervinientes hasta las variables dependientes posteriores. Las interpretaciones SEM alientan la comprensión de cómo múltiples vías causales mundiales pueden funcionar en coordinación, o de forma independiente, o incluso contrarrestarse entre sí. Los efectos directos pueden ser contrarrestados (o reforzados) por efectos indirectos, o sus implicaciones correlacionales pueden ser contrarrestadas (o reforzadas) por los efectos de causas comunes. [15] El significado y la interpretación de estimaciones específicas deben contextualizarse en el modelo completo.
La interpretación de los modelos SE debe conectar segmentos causales específicos del modelo con sus implicaciones de varianza y covarianza. Un único efecto directo informa que la varianza en la variable independiente produce una cantidad específica de variación en los valores de la variable dependiente, pero los detalles causales de qué es lo que hace que esto suceda permanecen sin especificar porque un coeficiente de efecto único no contiene subcomponentes disponibles para su integración en una historia estructurada de cómo surge ese efecto. Se requeriría un modelo SE más detallado que incorpore variables que intervengan entre la causa y el efecto para proporcionar características que constituyan una historia sobre cómo funciona un efecto determinado. Hasta que llegue un modelo de este tipo, cada efecto directo estimado conserva un matiz de lo desconocido, invocando así la esencia de una teoría. Una incógnita esencial paralela acompañaría a cada coeficiente estimado incluso en el modelo más detallado, por lo que la sensación de misterio fundamental nunca se erradica por completo de los modelos SE.
Incluso si cada efecto modelado es desconocido más allá de la identidad de las variables involucradas y la magnitud estimada del efecto, las estructuras que vinculan múltiples efectos modelados brindan oportunidades para expresar cómo funcionan las cosas para coordinar las variables observadas, brindando así posibilidades de interpretación útiles. Por ejemplo, una causa común contribuye a la covarianza o correlación entre dos variables afectadas, porque si el valor de la causa aumenta, los valores de ambos efectos también deberían aumentar (suponiendo efectos positivos) incluso si no conocemos la historia completa subyacente a cada causa. [15] (Una correlación es la covarianza entre dos variables que han sido estandarizadas para tener una varianza de 1.0). Otra contribución interpretativa podría hacerse expresando cómo dos variables causales pueden explicar la varianza en una variable dependiente, así como también cómo la covarianza entre dos de esas causas puede aumentar o disminuir la varianza explicada en la variable dependiente. Es decir, la interpretación puede implicar explicar cómo un patrón de efectos y covarianzas puede contribuir a disminuir la varianza de una variable dependiente. [47] La comprensión de las implicaciones causales se conecta implícitamente con la comprensión del “control” y, potencialmente, explica por qué algunas variables, pero no otras, deberían ser controladas. [4] [48] A medida que los modelos se vuelven más complejos, estos componentes fundamentales pueden combinarse de maneras no intuitivas, como explicar cómo no puede haber correlación (covarianza cero) entre dos variables a pesar de que las variables están conectadas por un efecto causal directo distinto de cero. [15] [16] [6] [29]
La insignificancia estadística de una estimación de efecto indica que la estimación podría surgir con bastante facilidad como una variación de muestreo aleatoria en torno a un efecto nulo/cero, por lo que interpretar la estimación como un efecto real se vuelve equívoco. Al igual que en la regresión, la proporción de la varianza de cada variable dependiente explicada por las variaciones en las causas modeladas se proporciona mediante R 2 , aunque se debe utilizar el R 2 de error bloqueado si la variable dependiente está involucrada en efectos recíprocos o en bucle, o si tiene una variable de error correlacionada con la variable de error de cualquier predictor. [49]
Vale la pena repetir la advertencia que aparece en la sección Evaluación del modelo. La interpretación debería ser posible independientemente de que un modelo sea coherente con los datos o no. Las estimaciones indican cómo se vería el mundo para alguien que creyera en el modelo, incluso si esa creencia no tiene fundamento porque el modelo resulta ser erróneo. La interpretación debería reconocer que los coeficientes del modelo pueden corresponder o no a “parámetros”, porque los coeficientes del modelo pueden no tener características estructurales correspondientes en el mundo.
La adición de nuevas variables latentes que entran o salen del modelo original en unas pocas ubicaciones/variables causales claras contribuye a detectar especificaciones erróneas del modelo que, de otro modo, podrían arruinar las interpretaciones de los coeficientes. Las correlaciones entre los nuevos indicadores latentes y todos los indicadores originales contribuyen a probar la estructura del modelo original porque los pocos coeficientes de efecto nuevos y enfocados deben trabajar en coordinación con los efectos directos e indirectos originales del modelo para coordinar los nuevos indicadores con los indicadores originales. Si la estructura del modelo original era problemática, las nuevas conexiones causales dispersas serán insuficientes para coordinar los nuevos indicadores con los indicadores originales, lo que indica la inadecuación de los coeficientes del modelo original a través de la inconsistencia entre el modelo y los datos. [29] Las restricciones correlacionales basadas en coeficientes de efecto nulo/cero y coeficientes a los que se les asignan valores fijos distintos de cero contribuyen tanto a la prueba del modelo como a la estimación de coeficientes y, por lo tanto, merecen reconocimiento como el andamiaje que respalda las estimaciones y su interpretación. [29]
Las interpretaciones se vuelven progresivamente más complejas para los modelos que contienen interacciones, no linealidades, grupos múltiples, niveles múltiples y variables categóricas. [27] Los efectos que afectan a los bucles causales, los efectos recíprocos o los residuos correlacionados también requieren interpretaciones ligeramente revisadas. [6] [29]
Una interpretación cuidadosa de los modelos defectuosos y los que se ajustan puede hacer avanzar la investigación. Para que sea confiable, el modelo debe investigar estructuras causales académicamente informativas, ajustar datos aplicables con estimaciones comprensibles y no incluir coeficientes vacíos. [50] Los modelos que se ajustan de manera confiable son más raros que los modelos defectuosos o los modelos que se ajustan a golpes de manera inapropiada, pero los modelos que se ajustan de manera apropiada son posibles. [34] [51] [52] [53]
Las múltiples formas de conceptualizar los modelos PLS [54] complican la interpretación de los mismos. Muchos de los comentarios anteriores son aplicables si un modelador PLS adopta una perspectiva realista y se esfuerza por garantizar que sus indicadores modelados se combinen de una manera que coincida con alguna variable latente existente pero no disponible. Los modelos PLS no causales, como los que se centran principalmente en R2 o en el poder predictivo fuera de la muestra, cambian los criterios de interpretación al disminuir la preocupación por si los coeficientes del modelo tienen o no contrapartes mundiales. Las características fundamentales que diferencian las cinco perspectivas de modelado PLS analizadas por Rigdon, Sarstedt y Ringle [54] apuntan a diferencias en los objetivos de los modeladores PLS y las diferencias correspondientes en las características del modelo que justifican la interpretación.
Se debe tener cuidado al hacer afirmaciones de causalidad incluso cuando se han realizado experimentos o investigaciones ordenadas en el tiempo. El término modelo causal debe entenderse como "un modelo que transmite supuestos causales", no necesariamente un modelo que produce conclusiones causales validadas (tal vez lo haga, tal vez no). La recopilación de datos en múltiples puntos temporales y el uso de un diseño experimental o cuasiexperimental pueden ayudar a descartar ciertas hipótesis rivales, pero incluso un experimento aleatorio no puede descartar por completo las amenazas a las afirmaciones causales. Ningún diseño de investigación puede garantizar por completo las estructuras causales. [4]
El modelado de ecuaciones estructurales está plagado de controversias. Los investigadores de la tradición analítica factorial comúnmente intentan reducir conjuntos de indicadores múltiples a menos escalas o puntuaciones factoriales más manejables para su uso posterior en modelos estructurados por trayectorias. Esto constituye un proceso gradual en el que el paso de medición inicial proporciona escalas o puntuaciones factoriales que se utilizarán más adelante en un modelo estructurado por trayectorias. Este enfoque gradual parece obvio pero en realidad enfrenta graves deficiencias subyacentes. La segmentación en pasos interfiere con la verificación exhaustiva de si las escalas o puntuaciones factoriales representan válidamente los indicadores y/o informan válidamente sobre los efectos del nivel latente. Un modelo de ecuaciones estructurales que incorpore simultáneamente las estructuras de medición y de nivel latente no solo verifica si los factores latentes coordinan adecuadamente los indicadores, sino que también verifica si esa misma latente coordina simultáneamente de manera apropiada los indicadores de cada latente con los indicadores de las causas teorizadas y/o consecuencias de esa latente. [29] Si una latente no puede realizar ambos estilos de coordinación, se cuestiona la validez de esa latente y se cuestiona una escala o puntajes factoriales que pretendan medir esa latente. Los desacuerdos giraron en torno al respeto o falta de respeto por la evidencia que cuestiona la validez de los factores latentes postulados. Las discusiones a fuego lento, a veces hirvientes, dieron como resultado un número especial de la revista Structural Equation Modeling centrado en un artículo de Hayduk y Glaser [20] seguido de varios comentarios y una réplica, [21] todos disponibles gratuitamente, gracias a los esfuerzos de George Marcoulides.
Estas discusiones alimentaron el desacuerdo sobre si los modelos de ecuaciones estructurales deberían o no ser probados para comprobar su coherencia con los datos, y la prueba de modelos se convirtió en el siguiente foco de las discusiones. Los académicos con antecedentes en modelado de trayectorias tendían a defender la prueba cuidadosa de los modelos, mientras que aquellos con antecedentes en factores tendían a defender la indexación de ajuste en lugar de la prueba de ajuste. Estas discusiones llevaron a un artículo objetivo en Personality and Individual Differences de Paul Barrett [36] que decía: “De hecho, ahora recomendaría prohibir que TODOS esos índices aparezcan en cualquier artículo como indicativos de la “aceptabilidad” o el “grado de desajuste” del modelo”. [36] (página 821). El artículo de Barrett también estaba acompañado de comentarios desde ambas perspectivas. [50] [55]
La controversia sobre la prueba de modelos disminuyó a medida que se volvió obligatoria la notificación clara de inconsistencias significativas entre modelos y datos. Los científicos no pueden ignorar o no informar sobre evidencias solo porque no les guste lo que informan las evidencias. [30] El requisito de prestar atención a las evidencias que apuntan a una especificación incorrecta del modelo sustenta la preocupación más reciente por abordar la “endogeneidad”, un estilo de especificación incorrecta del modelo que interfiere con la estimación debido a la falta de independencia de las variables de error/residuo. En general, la controversia sobre la naturaleza causal de los modelos de ecuaciones estructurales, incluidos los modelos factoriales, también ha estado disminuyendo. Stan Mulaik, un incondicional del análisis factorial, ha reconocido la base causal de los modelos factoriales. [56] Los comentarios de Bollen y Pearl sobre los mitos sobre la causalidad en el contexto del SEM [25] reforzaron la centralidad del pensamiento causal en el contexto del SEM.
Una controversia más breve se centró en los modelos en competencia. Comparar modelos en competencia puede ser muy útil, pero hay cuestiones fundamentales que no se pueden resolver creando dos modelos y conservando el modelo que mejor se ajusta. La sofisticación estadística de presentaciones como la de Levy y Hancock (2007), [57] por ejemplo, hace que sea fácil pasar por alto que un investigador puede comenzar con un modelo terrible y un modelo atroz, y terminar conservando el modelo estructuralmente terrible porque algún índice lo informa como más adecuado que el modelo atroz. Es desafortunado que incluso textos de SEM por lo demás sólidos como Kline (2016) [27] sigan siendo inquietantemente débiles en su presentación de la prueba de modelos. [58] En general, las contribuciones que se pueden hacer mediante el modelado de ecuaciones estructurales dependen de una evaluación cuidadosa y detallada del modelo, incluso si resulta que un modelo fallido es el mejor disponible.
Una controversia adicional que tocó los márgenes de las controversias anteriores espera encenderse. [ cita requerida ] Los modelos factoriales y las estructuras factoriales incorporadas a la teoría que tienen múltiples indicadores tienden a fallar, y la eliminación de indicadores débiles tiende a reducir la inconsistencia entre el modelo y los datos. Reducir el número de indicadores genera preocupación y controversia sobre el número mínimo de indicadores necesarios para respaldar una variable latente en un modelo de ecuación estructural. Se puede persuadir a los investigadores vinculados a la tradición factorial para que reduzcan el número de indicadores a tres por variable latente, pero tres o incluso dos indicadores aún pueden ser inconsistentes con una causa común factorial subyacente propuesta. Hayduk y Littvay (2012) [32] analizaron cómo pensar, defender y ajustar el error de medición cuando se usa solo un indicador único para cada variable latente modelada. Los indicadores únicos se han utilizado de manera efectiva en los modelos SE durante mucho tiempo, [51] pero la controversia sigue estando tan lejos como un revisor que ha considerado la medición solo desde la perspectiva analítica factorial.
Aunque están en declive, los rastros de estas controversias están dispersos por toda la literatura sobre SEM, y es fácil incitar al desacuerdo preguntando: ¿Qué se debe hacer con los modelos que son significativamente inconsistentes con los datos? O preguntando: ¿La simplicidad del modelo prevalece sobre el respeto por la evidencia de inconsistencia de los datos? O, ¿qué peso se debe dar a los índices que muestran un ajuste cercano o no tan cercano de los datos para algunos modelos? O, ¿deberíamos ser especialmente indulgentes con los modelos parsimoniosos que son inconsistentes con los datos y “recompensarlos”? O, dado que el RMSEA tolera que se desestime algún ajuste realmente deficiente para cada grado de libertad del modelo, ¿no significa eso que las personas que prueban modelos con hipótesis nulas de RMSEA no nulo están haciendo pruebas de modelos deficientes? Se requiere una variación considerable en la sofisticación estadística para abordar de manera convincente estas preguntas, aunque las respuestas probablemente se centrarán en la cuestión no técnica de si los investigadores están obligados o no a informar y respetar la evidencia.
Los programas de modelado de ecuaciones estructurales difieren ampliamente en sus capacidades y requisitos de usuario. [66]
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ){{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )