
En matemáticas , el lema de Sperner es un resultado combinatorio sobre coloraciones de triangulaciones , análogo al teorema del punto fijo de Brouwer , que es equivalente a él. [1] Afirma que cada coloración de Sperner (descrita a continuación) de una triangulación de un simplex -dimensional contiene una celda cuyos vértices tienen colores diferentes.
El resultado inicial de este tipo fue demostrado por Emanuel Sperner , en relación con pruebas de invariancia de dominio . Las coloraciones de Sperner se han utilizado para el cálculo eficaz de puntos fijos y en algoritmos de búsqueda de raíces , y se aplican en algoritmos de división justa (corte de torta).
Según la Enciclopedia Matemática Soviética (ed. IM Vinogradov ), un teorema relacionado de 1929 (de Knaster , Borsuk y Mazurkiewicz ) también se conoció como el lema de Sperner ; este punto se analiza en la traducción al inglés (ed. M. Hazewinkel). Ahora se conoce comúnmente como el lema de Knaster-Kuratowski-Mazurkiewicz .

En una dimensión, el lema de Sperner puede considerarse como una versión discreta del teorema del valor intermedio . En este caso, esencialmente dice que si una función discreta toma solo los valores 0 y 1, comienza en el valor 0 y termina en el valor 1, entonces debe cambiar los valores un número impar de veces.
El caso bidimensional es al que se hace referencia con mayor frecuencia. Se afirma lo siguiente:
Subdivida un triángulo ABC arbitrariamente en una triangulación que consta de triángulos más pequeños que se unen de borde a borde. Entonces, una coloración de Sperner de la triangulación se define como una asignación de tres colores a los vértices de la triangulación de modo que
Entonces, cada coloración de Sperner de cada triangulación tiene al menos un "triángulo arcoíris", un triángulo más pequeño en la triangulación que tiene sus vértices coloreados con los tres colores diferentes. Más precisamente, debe haber un número impar de triángulos arcoíris.
En el caso general, el lema se refiere a un simplex de n dimensiones :
Considere cualquier triangulación T , una división disjunta de en simples n -dimensionales más pequeños, que nuevamente se encuentran cara a cara. Denota la función colorante como:
donde S es el conjunto de vértices de T . Una función de coloración define una coloración de Sperner cuando:
están coloreados sólo con los colores
Entonces, cada coloración de Sperner de cada triangulación del simplex de n dimensiones tiene un número impar de instancias de un simplex arcoíris , es decir, un simplex cuyos vértices están coloreados con todos los n + 1 colores. En particular, debe haber al menos un arcoíris simplex.

Primero abordaremos el caso bidimensional. Considere un gráfico G construido a partir de la triangulación T de la siguiente manera:
Tenga en cuenta que en el intervalo AB hay un número impar de bordes coloreados 1-2 (simplemente porque A es de color 1, B es de color 2; y a medida que avanzamos a lo largo de AB , debe haber un número impar de cambios de color para obtener diferentes colores al principio y al final). En los intervalos BC y CA, no hay ningún borde coloreado 1-2. Por tanto, el vértice de G correspondiente al área exterior tiene un grado impar. Pero se sabe (el lema del apretón de manos ) que en un gráfico finito hay un número par de vértices con grado impar. Por lo tanto, el gráfico restante, excluyendo el área exterior, tiene un número impar de vértices con grado impar correspondiente a miembros de T.
Se puede ver fácilmente que el único grado posible de un triángulo a partir de T es 0, 1 o 2, y que el grado 1 corresponde a un triángulo coloreado con los tres colores 1, 2 y 3.
Así hemos obtenido una conclusión ligeramente más sólida, que dice que en una triangulación T hay un número impar (y al menos uno) de triángulos de colores.
Un caso multidimensional se puede demostrar mediante inducción sobre la dimensión de un simplex. Aplicamos el mismo razonamiento, que en el caso bidimensional, para concluir que en una triangulación de n dimensiones hay un número impar de simples de colores.
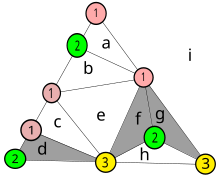

Aquí hay una elaboración de la prueba dada anteriormente, para un lector nuevo en la teoría de grafos .
Este diagrama numera los colores de los vértices del ejemplo dado anteriormente. Los pequeños triángulos cuyos vértices tienen números diferentes están sombreados en el gráfico. Cada pequeño triángulo se convierte en un nodo en el nuevo gráfico derivado de la triangulación. Las letras minúsculas identifican las áreas, ocho dentro de la figura, y el área i designa el espacio fuera de ella.
Como se describió anteriormente, aquellos nodos que comparten un borde cuyos puntos finales están numerados 1 y 2 se unen en el gráfico derivado. Por ejemplo, el nodo d comparte un borde con el área exterior i y todos sus vértices tienen números diferentes, por lo que también está sombreado. El nodo b no está sombreado porque dos vértices tienen el mismo número, pero está unido al área exterior.
Se podría agregar un nuevo triángulo con número completo, por ejemplo, insertando un nodo numerado 3 en el borde entre 1 y 1 del nodo a y uniendo ese nodo al otro vértice de a . Hacerlo tendría que crear un par de nodos nuevos, como en la situación con los nodos f y g .
Andrew McLennan y Rabee Tourky presentaron una prueba diferente, utilizando el volumen de un simplex . Procede en un solo paso, sin inducción. [2] [3]
Supongamos que hay un símplex d -dimensional de longitud de lado N y que está triangulado en subsímplices de longitud de lado 1. Hay una función que, dado cualquier vértice de la triangulación, devuelve su color. Se garantiza que la coloración satisface la condición límite de Sperner. ¿Cuántas veces tenemos que llamar a la función para encontrar un arco iris simplex? Obviamente, podemos repasar todos los vértices de triangulación, cuyo número es O( N d ), que es polinomio en N cuando la dimensión es fija. Pero, ¿se puede hacer en el tiempo O(poly(log N )), que es polinomio en la representación binaria de N?
Este problema fue estudiado por primera vez por Christos Papadimitriou . Introdujo una clase de complejidad llamada PPAD , que contiene esto y problemas relacionados (como encontrar un punto fijo de Brouwer ). Demostró que encontrar un Sperner simplex es PPAD completo incluso para d =3. Unos 15 años después, Chen y Deng demostraron que el PPAD era completo incluso para d =2. [4] Se cree que los problemas difíciles de PPAD no se pueden resolver en el tiempo O (poli (log N )).
Supongamos que cada vértice de la triangulación puede estar etiquetado con varios colores, de modo que la función de coloración sea F : S → 2 [ n +1] .
Para cada subsímplex, el conjunto de etiquetas en sus vértices es una familia de conjuntos sobre el conjunto de colores [ n + 1] . Esta familia de conjuntos puede verse como un hipergrafo .
Si, para cada vértice v en una cara del símplex, los colores en f ( v ) son un subconjunto del conjunto de colores en los puntos finales de la cara, entonces existe un subsímplex con un etiquetado equilibrado : un etiquetado en el que el El hipergrafo correspondiente admite un emparejamiento fraccionario perfecto . Para ilustrar, aquí hay algunos ejemplos de etiquetado equilibrado para n = 2 :
Esto fue demostrado por Shapley en 1973. [5] Es un análogo combinatorio del lema KKMS .
Supongamos que tenemos un politopo P d -dimensional con n vértices. P está triangulado y cada vértice de la triangulación está etiquetado con una etiqueta de {1,…, n }. Cada vértice principal i está etiquetado como i . Un subsímplejo se llama completamente etiquetado si es d -dimensional y cada uno de sus d + 1 vértices tiene una etiqueta diferente. Si cada vértice en una cara F de P está etiquetado con una de las etiquetas en los puntos finales de F , entonces hay al menos n – d símplices completamente etiquetados. Algunos casos especiales son:
La afirmación general fue conjeturada por Atanassov en 1996, quien la demostró para el caso d = 2 . [6] La prueba del caso general fue dada por primera vez por De Loera, Peterson y Su en 2002. [7] Proporcionan dos pruebas: la primera no es constructiva y utiliza la noción de conjuntos de guijarros ; el segundo es constructivo y se basa en argumentos de seguir caminos en gráficos .
Meunier [8] extendió el teorema de los politopos a los cuerpos politópicos, que no necesitan ser convexos o simplemente conexos. En particular, si P es un politopo, entonces el conjunto de sus caras es un cuerpo politopo. En cada etiquetado de Sperner de un cuerpo politópico con vértices v 1 , …, vn , hay al menos:
simples completamente etiquetados de modo que cualquier par de estos simples reciba dos etiquetas diferentes. El grado grado B ( P ) ( vi ) es el número de aristas de B ( P ) a las que pertenece vi . Dado que el grado es al menos d , el límite inferior es al menos n – d . Pero puede ser más grande. Por ejemplo, para el politopo cíclico en 4 dimensiones con n vértices, el límite inferior es:
Musin [9] amplió aún más el teorema a variedades lineales por partes d -dimensionales , con o sin límite.
Asada, Frick, Pisharody, Polevy, Stoner, Tsang y Wellner [10] ampliaron aún más el teorema a pseudovariedades con límite y mejoraron el límite inferior del número de facetas con etiquetas de pares distintos.
Supongamos que, en lugar de un simplex triangulado en subsímplices, tenemos un cubo de n dimensiones dividido en cubos de n dimensiones más pequeños.
Harold W. Kuhn [11] demostró el siguiente lema. Supongamos que el cubo [0, M ] n , para algún número entero M , se divide en M n cubos unitarios. Supongamos que cada vértice de la partición está etiquetado con una etiqueta de {1,…, n + 1}, de modo que para cada vértice v : (1) si v i = 0 entonces la etiqueta en v es como máximo i ; (2) si v i = M entonces la etiqueta de v no es i . Entonces existe un cubo unitario con todas las etiquetas {1,…, n + 1} (algunas de ellas más de una vez). El caso especial n = 2 es: supongamos que un cuadrado se divide en subcuadrados y cada vértice está etiquetado con una etiqueta de {1,2,3}. El borde izquierdo está etiquetado con 1 (= como máximo 1); el borde inferior está etiquetado con 1 o 2 (= como máximo 2); el borde superior está etiquetado con 1 o 3 (= no 2); y el borde derecho está etiquetado con 2 o 3 (= no 1). Luego hay un cuadrado etiquetado con 1,2,3.
Otra variante, relacionada con el teorema de Poincaré-Miranda , [12] es la siguiente. Supongamos que el cubo [0, M ] n se divide en M n cubos unitarios. Supongamos que cada vértice está etiquetado con un vector binario de longitud n , tal que para cada vértice v : (1) si v i = 0 entonces la coordenada i de la etiqueta en v es 0; (2) si v i = M entonces la coordenada i de la etiqueta en v es 1; (3) si dos vértices son vecinos, entonces sus etiquetas difieren como máximo en una coordenada. Entonces existe un cubo unitario en el que las 2 n etiquetas son diferentes. En dos dimensiones, otra forma de formular este teorema es: [13] en cualquier etiquetado que satisfaga las condiciones (1) y (2), hay al menos una celda en la que la suma de etiquetas es 0 [una celda unidimensional con (1,1) y (-1,-1) etiquetas, o celdas bidimensionales con las cuatro etiquetas diferentes].
Wolsey [14] reforzó estos dos resultados demostrando que el número de cubos completamente etiquetados es impar.
Musin [13] amplió estos resultados a cuadrangulaciones generales .
Supongamos que, en lugar de un único etiquetado, tenemos n etiquetados de Sperner diferentes. Consideramos pares (símplex, permutación) tales que la etiqueta de cada vértice del simplex se elige de un etiquetado diferente (por lo que para cada simplex, hay n ! pares diferentes). Entonces hay al menos n ! pares completamente etiquetados. Esto fue demostrado por Ravindra Bapat [15] para cualquier triangulación. Más tarde, Su presentó una prueba más sencilla, que sólo funciona para triangulaciones específicas. [dieciséis]
Otra forma de enunciar este lema es la siguiente. Supongamos que hay n personas, cada una de las cuales produce un etiquetado de Sperner diferente de la misma triangulación. Entonces, existe un simplex y una coincidencia de las personas con sus vértices, de modo que cada vértice es etiquetado por su propietario de manera diferente (una persona etiqueta su vértice con 1, otra persona etiqueta su vértice con 2, etc.). Además, hay al menos n ! tales coincidencias. Esto se puede utilizar para encontrar un corte de pastel sin envidia con piezas conectadas.
Asada, Frick, Pisharody, Polevy, Stoner, Tsang y Wellner [10] extendieron este teorema a pseudovariedades con límite.
De manera más general, supongamos que tenemos m etiquetados de Sperner diferentes, donde m puede ser diferente de n . Entonces: [17] : Thm 2.1
Ambas versiones se reducen al lema de Sperner cuando m = 1 , o cuando todos los m etiquetados son idénticos.
Véase [18] para generalizaciones similares.
Brown y Cairns [19] reforzaron el lema de Sperner al considerar la orientación de los simples. Cada subsímplex tiene una orientación que puede ser +1 o -1 (si está completamente etiquetado) o 0 (si no está completamente etiquetado). Demostraron que la suma de todas las orientaciones de los simples es +1. En particular, esto implica que hay un número impar de simples completamente etiquetados.
Como ejemplo para n = 3 , supongamos que un triángulo está triangulado y etiquetado con {1,2,3}. Considere la secuencia cíclica de etiquetas en el límite del triángulo. Defina el grado del etiquetado como el número de cambios de 1 a 2, menos el número de cambios de 2 a 1. Consulte los ejemplos en la tabla de la derecha. Tenga en cuenta que el grado es el mismo si contamos los cambios de 2 a 3 menos 3 a 2, o de 3 a 1 menos 1 a 3.
Musin demostró que el número de triángulos completamente etiquetados es al menos el grado del etiquetado . [20] En particular, si el grado es distinto de cero, entonces existe al menos un triángulo completamente etiquetado.
Si un etiquetado satisface la condición de Sperner, entonces su grado es exactamente 1: hay 1-2 y 2-1 interruptores sólo en el lado entre los vértices 1 y 2, y el número de 1-2 interruptores debe ser uno más que el número de 2-1 interruptores (al caminar del vértice 1 al vértice 2). Por tanto, el lema de Sperner original se deriva del teorema de Musin.
Existe un lema similar sobre árboles y ciclos finitos e infinitos . [21]
Mirzakhani y Vondrak [22] estudian una variante más débil del etiquetado de Sperner, en el que el único requisito es que la etiqueta i no se utilice en la cara opuesta al vértice i . Lo llaman etiquetado admisible según Sperner . Muestran que existen etiquetados admisibles por Sperner en los que cada celda contiene como máximo 4 etiquetas. También demuestran un límite inferior óptimo para el número de celdas que deben tener al menos dos etiquetas diferentes en cada etiquetado admisible por Sperner. También prueban que, para cualquier partición del simplex regular admisible por Sperner, la partición de Voronoi minimiza el área total del límite entre las partes .
Las coloraciones de Sperner se han utilizado para el cálculo eficaz de puntos fijos . Se puede construir una coloración de Sperner de modo que los simples completamente etiquetados correspondan a puntos fijos de una función determinada. Al hacer una triangulación cada vez más pequeña, se puede demostrar que el límite de los simples completamente etiquetados es exactamente el punto fijo. Por tanto, la técnica proporciona una forma de aproximar puntos fijos. Una aplicación relacionada es la detección numérica de órbitas periódicas y dinámica simbólica . [23] El lema de Sperner también se puede utilizar en algoritmos de búsqueda de raíces y algoritmos de división justa ; consulte los protocolos Simmons-Su .
El lema de Sperner es uno de los ingredientes clave de la demostración del teorema de Monsky , de que un cuadrado no puede dividirse en un número impar de triángulos de áreas iguales . [24]
El lema de Sperner puede utilizarse para encontrar un equilibrio competitivo en una economía de intercambio , aunque existen formas más eficientes de encontrarlo. [25] : 67
Cincuenta años después de publicarlo por primera vez, Sperner presentó un estudio sobre el desarrollo, influencia y aplicaciones de su lema combinatorio. [26]
Hay varios teoremas de punto fijo que vienen en tres variantes equivalentes: una variante de topología algebraica , una variante combinatoria y una variante de cobertura de conjuntos. Cada variante se puede demostrar por separado utilizando argumentos totalmente diferentes, pero cada variante también se puede reducir a las demás variantes de su fila. Además, cada resultado de la fila superior se puede deducir del que se encuentra debajo en la misma columna. [27]