Circuito distorsionado

Protocolo criptográfico para computación entre dos partes

El circuito ilegible es un protocolo criptográfico que permite el cálculo seguro entre dos partes , en el que dos partes que desconfían pueden evaluar conjuntamente una función sobre sus entradas privadas sin la presencia de un tercero de confianza. En el protocolo de circuito ilegible, la función debe describirse como un circuito booleano .

La historia de los circuitos ilegibles es complicada. La invención del circuito ilegible se le atribuye a Andrew Yao , ya que Yao presentó la idea en la presentación oral de un artículo ^[1] en FOCS '86. Esto fue documentado por Oded Goldreich en 2003. ^[2] El primer documento escrito sobre esta técnica fue de Goldreich, Micali y Wigderson en STOC '87. ^[3] El término "circuito ilegible" fue utilizado por primera vez por Beaver, Micali y Rogaway en STOC'90. ^[4] El protocolo de Yao para resolver el problema de los millonarios fue el ejemplo inicial de computación segura, pero no está directamente relacionado con los circuitos ilegibles.

Fondo

Transferencia inconsciente

En el protocolo de circuito ilegible, utilizamos la transferencia inconsciente . En la transferencia inconsciente, se transfiere una cadena entre un emisor y un receptor de la siguiente manera: un emisor tiene dos cadenas y . El receptor elige y el emisor envía con el protocolo de transferencia inconsciente de tal manera que ${\displaystyle S_{0}}$ ${\displaystyle S_{1}}$ ${\displaystyle b\in \{0,1\}}$ ${\displaystyle S_{b}}$

1. El receptor no obtiene ninguna información sobre la cadena no enviada . ${\displaystyle S_{(1-b)}}$
2. El valor de no está expuesto al remitente. ${\displaystyle b}$

Tenga en cuenta que, si bien el receptor no conoce los valores, en la práctica conoce cierta información sobre lo que codifica, de modo que no elige a ciegas . Es decir, si codifica un valor falso, codifica un valor verdadero y el receptor desea obtener el valor verdadero codificado, elige . ${\displaystyle S_{0},S_{1}}$ ${\displaystyle S_{b}}$ ${\displaystyle b}$ ${\displaystyle S_{0}}$ ${\displaystyle S_{1}}$ ${\displaystyle b=1}$

La transferencia inconsciente se puede construir utilizando criptografía asimétrica como el criptosistema RSA .

Definiciones y notaciones

El operador es una concatenación de cadenas . El operador es un XOR bit a bit . k es un parámetro de seguridad y la longitud de las claves. Debe ser mayor que 80 y normalmente se establece en 128. ${\displaystyle \parallel }$ ${\displaystyle \oplus }$

Protocolo de circuito ilegible

El protocolo consta de 6 pasos como se detalla a continuación:

1. La función subyacente (por ejemplo, en el problema de los millonarios, la función de comparación) se describe como un circuito booleano con compuertas de 2 entradas. El circuito es conocido por ambas partes. Este paso puede ser realizado de antemano por un tercero.
2. Alice distorsiona (encripta) el circuito. Llamamos a Alice la distorsionadora .
3. Alice envía el circuito distorsionado a Bob junto con su entrada cifrada.
4. Para calcular el circuito, Bob también necesita codificar su propia entrada. Para ello, necesita la ayuda de Alice, ya que sólo el codificador sabe cómo cifrar. Finalmente, Bob puede cifrar su entrada mediante una transferencia inconsciente. En términos de la definición anterior, Bob es el receptor y Alice el emisor en esta transferencia inconsciente.
5. Bob evalúa (descifra) el circuito y obtiene las salidas cifradas. A Bob lo llamamos evaluador .
6. Alice y Bob se comunican para conocer el resultado.

Generación de circuitos

El circuito booleano para funciones pequeñas se puede generar a mano. Es convencional hacer el circuito con puertas XOR y AND de 2 entradas . Es importante que el circuito generado tenga el número mínimo de puertas AND (ver Optimización XOR libre). Hay métodos que generan el circuito optimizado en términos de número de puertas AND utilizando la técnica de síntesis lógica . ^[5] El circuito para el Problema de los Millonarios es un circuito comparador digital (que es una cadena de sumadores completos que funcionan como un restador y emiten el indicador de acarreo ). Se puede implementar un circuito sumador completo utilizando solo una puerta AND y algunas puertas XOR . Esto significa que el número total de puertas AND para el circuito del Problema de los Millonarios es igual al ancho de bits de las entradas.

Confuso

Cables y sus etiquetas en una puerta AND

Construcción de la tabla de verdad de una compuerta AND

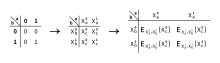
Alice (garbler) encripta el circuito booleano en este paso para obtener un circuito ilegible . Alice asigna dos cadenas generadas aleatoriamente llamadas etiquetas a cada cable del circuito: una para el 0 semántico booleano y otra para el 1. (La etiqueta tiene una longitud de k bits, donde k es el parámetro de seguridad , y normalmente se establece en 128). A continuación, va a todas las puertas del circuito y reemplaza 0 y 1 en las tablas de verdad con las etiquetas correspondientes. La siguiente tabla muestra la tabla de verdad para una puerta AND con dos entradas y una salida : ${\displaystyle w^{a},w^{b}}$ ${\displaystyle w^{c}}$

Alice reemplazó 0 y 1 con las etiquetas correspondientes:

Luego, encripta la entrada de salida de la tabla de verdad con las dos etiquetas de entrada correspondientes. La tabla encriptada se llama tabla ilegible. Esto se hace de tal manera que uno puede desencriptar la tabla ilegible solo si tiene las dos etiquetas de entrada correctas. En la tabla a continuación, hay un cifrado simétrico de doble clave en el que k es la clave secreta y X es el valor que se va a encriptar (ver Cifrado en bloque de clave fija). ${\displaystyle Enc_{k}(X)}$

Después de esto, Alice permuta aleatoriamente la tabla de modo que el valor de salida no se pueda determinar a partir de la fila. El nombre del protocolo, garbled , se deriva de esta permutación aleatoria.

Transferencia de datos

Alice envía las tablas ilegibles calculadas para todas las puertas del circuito a Bob. Bob necesita etiquetas de entrada para abrir las tablas ilegibles. Por lo tanto, Alice elige las etiquetas correspondientes a su entrada y se las envía a Bob. Por ejemplo, si la entrada de Alice es , entonces envía , , , y a Bob. Bob no aprenderá nada sobre la entrada de Alice, , ya que Alice genera aleatoriamente las etiquetas y Bob las ve como cadenas aleatorias. ${\displaystyle a}$ ${\displaystyle \mathbf {a} =a_{4}a_{3}a_{2}a_{1}a_{0}=01101}$ ${\displaystyle X_{0}^{a_{4}}}$ ${\displaystyle X_{1}^{a_{3}}}$ ${\displaystyle X_{1}^{a_{2}}}$ ${\displaystyle X_{0}^{a_{1}}}$ ${\displaystyle X_{1}^{a_{0}}}$ ${\displaystyle \mathbf {a} }$

Bob también necesita las etiquetas correspondientes a su entrada. Recibe sus etiquetas a través de transferencias inconscientes para cada bit de su entrada. Por ejemplo, si la entrada de Bob es , Bob primero solicita entre las etiquetas de Alice y . A través de una transferencia inconsciente de 1 de cada 2 , recibe y así sucesivamente. Después de las transferencias inconscientes , Alice no aprenderá nada sobre la entrada de Bob y Bob no aprenderá nada sobre las otras etiquetas. ${\displaystyle \mathbf {b} =b_{4}b_{3}b_{2}b_{1}b_{0}=10100}$ ${\displaystyle b_{0}=0}$ ${\displaystyle X_{0}^{b_{0}}}$ ${\displaystyle X_{1}^{b_{0}}}$ ${\displaystyle X_{0}^{b_{0}}}$

Evaluación

Después de la transferencia de datos, Bob tiene las tablas ilegibles y las etiquetas de entrada. Pasa por todas las puertas una por una e intenta descifrar las filas en las tablas ilegibles. Puede abrir una fila para cada tabla y recuperar la etiqueta de salida correspondiente: , donde . Continúa la evaluación hasta que llega a las etiquetas de salida. ${\displaystyle X^{c}=Dec_{X^{a},X^{b}}(garbled\_table[i])}$ ${\displaystyle 0\leq i\leq 3}$

Salida reveladora

Después de la evaluación, Bob obtiene la etiqueta de salida, y Alice conoce su correspondencia con el valor booleano, ya que tiene ambas etiquetas: y . Alice puede compartir su información con Bob o Bob puede revelar la salida a Alice de modo que uno o ambos conozcan la salida. ${\displaystyle X^{c}}$ ${\displaystyle X_{0}^{c}}$ ${\displaystyle X_{1}^{c}}$

Mejoramiento

Punto y permutación

En esta optimización, Alice genera un bit aleatorio, , llamado bit de selección para cada cable . Establece el primer bit de la etiqueta 0, en y el primer bit de la etiqueta 1, , en ( NO de ). Hace lo mismo para el cable . Luego, en lugar de permutar aleatoriamente, ordena la tabla ilegible según los bits de selección de entrada. De esta manera, Bob no necesita probar las cuatro filas de la tabla para encontrar la correcta, ya que recibe los bits de puntero con cada etiqueta de cable y puede encontrar la fila correcta y descifrarla con un intento. Esto reduce la carga de evaluación en 4 veces. Tampoco revela nada sobre el valor de salida porque los bits de selección se generan aleatoriamente. ^[6] ${\displaystyle s}$ ${\displaystyle w}$ ${\displaystyle X_{0}^{a}}$ ${\displaystyle s}$ ${\displaystyle X_{1}^{a}}$ ${\displaystyle {\bar {s}}}$ ${\displaystyle s}$ ${\displaystyle w^{b}}$

Reducción de filas

Esta optimización reduce el tamaño de las tablas ilegibles de 4 filas a 3 filas. Aquí, en lugar de generar una etiqueta para el cable de salida de una compuerta de forma aleatoria, Alice la genera utilizando una función de las etiquetas de entrada. Genera las etiquetas de salida de modo que la primera entrada de la tabla ilegible se convierta en 0 y ya no sea necesario enviarla: ^[7]

${\displaystyle {\begin{aligned}&Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})=0\\&X_{0}^{c}=Dec_{X_{0}^{a},X_{0}^{b}}(0).\end{aligned}}}$

XOR libre

En esta optimización, Alice genera un valor aleatorio global de (k-1) bits que se mantiene en secreto. Durante la codificación de las puertas de entrada y , solo genera las etiquetas y calcula las otras etiquetas como y . Con estos valores, la etiqueta del cable de salida de una puerta XOR con cables de entrada , se establece en . La prueba de seguridad en el modelo de oráculo aleatorio para esta optimización se proporciona en el artículo Free-XOR. ^[8] ${\displaystyle R}$ ${\displaystyle w^{a}}$ ${\displaystyle w^{b}}$ ${\displaystyle (X_{0}^{a},X_{0}^{b})}$ ${\displaystyle X_{1}^{a}=X_{0}^{a}\oplus (R\parallel 1)}$ ${\displaystyle X_{1}^{b}=X_{0}^{b}\oplus (R\parallel 1)}$ ${\displaystyle w^{c}}$ ${\displaystyle w^{a}}$ ${\displaystyle w^{b}}$ ${\displaystyle X^{c}=X^{a}\oplus X^{b}}$

Implicación

La optimización XOR libre implica un punto importante: la cantidad de transferencia de datos (comunicación) y la cantidad de cifrados y descifrados (cálculos) del protocolo de circuito ilegible dependen únicamente del número de puertas AND en el circuito booleano , no de las puertas XOR . Por lo tanto, entre dos circuitos booleanos que representan la misma función, se prefiere el que tenga el menor número de puertas AND.

Cifrado de bloques de clave fija

Este método permite codificar y evaluar de manera eficiente las puertas AND utilizando AES de clave fija , en lugar de una costosa función hash criptográfica como SHA-2 . En este esquema de codificación, que es compatible con las técnicas Free XOR y Row Reduction, la clave de salida se cifra con el token de entrada y utilizando la función de cifrado , donde , es un cifrado de bloque de clave fija (por ejemplo, instanciado con AES ), y es un número único por puerta (por ejemplo, identificador de puerta) llamado tweak . ^[9] ${\displaystyle X^{c}}$ ${\displaystyle X^{a}}$ ${\displaystyle X^{b}}$ ${\displaystyle Enc(X^{a},X^{b},T,X^{c})=\pi (K)\oplus K\oplus X^{c}}$ ${\displaystyle K=2X^{a}\oplus 4X^{b}\oplus T}$ ${\displaystyle \pi }$ ${\displaystyle T}$

Mitad y

Esta optimización reduce el tamaño de la tabla ilegible para las puertas AND de 3 filas en la reducción de filas a 2 filas. Se demuestra que este es el mínimo teórico para la cantidad de filas en la tabla ilegible, para una cierta clase de técnicas de ilegibilidad. ^[10]

Seguridad

El circuito de Yao Garbled es seguro contra un adversario semihonesto. Este tipo de adversario sigue el protocolo y no realiza ningún comportamiento malicioso, pero intenta violar la privacidad de la entrada de la otra parte al examinar los mensajes transmitidos en el protocolo.

Es más difícil hacer que este protocolo sea seguro contra un adversario malicioso que se desvíe del protocolo. Una de las primeras soluciones para hacer que el protocolo sea seguro contra adversarios maliciosos es usar una prueba de conocimiento cero para evitar actividades maliciosas durante el protocolo. ^[11] Durante años, este enfoque se consideró más una solución teórica que una solución práctica debido a los costos de complejidad que implica. Pero se ha demostrado que es posible usarlo con solo un pequeño costo. ^[12] Otro enfoque es usar varios GC para un circuito y verificar la corrección de un subconjunto de ellos y luego usar el resto para el cálculo con la esperanza de que si el ilegible fuera malicioso, se detectaría durante la fase de verificación. ^[13] Otra solución es hacer que el esquema de ilegible sea autenticado de modo que el evaluador pueda verificar el circuito ilegible. ^{[14] [15]}

Véase también

• Criptografía
• Sociedad Anónima
• Computación segura entre múltiples partes
• El problema de los millonarios de Yao

Referencias

1. Yao, Andrew Chi-Chih (1986). "Cómo generar e intercambiar secretos". 27.º Simposio anual sobre fundamentos de la informática (SFCS 1986) . pp. 162-167. doi :10.1109/SFCS.1986.25. ISBN 978-0-8186-0740-0.
2. Goldreich, Oded (2003). "Criptografía y protocolos criptográficos". Computación distribuida: artículos para celebrar el 20.º aniversario de PODC . 16 (2–3): 177–199. CiteSeerX 10.1.1.117.3618 . doi :10.1007/s00446-002-0077-1. S2CID  9966766. 
3. Goldreich, Oded; Micali, Silvio; Wigderson, Avi (1987). "Cómo jugar a CUALQUIER juego mental". Actas de la decimonovena conferencia anual de la ACM sobre teoría de la computación - STOC '87 . págs. 218-229. doi :10.1145/28395.28420. ISBN 978-0897912211.S2CID6669082  .​
4. Beaver, Donald; Micali, Silvio; Rogaway, Phillip (1990). "La complejidad circular de los protocolos seguros". Actas del vigésimo segundo simposio anual de la ACM sobre teoría de la computación - STOC '90 . págs. 503–513. CiteSeerX 10.1.1.697.1624 . doi :10.1145/100216.100287. ISBN .  978-0897913614.S2CID1578121  .​
5. Songhori, Ebrahim M; Hussain, Siam U; Sadeghi, Ahmad-Reza; Schneider, Thomas; Koushanfar, Farinaz (2015). "TinyGarble: circuitos confusos secuenciales escalables y altamente comprimidos". Simposio IEEE 2015 sobre seguridad y privacidad. págs. 411–428. doi :10.1109/SP.2015.32. ISBN 978-1-4673-6949-7.S2CID 5346323  .
6. Beaver, Donald; Micali, Silvio; Rogaway, Phillip (1990). "La complejidad circular de los protocolos seguros". Actas del vigésimo segundo simposio anual de la ACM sobre teoría de la computación - STOC '90 . págs. 503–513. CiteSeerX 10.1.1.697.1624 . doi :10.1145/100216.100287. ISBN .  978-0897913614.S2CID1578121  .​
7. Naor, Moni; Pinkas, Benny; Sumner, Reuban (1999). "Subastas que preservan la privacidad y diseño de mecanismos". Actas de la 1.ª conferencia de la ACM sobre comercio electrónico . pp. 129–139. CiteSeerX 10.1.1.17.7459 . doi :10.1145/336992.337028. ISBN .  978-1581131765. Número de identificación del sujeto  207593367.
8. Kolesnikov, Vladimir; Schneider, Thomas (2008). "Circuito ilegible mejorado: puertas XOR gratuitas y aplicaciones". Autómatas, lenguajes y programación . Apuntes de clase en informática. Vol. 5126. págs. 486–498. CiteSeerX 10.1.1.160.5268 . doi :10.1007/978-3-540-70583-3_40. ISBN.  978-3-540-70582-6.
9. Bellare, Mihir; Hoang, Viet Tung; Keelveedhi, Sriram; Rogaway, Phillip (2013). "Garbling eficiente a partir de un cifrado de bloque de clave fija". Simposio IEEE sobre seguridad y privacidad de 2013. págs. 478–492. CiteSeerX 10.1.1.299.2755 . doi :10.1109/SP.2013.39. ISBN .  978-0-7695-4977-4.S2CID1351222  .​
10. Zahur, Samee; Rosulek, Mike; Evans, David (2015). Dos mitades forman un todo (PDF) .
11. Goldwasser, S; Micali, S; Rackoff, C (1985-12-01). "La complejidad del conocimiento de los sistemas de prueba interactivos". Actas del decimoséptimo simposio anual de la ACM sobre teoría de la computación - STOC '85 . Providence, Rhode Island, EE. UU.: Association for Computing Machinery. págs. 291–304. doi :10.1145/22145.22178. ISBN 978-0-89791-151-1.S2CID8689051  .​
12. Abascal, Jackson; Faghihi Sereshgi, Mohammad Hossein; Hazay, Carmit; Ishai, Yuval; Venkitasubramaniam, Muthuramakrishnan (30 de octubre de 2020). "¿Es práctico el paradigma GMW clásico? El caso de 2PC activamente seguro no interactivo". Actas de la Conferencia ACM SIGSAC de 2020 sobre seguridad informática y de las comunicaciones . CCS '20. Evento virtual, EE. UU.: Association for Computing Machinery. págs. 1591–1605. doi :10.1145/3372297.3423366. ISBN 978-1-4503-7089-9. Número de identificación del sujeto  226228208.
13. Lindell, Yehuda; Pinkas, Benny (2007). "Un protocolo eficiente para computación segura de dos partes en presencia de adversarios maliciosos". En Naor, Moni (ed.). Avances en criptología - EUROCRYPT 2007. Apuntes de clase en informática. Vol. 4515. Berlín, Heidelberg: Springer. págs. 52–78. Bibcode :2007LNCS.4515...52L. doi : 10.1007/978-3-540-72540-4_4 . ISBN 978-3-540-72540-4.
14. Ishai, Yuval; Kushilevitz, Eyal; Ostrovsky, Rafail; Prabhakaran, Manoj; Sahai, Amit (2011). "Computación segura no interactiva y eficiente". En Paterson, Kenneth G. (ed.). Avances en criptología – EUROCRYPT 2011. Apuntes de clase en informática. Vol. 6632. Berlín, Heidelberg: Springer. págs. 406–425. doi : 10.1007/978-3-642-20465-4_23 . ISBN . 978-3-642-20465-4.
15. Hazay, Carmit; Ishai, Yuval; Venkitasubramaniam, Muthuramakrishnan (2017). "Circuitos ilegibles de seguridad activa con sobrecarga de comunicación constante en el modelo simple". En Kalai, Yael; Reyzin, Leonid (eds.). Teoría de la criptografía . Apuntes de clase en informática. Vol. 10678. Cham: Springer International Publishing. págs. 3–39. doi :10.1007/978-3-319-70503-3_1. ISBN 978-3-319-70503-3.

Lectura adicional

• "El circuito confuso de Yao" (PDF) . CS598 . illinois.edu . Consultado el 18 de octubre de 2016 .