
En física , el óctuple sendero es un esquema organizativo para una clase de partículas subatómicas conocidas como hadrones que condujo al desarrollo del modelo de quarks . Tanto el físico estadounidense Murray Gell-Mann como el físico israelí Yuval Ne'eman propusieron la idea de forma independiente y simultánea en 1961. [1] [2] [a] El nombre proviene del artículo de Gell-Mann (1961) y es una alusión al Noble Óctuple Sendero del Budismo . [3]
En 1947, los físicos creían que tenían una buena comprensión de lo que eran los fragmentos más pequeños de materia. Había electrones , protones , neutrones y fotones (los componentes que forman la mayor parte de la experiencia cotidiana, como los átomos y la luz), junto con un puñado de partículas exóticas inestables (es decir, que sufren desintegración radiactiva ) necesarias para explicar las observaciones de rayos cósmicos, como piones , muones y el supuesto neutrino . Además, el descubrimiento del positrón sugirió que podría haber antipartículas para cada uno de ellos. Se sabía que debe existir una " interacción fuerte " para superar la repulsión electrostática en los núcleos atómicos. No todas las partículas están influenciadas por esta fuerza fuerte, pero las que lo están se denominan "hadrones", que ahora se clasifican además como mesones (masa media) y bariones (peso pesado).
Pero el descubrimiento del kaón neutro a finales de 1947 y el posterior descubrimiento de un kaón cargado positivamente en 1949 ampliaron la familia de los mesones de una manera inesperada y en 1950 la partícula lambda hizo lo mismo con la familia de los bariones. Estas partículas se desintegran mucho más lentamente de lo que se producen, una pista de que hay dos procesos físicos diferentes involucrados. Esto fue sugerido por primera vez por Abraham Pais en 1952. En 1953, Murray Gell-Mann y una colaboración en Japón, Tadao Nakano con Kazuhiko Nishijima , sugirieron de forma independiente un nuevo valor conservado ahora conocido como " extrañeza " durante sus intentos de comprender la creciente colección de partículas conocidas. [4] [5] [b] La tendencia de descubrir nuevos mesones y bariones continuaría durante la década de 1950 a medida que aumentaba el número de partículas "elementales" conocidas. Los físicos estaban interesados en comprender las interacciones hadrón-hadrón a través de la interacción fuerte. El concepto de isospín , introducido en 1932 por Werner Heisenberg poco después del descubrimiento del neutrón, se utilizó para agrupar algunos hadrones en "multipletes", pero hasta entonces ninguna teoría científica exitosa cubría los hadrones en su totalidad. Éste fue el comienzo de un período caótico en la física de partículas que se conoció como la era del " zoológico de partículas ". La vía óctuple representó un paso para salir de esta confusión y avanzar hacia el modelo de quarks , que resultó ser la solución.
La teoría de la representación de grupos es la base matemática detrás del método óctuple, pero no se necesitan estas matemáticas bastante técnicas para entender cómo ayuda a organizar las partículas. Las partículas se clasifican en grupos como mesones o bariones. Dentro de cada grupo, se separan aún más por su momento angular de espín . Aparecen patrones simétricos cuando se grafica la extrañeza de estos grupos de partículas frente a su carga eléctrica . (Esta es la forma más común de hacer estos gráficos hoy en día, pero originalmente los físicos usaban un par equivalente de propiedades llamadas hipercarga y espín isotópico , el último de los cuales ahora se conoce como isospín ). La simetría en estos patrones es un indicio de la simetría subyacente de la fuerte interacción entre las propias partículas. En los gráficos a continuación, los puntos que representan partículas que se encuentran a lo largo de la misma línea horizontal comparten la misma extrañeza, s , mientras que los que están en las mismas diagonales inclinadas hacia la izquierda comparten la misma carga eléctrica, q (dada como múltiplos de la carga elemental ).
En el método óctuple original, los mesones se organizaban en octetos y singletes. Esta es una de las diferencias más sutiles entre el método óctuple y el modelo de quarks que inspiró, que sugiere que los mesones deberían agruparse en nonets (grupos de nueve).

El método óctuple organiza ocho de los mesones con el espín más bajo -0 en un octeto. [1] [6] Son:
Las partículas diametralmente opuestas en el diagrama son antipartículas entre sí, mientras que las partículas en el centro son su propia antipartícula.
El mesón primo eta sin carga y sin elementos extraños fue clasificado originalmente por sí mismo como un singlete:
Según el modelo de quarks desarrollado posteriormente, se lo considera mejor como parte de un noneto mesónico, como se mencionó anteriormente.
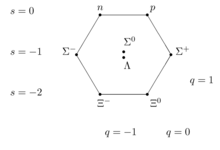
El óctuple camino organiza el giro - 1/ 2 bariones en un octeto. Consisten en

Los principios organizativos del camino óctuple también se aplican al giro .3/ 2 bariones, formando un decuplete .
Sin embargo, una de las partículas de este decuplete nunca había sido observada antes cuando se propuso la vía óctuple. Gell-Mann llamó a esta partícula la
Ohmio−
y predijo en 1962 que tendría una extrañeza de -3, carga eléctrica de -1 y una masa cercana1680 MeV/ c 2 . En 1964, un grupo de aceleradores de partículas de Brookhaven descubrió [7] una partícula que coincidía estrechamente con estas predicciones . Gell-Mann recibió el Premio Nobel de Física en 1969 por su trabajo sobre la teoría de partículas elementales .
Históricamente, los quarks fueron motivados por una comprensión de la simetría del sabor. Primero, se observó (1961) que los grupos de partículas estaban relacionados entre sí de una manera que coincidía con la teoría de representación de SU(3) . A partir de eso, se infirió que existe una simetría aproximada del universo que está parametrizada por el grupo SU(3). Finalmente (1964), esto condujo al descubrimiento de tres quarks ligeros (up, down y strange) intercambiados por estas transformaciones SU(3).
La vía óctuple puede entenderse en términos modernos como una consecuencia de las simetrías de sabor entre varios tipos de quarks . Dado que la fuerza nuclear fuerte afecta a los quarks de la misma manera independientemente de su sabor, reemplazar un sabor de quark por otro en un hadrón no debería alterar mucho su masa, siempre que las respectivas masas de quark sean menores que la escala de interacción fuerte, lo que se cumple para los tres quarks ligeros. Matemáticamente, este reemplazo puede describirse mediante elementos del grupo SU(3) . Los octetos y otras disposiciones de hadrones son representaciones de este grupo.
Existe un espacio vectorial tridimensional abstracto:
y las leyes de la física son aproximadamente invariantes al aplicar una transformación unitaria de determinante 1 a este espacio (a veces llamada rotación de sabor ):
Aquí, SU(3) se refiere al grupo de Lie de matrices unitarias 3×3 con determinante 1 ( grupo unitario especial ). Por ejemplo, la rotación de sabor
es una transformación que convierte simultáneamente todos los quarks up del universo en quarks down y viceversa. Más específicamente, estas rotaciones de sabor son simetrías exactas si solo se observan las interacciones de fuerza fuerte , pero no son simetrías verdaderamente exactas del universo porque los tres quarks tienen masas diferentes y diferentes interacciones electrodébiles.
Esta simetría aproximada se llama simetría de sabor , o más específicamente, simetría de sabor SU(3) .
Supongamos que tenemos una determinada partícula (por ejemplo, un protón) en un estado cuántico . Si aplicamos una de las rotaciones de sabor A a nuestra partícula, entra en un nuevo estado cuántico que podemos llamar . Dependiendo de A , este nuevo estado podría ser un protón, o un neutrón, o una superposición de un protón y un neutrón, o varias otras posibilidades. El conjunto de todos los estados cuánticos posibles abarca un espacio vectorial.
La teoría de la representación es una teoría matemática que describe la situación en la que los elementos de un grupo (aquí, las rotaciones de sabor A en el grupo SU(3)) son automorfismos de un espacio vectorial (aquí, el conjunto de todos los estados cuánticos posibles que se obtienen al rotar un protón según el sabor). Por lo tanto, al estudiar la teoría de la representación de SU(3), podemos aprender las posibilidades de lo que es el espacio vectorial y cómo se ve afectado por la simetría del sabor.
Dado que las rotaciones de sabor A son simetrías aproximadas, no exactas, cada estado ortogonal en el espacio vectorial corresponde a una especie de partícula diferente. En el ejemplo anterior, cuando un protón se transforma por cada posible rotación de sabor A , resulta que se mueve alrededor de un espacio vectorial de 8 dimensiones. Esas 8 dimensiones corresponden a las 8 partículas en el llamado "octeto bariónico" (protón, neutrón,
Σ+
,
Σ0
,
Σ−
,
Oh−
,
Oh0
,O). Esto corresponde a una representación de ocho dimensiones ("octeto") del grupo SU(3). Como A es una simetría aproximada, todas las partículas en este octeto tienen masas similares. [8]
Cada grupo de Lie tiene un álgebra de Lie correspondiente , y cada representación de grupo del grupo de Lie se puede mapear a una representación de álgebra de Lie correspondiente en el mismo espacio vectorial. El álgebra de Lie (3) se puede escribir como el conjunto de matrices hermíticas sin traza de 3×3 . Los físicos generalmente discuten la teoría de representación del álgebra de Lie (3) en lugar del grupo de Lie SU(3), ya que la primera es más simple y los dos son en última instancia equivalentes.
Después de la circulación de la versión preliminar de este trabajo (enero de 1961), el autor tuvo conocimiento de una teoría similar propuesta independientemente y simultáneamente por Y. Ne'eman ( Nuclear Physics , que se publicará próximamente). Y. Ohnuki informó sobre usos anteriores del grupo unitario tridimensional en relación con el modelo de Sakata en la Conferencia de Rochester de 1960 sobre Física de Altas Energías. A. Salam y J. Ward ( Nuovo Cimento , que se publicará próximamente) han considerado cuestiones relacionadas. El autor quisiera agradecer al Dr. Ne'eman y al Profesor Salam por comunicarle sus resultados.
Mientras que el final del artículo de Ne'eman (1961) dice:
Estoy en deuda con el profesor A. Salam por las discusiones sobre este problema. De hecho, cuando le presenté este artículo, me mostró un estudio que había realizado sobre la teoría unitaria del modelo de Sakata, tratado como un modelo de calibración y, por lo tanto, produciendo un conjunto similar de bosones vectoriales. Poco después de que se escribiera el presente artículo, nos llegó una versión posterior, que utilizaba la representación 8 para los bariones, como en este artículo, en una preimpresión del profesor M. Gell Mann .
Tras finalizar este trabajo, los autores supieron, a través de una carta privada del profesor Nambu al profesor Hayakawa, que el doctor Gell-Mann también había desarrollado una teoría similar.
referencia ligeramente irreverente al Noble Óctuple Sendero , un conjunto de principios para una vida correcta en el budismo .