En el campo matemático de la teoría de grafos , un grafo cero-simétrico es un grafo conexo en el que cada vértice tiene exactamente tres aristas incidentes y, por cada dos vértices, hay una simetría única que lleva un vértice al otro. Un grafo de este tipo es un grafo transitivo de vértices pero no puede ser un grafo transitivo de aristas : el número de simetrías es igual al número de vértices, demasiado pocos para llevar cada arista a cada una de las otras aristas. [1]
El nombre para esta clase de grafos fue acuñado por RM Foster en una carta de 1966 a HSM Coxeter . [2] En el contexto de la teoría de grupos , los grafos cero-simétricos también se denominan representaciones gráficas regulares de sus grupos de simetría. [3]
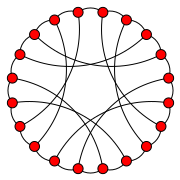
El gráfico cero-simétrico más pequeño es un gráfico no plano con 18 vértices. [4] Su notación MCF es [5,−5] 9 .
Entre los grafos planares , los grafos cuboctaédricos truncados y los grafos icosidodecaédricos truncados también son cero-simétricos. [5]
Todos estos ejemplos son grafos bipartitos . Sin embargo, existen ejemplos más grandes de grafos con simetría cero que no son bipartitos. [6]
Estos ejemplos también tienen tres clases de simetría diferentes (órbitas) de aristas. Sin embargo, existen grafos con simetría cero con solo dos órbitas de aristas. El grafo más pequeño de estos tiene 20 vértices, con notación MCF [6,6,-6,-6] 5 . [7]
Todo grafo cero-simétrico finito es un grafo de Cayley , una propiedad que no siempre se cumple para grafos cúbicos transitivos por vértices en general y que ayuda en la solución de tareas de enumeración combinatorias relacionadas con grafos cero-simétricos. Hay 97687 grafos cero-simétricos en hasta 1280 vértices. Estos grafos forman el 89% de los grafos cúbicos de Cayley y el 88% de todos los grafos cúbicos transitivos por vértices conectados en el mismo número de vértices. [8]
Todos los grafos cero-simétricos conexos finitos conocidos contienen un ciclo hamiltoniano , pero se desconoce si cada grafo cero-simétrico conexo finito es necesariamente hamiltoniano. [9] Este es un caso especial de la conjetura de Lovász de que (con cinco excepciones conocidas, ninguna de las cuales es cero-simétrica) cada grafo transitivo de vértice conexo finito y cada grafo de Cayley finito es hamiltoniano.