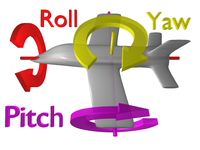


Una rotación de guiñada es un movimiento alrededor del eje de guiñada de un cuerpo rígido que cambia la dirección en la que apunta, hacia la izquierda o hacia la derecha de su dirección de movimiento. La velocidad de guiñada de un automóvil, una aeronave, un proyectil u otro cuerpo rígido es la velocidad angular de esta rotación o la tasa de cambio del ángulo de rumbo cuando la aeronave está en posición horizontal. Se mide comúnmente en grados por segundo o radianes por segundo.
Otro concepto importante es el momento de guiñada , o momento de guiñada, que es el componente de un par alrededor del eje de guiñada.
La velocidad de guiñada se puede medir midiendo la velocidad del suelo en dos puntos separados geométricamente de la carrocería, o mediante un giroscopio , o se puede sintetizar a partir de acelerómetros y similares. Es la medida principal de cómo los conductores perciben visualmente el giro de un automóvil.

Es importante en vehículos estabilizados electrónicamente . La velocidad de guiñada está directamente relacionada con la aceleración lateral del vehículo que gira a velocidad constante alrededor de un radio constante, por la relación
La convención de signos se puede establecer prestando una atención rigurosa a los sistemas de coordenadas.
En una maniobra más general donde el radio varía y/o la velocidad varía, la relación anterior ya no se cumple.
La velocidad de guiñada se puede medir con acelerómetros en el eje vertical. Cualquier dispositivo destinado a medir la velocidad de guiñada se denomina sensor de velocidad de guiñada .
Estudiar la estabilidad de un vehículo de carretera requiere una aproximación razonable a las ecuaciones de movimiento.

El diagrama ilustra un vehículo de cuatro ruedas, en el que el eje delantero está situado a un metro por delante del centro de gravedad y el eje trasero está a b metros hacia atrás desde el centro de gravedad. La carrocería del coche apunta en una dirección (theta) mientras que se desplaza en una dirección (psi). En general, no son lo mismo. El neumático se desliza en la región del punto de contacto en la dirección de desplazamiento, pero los cubos están alineados con la carrocería del vehículo, con la dirección en posición central. Los neumáticos se deforman a medida que giran para adaptarse a esta desalineación y, como consecuencia, generan fuerzas laterales.
A partir del estudio de estabilidad direccional , denotando la velocidad angular , las ecuaciones de movimiento son:
con la masa del vehículo, la velocidad del vehículo y el ángulo general del vehículo.
El coeficiente de se denominará " amortiguación " por analogía con un amortiguador de masa-resorte que tiene una ecuación de movimiento similar. Por la misma analogía, el coeficiente de se denominará "rigidez", ya que su función es devolver el sistema a una deflexión cero, de la misma manera que un resorte.
La forma de la solución depende únicamente de los signos de los términos de amortiguamiento y rigidez. Los cuatro tipos de soluciones posibles se presentan en la figura.
La única solución satisfactoria requiere que tanto la rigidez como la amortiguación sean positivas. Si el centro de gravedad está por delante del centro de la distancia entre ejes , este valor siempre será positivo y el vehículo será estable a todas las velocidades. Sin embargo, si se encuentra más atrás, el valor puede volverse negativo por encima de una velocidad dada por:
Por encima de esta velocidad, el vehículo será inestable en cuanto a dirección (guiñada) . Las correcciones para el efecto relativo de los neumáticos delanteros y traseros y las fuerzas de dirección están disponibles en el artículo principal.
Estas rotaciones son rotaciones intrínsecas y el cálculo que las sustenta es similar a las fórmulas de Frenet-Serret . Realizar una rotación en un sistema de referencia intrínseco equivale a multiplicar por la derecha su matriz característica (la matriz que tiene como columnas el vector del sistema de referencia) por la matriz de la rotación.
El primer avión que demostró un control activo sobre los tres ejes fue el planeador de los hermanos Wright de 1902. [1]