Un cartograma (también llamado mapa de área de valor o mapa anamórfico , este último común entre los hablantes de alemán) es un mapa temático de un conjunto de características (países, provincias, etc.), en el que su tamaño geográfico se altera para que sea directamente proporcional a una variable seleccionada, como el tiempo de viaje, la población o el ingreso nacional bruto . El espacio geográfico en sí mismo se deforma, a veces extremadamente, para visualizar la distribución de la variable. Es uno de los tipos de mapa más abstractos ; de hecho, algunas formas pueden llamarse más apropiadamente diagramas . Se utilizan principalmente para mostrar énfasis y para análisis como nomogramas . [1]
Los cartogramas aprovechan el hecho de que el tamaño es la variable visual más intuitiva para representar una cantidad total. [2] En esto, es una estrategia similar a los mapas de símbolos proporcionales , que escalan las características de puntos, y muchos mapas de flujo , que escalan el peso de las características lineales. Sin embargo, estas dos técnicas solo escalan el símbolo del mapa , no el espacio en sí; un mapa que se extiende a lo largo de las características lineales se considera un cartograma lineal (aunque se pueden agregar técnicas de mapas de flujo adicionales). Una vez construidos, los cartogramas se utilizan a menudo como base para otras técnicas de mapeo temático para visualizar variables adicionales, como el mapeo coroplético .

El cartograma se desarrolló más tarde que otros tipos de mapas temáticos , pero siguió la misma tradición de innovación en Francia . [3] El cartograma más antiguo conocido fue publicado en 1876 por el estadístico y geógrafo francés Pierre Émile Levasseur , quien creó una serie de mapas que representaban a los países de Europa como cuadrados, dimensionados según una variable y dispuestos en su posición geográfica general (con mapas separados escalados por área, población, seguidores religiosos y presupuesto nacional). [4] Los revisores posteriores han llamado a sus figuras un diagrama estadístico en lugar de un mapa, pero Levasseur se refirió a él como un carte figurative , el término común entonces en uso para cualquier mapa temático. Los produjo como material de enseñanza, reconociendo inmediatamente el poder intuitivo del tamaño como variable visual: "Es imposible que el niño no se sorprenda por la importancia del comercio de Europa occidental en relación con el de Europa oriental, que no se dé cuenta de cuánto Inglaterra, que tiene un territorio pequeño pero supera a otras naciones por su riqueza y especialmente por su marina, cuánto, por el contrario, Rusia que, por su superficie y su población ocupa el primer lugar, todavía está por detrás de otras naciones en el comercio y la navegación".
La técnica de Levasseur no parece haber sido adoptada por otros, y aparecen relativamente pocos mapas similares durante muchos años. El siguiente desarrollo notable fue un par de mapas de Hermann Haack y Hugo Weichel de los resultados electorales de 1898 para el Reichstag alemán en preparación para la elección de 1903 , el cartograma contiguo más antiguo conocido . [5] Ambos mapas mostraban un esquema similar del Imperio alemán, con uno subdividido en distritos electorales a escala y el otro distorsionando los distritos electorales por área. La posterior expansión de áreas densamente pobladas alrededor de Berlín , Hamburgo y Sajonia tenía como objetivo visualizar la controvertida tendencia de los socialdemócratas principalmente urbanos a ganar el voto popular, mientras que el Zentrum principalmente rural ganó más escaños (presagiando así la popularidad moderna de los cartogramas para mostrar las mismas tendencias en elecciones recientes en los Estados Unidos). [6]
El cartograma continuo surgió poco después en los Estados Unidos, donde apareció una variedad en los medios populares después de 1911. [7] [8] La mayoría fueron dibujados de manera bastante tosca en comparación con Haack y Weichel, con la excepción de los "cartogramas estadísticos rectangulares" del maestro cartógrafo estadounidense Erwin Raisz , quien afirmó haber inventado la técnica. [9] [10]
Cuando Haack y Weichel se refirieron a su mapa como un kartogramm , este término se usaba comúnmente para referirse a todos los mapas temáticos, especialmente en Europa. [11] [12] No fue hasta que Raisz y otros cartógrafos académicos manifestaron su preferencia por un uso restringido del término en sus libros de texto (Raisz inicialmente defendió el cartograma de área de valor ) que el significado actual se adoptó gradualmente. [13] [14]
El principal desafío de los cartogramas siempre ha sido la elaboración de las formas distorsionadas, lo que los convierte en un objetivo primordial para la automatización informática. Waldo R. Tobler desarrolló uno de los primeros algoritmos en 1963, basado en una estrategia de deformación del espacio en sí mismo en lugar de los distintos distritos. [15] Desde entonces, se han desarrollado una amplia variedad de algoritmos (ver más abajo), aunque todavía es común elaborar cartogramas manualmente. [1]
Desde los primeros días del estudio académico de los cartogramas, estos han sido comparados con las proyecciones de mapas de muchas maneras, en el sentido de que ambos métodos transforman (y por lo tanto distorsionan) el espacio mismo. [15] El objetivo de diseñar un cartograma o una proyección de mapa es, por lo tanto, representar uno o más aspectos de los fenómenos geográficos con la mayor precisión posible, al tiempo que se minimiza el daño colateral de la distorsión en otros aspectos. En el caso de los cartogramas, al escalar las características para que tengan un tamaño proporcional a una variable distinta de su tamaño real, el peligro es que las características se distorsionen hasta el punto de que ya no sean reconocibles para los lectores de mapas, lo que las hace menos útiles.
Al igual que con las proyecciones de mapas, las compensaciones inherentes a los cartogramas han dado lugar a una amplia variedad de estrategias, incluidos métodos manuales y docenas de algoritmos informáticos que producen resultados muy diferentes a partir de los mismos datos de origen. La calidad de cada tipo de cartograma se juzga normalmente en función de la precisión con la que escala cada característica, así como de cómo (y qué tan bien) intenta preservar alguna forma de reconocibilidad en las características, normalmente en dos aspectos: forma y relación topológica (es decir, adyacencia retenida de características vecinas). [16] [17] Es probable que sea imposible preservar ambas, por lo que algunos métodos de cartograma intentan preservar una a expensas de la otra, algunos intentan una solución de compromiso para equilibrar la distorsión de ambas, y otros métodos no intentan preservar ninguna de las dos, sacrificando toda la reconocibilidad para lograr otro objetivo.

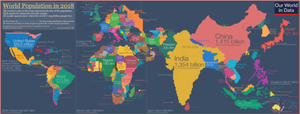
El cartograma de área es, con diferencia, la forma más común; escala un conjunto de características de la región, normalmente distritos administrativos como condados o países, de modo que el área de cada distrito sea directamente proporcional a una variable dada. Por lo general, esta variable representa el recuento o la cantidad total de algo, como la población total , el producto interior bruto o el número de puntos de venta de una marca o tipo determinado. También se pueden utilizar otras variables de razón estrictamente positivas , como el PIB per cápita o la tasa de natalidad , pero a veces pueden producir resultados engañosos debido a la tendencia natural a interpretar el tamaño como la cantidad total. [2] De estas, la población total es probablemente la variable más común, a veces denominada mapa isodemográfico .
Las diversas estrategias y algoritmos se han clasificado de varias maneras, generalmente de acuerdo con sus estrategias con respecto a la preservación de la forma y la topología. Aquellos que preservan la forma a veces se denominan equiformes , aunque isomorfos (misma forma) u homomórficos (forma similar) pueden ser términos más adecuados. Tres categorías amplias son ampliamente aceptadas: contiguos (preservan la topología, distorsionan la forma), no contiguos (preservan la forma, distorsionan la topología) y diagramáticos (distorsionan ambas). Recientemente, taxonomías más exhaustivas de Nusrat y Kobourov, Markowska y otros se han basado en este marco básico en un intento de capturar la variedad de enfoques que se han propuesto y en las apariencias de los resultados. [18] [19] Las diversas taxonomías tienden a coincidir en los siguientes tipos generales de cartogramas de área.
Este es un tipo de cartograma contiguo que utiliza una única fórmula matemática paramétrica (como una superficie curva polinómica ) para distorsionar el espacio mismo para igualar la distribución espacial de la variable elegida, en lugar de distorsionar las características individuales. Debido a esta distinción, algunos han preferido llamar al resultado un pseudocartograma . [20] El primer algoritmo de cartograma informático de Tobler se basó en esta estrategia, [15] [21] para el cual desarrolló la construcción matemática general en la que se basan sus algoritmos y los posteriores. [15] Este enfoque primero modela la distribución de la variable elegida como una función de densidad continua (generalmente utilizando un ajuste de mínimos cuadrados ), luego utiliza la inversa de esa función para ajustar el espacio de modo que la densidad se iguale. El algoritmo de Gastner-Newman, una de las herramientas más populares utilizadas hoy en día, es una versión más avanzada de este enfoque. [22] [23] Debido a que no escalan directamente los distritos, no hay garantía de que el área de cada distrito sea exactamente igual a su valor.

También llamados cartogramas irregulares o cartogramas de deformación , [19] Esta es una familia de algoritmos muy diferentes que escalan y deforman la forma de cada distrito mientras mantienen los bordes adyacentes. Este enfoque tiene sus raíces en los cartogramas de principios del siglo XX de Haack y Weichel y otros, aunque estos rara vez fueron tan matemáticamente precisos como las versiones computarizadas actuales. La variedad de enfoques que se han propuesto incluyen autómatas celulares , particiones de árboles cuádruples , generalización cartográfica , ejes mediales , fuerzas similares a resortes y simulaciones de inflación y deflación. [18] Algunos intentan preservar alguna apariencia de la forma original (y por lo tanto pueden denominarse homomórficos ), [25] pero estos son a menudo algoritmos más complejos y lentos que los que distorsionan severamente la forma.

Este es quizás el método más simple para construir un cartograma, en el que cada distrito simplemente se reduce o se amplía en tamaño según la variable sin alterar su forma en absoluto. [16] En la mayoría de los casos, un segundo paso ajusta la ubicación de cada forma para reducir los espacios y superposiciones entre las formas, pero sus límites en realidad no son adyacentes. Si bien la preservación de la forma es una ventaja principal de este enfoque, los resultados a menudo tienen una apariencia aleatoria porque los distritos individuales no encajan bien entre sí.

En este enfoque, cada distrito se reemplaza por una forma geométrica simple de tamaño proporcional. De esta manera, la forma original se elimina por completo y la contigüidad puede conservarse de forma limitada o no conservarse en absoluto. Aunque generalmente se los conoce como cartogramas de Dorling después de que el algoritmo de Daniel Dorling de 1996 facilitara por primera vez su construcción, [26] en realidad son la forma original de cartograma, que se remonta a Levasseur (1876) [4] y Raisz (1934). [9] Hay varias opciones disponibles para las formas geométricas:
Debido a que los distritos no son en absoluto reconocibles, este enfoque es más útil y popular para situaciones en las que las formas no serían familiares para los lectores de mapas de todos modos (por ejemplo, distritos electorales parlamentarios del Reino Unido ) o donde los distritos son tan familiares para los lectores de mapas que su distribución general es información suficiente para reconocerlos (por ejemplo, países del mundo). Por lo general, este método se utiliza cuando es más importante para los lectores determinar el patrón geográfico general que identificar distritos particulares; si se necesita identificación, a menudo se etiquetan las formas geométricas individuales.

En este enfoque (también llamado cartogramas de bloques o regulares ), cada forma no solo se escala o se deforma, sino que se reconstruye a partir de una teselación discreta del espacio, generalmente en cuadrados o hexágonos. Cada celda de la teselación representa un valor constante de la variable (por ejemplo, 5000 residentes), por lo que se puede calcular el número de celdas completas que se ocuparán (aunque el error de redondeo a menudo significa que el área final no es exactamente proporcional a la variable). Luego se ensambla una forma a partir de esas celdas, generalmente con algún intento de conservar la forma original, incluyendo características salientes como panhandles que ayudan al reconocimiento (por ejemplo, Long Island y Cape Cod a menudo se exageran). Por lo tanto, estos cartogramas suelen ser homomórficos y al menos parcialmente contiguos.
Este método funciona mejor con variables que ya se miden como un entero de valor relativamente bajo, lo que permite una coincidencia uno a uno con las celdas. Esto los ha hecho muy populares para visualizar el Colegio Electoral de los Estados Unidos que determina la elección del presidente , apareciendo en la cobertura televisiva y en numerosos sitios web de seguimiento de votos. [27] Varios ejemplos de cartogramas de bloques fueron publicados durante la temporada de elecciones presidenciales estadounidenses de 2016 por The Washington Post , [28] el blog FiveThirtyEight , [29] y el Wall Street Journal , [30] entre otros. Este es un cartograma para las elecciones de 2024 y 2028, basado en la distribución de votos del Censo de 2020:

La principal desventaja de este tipo de cartogramas ha sido tradicionalmente que debían construirse manualmente, pero recientemente se han desarrollado algoritmos para generar automáticamente cartogramas de mosaico tanto cuadrados como hexagonales. [31] [32]

Mientras que un cartograma de área manipula el área de una entidad poligonal, un cartograma lineal manipula la distancia lineal en una entidad lineal. La distorsión espacial permite al lector de mapas visualizar fácilmente conceptos intangibles como el tiempo de viaje y la conectividad en una red. Los cartogramas de distancia también son útiles para comparar dichos conceptos entre diferentes entidades geográficas. Un cartograma de distancia también puede denominarse cartograma de punto central .
Un uso común de los cartogramas de distancia es mostrar los tiempos de viaje relativos y las direcciones desde los vértices de una red. Por ejemplo, en un cartograma de distancia que muestra el tiempo de viaje entre ciudades, cuanto menos tiempo se necesite para ir de una ciudad a otra, más corta será la distancia en el cartograma. Cuando se tarda más tiempo en viajar entre dos ciudades, se mostrarán más alejadas en el cartograma, incluso si están físicamente cerca una de otra.
Los cartogramas de distancia también se utilizan para mostrar la conectividad. Esto es común en los mapas de metro y subterráneo, donde las estaciones y paradas se muestran a la misma distancia en el mapa, aunque la distancia real varía. Aunque el tiempo exacto y la distancia de un lugar a otro están distorsionados, estos cartogramas siguen siendo útiles para viajes y análisis.

Tanto los cartogramas de área como los lineales ajustan la geometría base del mapa, pero ninguno tiene requisitos sobre cómo se simboliza cada característica. Esto significa que la simbología se puede utilizar para representar una segunda variable utilizando un tipo diferente de técnica de mapeo temático . [16] Para los cartogramas lineales, el ancho de línea se puede escalar como un mapa de flujo para representar una variable como el volumen de tráfico. Para los cartogramas de área, es muy común rellenar cada distrito con un color como un mapa coroplético . Por ejemplo, WorldMapper ha utilizado esta técnica para mapear temas relacionados con problemas sociales globales, como la pobreza o la desnutrición; un cartograma basado en la población total se combina con una coropleta de una variable socioeconómica, lo que brinda a los lectores una visualización clara del número de personas que viven en condiciones desfavorecidas.
Otra opción para los cartogramas diagramáticos es subdividir las formas en gráficos (comúnmente un gráfico circular ), de la misma manera que se hace a menudo con los mapas de símbolos proporcionales. Esto puede ser muy eficaz para mostrar variables complejas como la composición de la población, pero puede resultar abrumador si hay una gran cantidad de símbolos o si los símbolos individuales son muy pequeños.
Uno de los primeros cartógrafos que generó cartogramas con la ayuda de la visualización por computadora fue Waldo Tobler, de la Universidad de California en Santa Bárbara , en la década de 1960. Antes del trabajo de Tobler, los cartogramas se creaban a mano (y, ocasionalmente, todavía se hacen). El Centro Nacional de Información y Análisis Geográfico, ubicado en el campus de la UCSB, mantiene una Central de Cartogramas en línea, archivada el 5 de octubre de 2016 en Wayback Machine , con recursos relacionados con los cartogramas.
Varios paquetes de software generan cartogramas. La mayoría de las herramientas de generación de cartogramas disponibles funcionan junto con otras herramientas de software SIG como complementos o producen de forma independiente resultados cartográficos a partir de datos SIG formateados para funcionar con productos SIG de uso común. Algunos ejemplos de software de cartogramas son ScapeToad, [33] [34] Cart, [35] y Cartogram Processing Tool (un ArcScript para ArcGIS de ESRI ), que utilizan el algoritmo Gastner-Newman. [36] [37] Un algoritmo alternativo, Carto3F, [38] también se implementa como un programa independiente para uso no comercial en plataformas Windows. [39] Este programa también proporciona una optimización del algoritmo original de hoja de goma de Dougenik. [40] [41] El paquete CRAN recmap proporciona una implementación de un algoritmo de cartograma rectangular. [42]
