Un calendario perpetuo es un calendario válido por muchos años, generalmente diseñado para buscar el día de la semana de una fecha determinada en el pasado o en el futuro.
Para los calendarios gregoriano y juliano , un calendario perpetuo normalmente consta de una de tres variaciones generales:
Este calendario perpetuo no indica las fechas de fiestas movibles como la Pascua , que se calculan en base a una combinación de eventos del año trópico y de ciclos lunares. Estas cuestiones se tratan con gran detalle en Computus .
Un ejemplo temprano de un calendario perpetuo para uso práctico se encuentra en el Nürnberger Handschrift GNM 3227a . El calendario cubre el período de 1390 a 1495 (por lo que el manuscrito está fechado en c. 1389). Para cada año de este período, enumera el número de semanas entre Navidad y Quinquagesima . Este es el primer ejemplo conocido de una forma tabular de calendario perpetuo que permite el cálculo de las fiestas movibles que se hicieron populares durante el siglo XV. [5]
La capilla Cappella dei Mercanti, en Turín, contiene una máquina de calendario perpetuo realizada por Giovanni Plana utilizando tambores giratorios.

Las oficinas y los establecimientos minoristas a menudo muestran dispositivos que contienen un conjunto de elementos para formar todos los números posibles del 1 al 31, así como los nombres/abreviaturas de los meses y los días de la semana, para mostrar la fecha actual para conveniencia de las personas que podrían estar firmando y fechando documentos como cheques . Los establecimientos que sirven bebidas alcohólicas pueden usar una variante que muestra el mes y el día actuales pero restando la edad legal para el consumo de alcohol en años, lo que indica la última fecha de nacimiento legal para las compras de alcohol. Un dispositivo común consiste en dos cubos en un soporte. Un cubo lleva los dígitos del cero al cinco. El otro lleva los dígitos 0, 1, 2, 6 (o 9 si está invertido), 7 y 8. Esto es suficiente porque solo uno y dos pueden aparecer dos veces en la fecha y están en ambos cubos, mientras que el 0 está en ambos cubos para que todas las fechas de un solo dígito se puedan mostrar en formato de dos dígitos. Además de los dos cubos, hay tres bloques, cada uno de ellos tan ancho como los dos cubos juntos, y un tercero de la misma altura y profundidad, que tienen impresos los nombres de los meses en sus caras largas. El mes actual está girado hacia adelante en el bloque delantero, con los otros dos bloques de meses detrás de él.
Algunas reformas del calendario han sido etiquetadas como calendarios perpetuos porque sus fechas se fijan en los mismos días de la semana todos los años. Algunos ejemplos son el Calendario Mundial , el Calendario Fijo Internacional y el Calendario Pax . Técnicamente, estos no son calendarios perpetuos sino calendarios perennes . Su propósito, en parte, es eliminar la necesidad de tablas de calendario perpetuo, algoritmos y dispositivos de cálculo.

En relojería , el término «calendario perpetuo» describe un mecanismo de calendario que muestra correctamente la fecha en el reloj «de forma perpetua», teniendo en cuenta las diferentes duraciones de los meses y los años bisiestos. El mecanismo interno moverá la esfera al día siguiente. [6]
Los calendarios perpetuos utilizan algoritmos para calcular el día de la semana de un año, mes y día del mes determinados. Aunque las operaciones individuales de las fórmulas se pueden implementar de forma muy eficiente en software, son demasiado complicadas para que la mayoría de las personas puedan realizar todos los cálculos mentalmente. [7] Los diseñadores de calendarios perpetuos ocultan la complejidad en tablas para simplificar su uso.
Un calendario perpetuo emplea una tabla para determinar cuál de los catorce calendarios anuales se debe utilizar. Una tabla para el calendario gregoriano expresa su gran ciclo de 400 años: 303 años comunes y 97 años bisiestos suman un total de 146.097 días, o exactamente 20.871 semanas. Este ciclo se divide en un período de 100 años con 25 años bisiestos, lo que da 36.525 días, o un día menos que 5.218 semanas completas; y tres períodos de 100 años con 24 años bisiestos cada uno, lo que da 36.524 días, o dos días menos que 5.218 semanas completas.
Dentro de cada bloque de 100 años, la naturaleza cíclica del calendario gregoriano procede de la misma manera que su predecesor juliano: un año común comienza y termina el mismo día de la semana, por lo que el año siguiente comenzará el siguiente día sucesivo de la semana. Un año bisiesto tiene un día más, por lo que el año posterior a un año bisiesto comienza el segundo día de la semana después de que comenzó el año bisiesto. Cada cuatro años, el día de la semana inicial avanza cinco días, por lo que durante un período de 28 años, avanza 35, volviendo al mismo lugar tanto en la progresión del año bisiesto como en el día de la semana inicial. Este ciclo se completa tres veces en 84 años, lo que deja 16 años en el cuarto ciclo incompleto del siglo.
Un factor importante que complica la construcción de un algoritmo de calendario perpetuo es la duración peculiar y variable de febrero, que en un momento fue el último mes del año, dejando los primeros 11 meses de marzo a enero con un patrón de repetición de cinco meses: 31, 30, 31, 30, 31, ..., de modo que la diferencia con marzo del día de inicio de la semana para cualquier mes podría determinarse fácilmente. La congruencia de Zeller , un algoritmo bien conocido para encontrar el día de la semana para cualquier fecha, define explícitamente enero y febrero como los meses "13.º" y "14.º" del año anterior para aprovechar esta regularidad, pero el cálculo dependiente del mes sigue siendo muy complicado para la aritmética mental:
En cambio, un calendario perpetuo basado en tablas proporciona un mecanismo de búsqueda simple para encontrar la diferencia entre el día de la semana y el primer día de cada mes. Para simplificar la tabla, en un año bisiesto, enero y febrero deben considerarse como un año independiente o tener entradas adicionales en la tabla de meses:
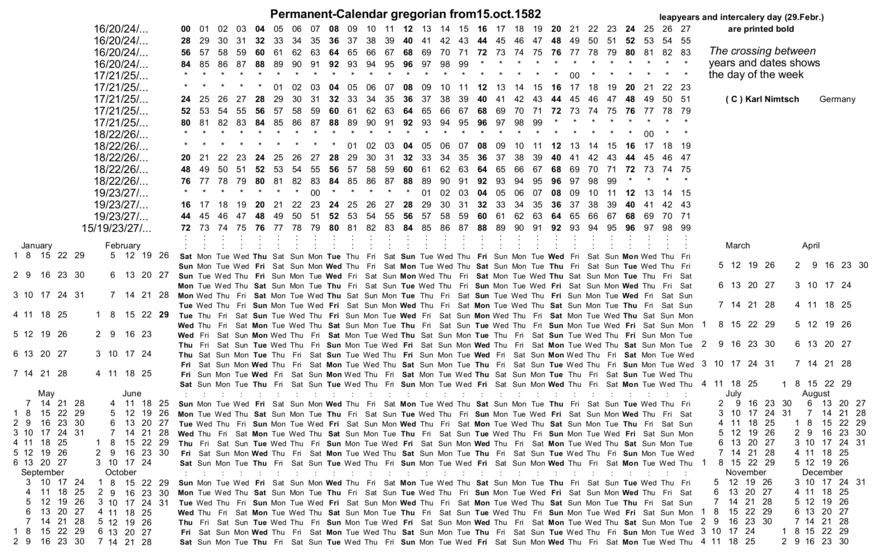
El siguiente calendario funciona para cualquier fecha a partir del 15 de octubre de 1582 en adelante, pero solo para las fechas del calendario gregoriano.