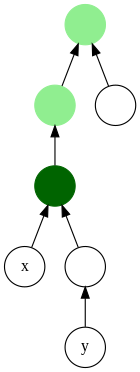
En teoría de grafos e informática , el ancestro común más bajo ( LCA ) (también llamado ancestro menos común ) de dos nodos v y w en un árbol o gráfico acíclico dirigido (DAG) T es el nodo más bajo (es decir, el más profundo) que tiene ambos v. y w como descendientes, donde definimos cada nodo como descendiente de sí mismo (por lo que si v tiene una conexión directa con w , w es el ancestro común más bajo).
El LCA de v y w en T es el ancestro compartido de v y w que se encuentra más alejado de la raíz. El cálculo de los ancestros comunes más bajos puede ser útil, por ejemplo, como parte de un procedimiento para determinar la distancia entre pares de nodos en un árbol: la distancia de v a w se puede calcular como la distancia de la raíz a v , más la distancia desde la raíz hasta w , menos el doble de la distancia desde la raíz hasta su ancestro común más bajo (Djidjev, Pantziou y Zaroliagis 1991).
En una estructura de datos de árbol donde cada nodo apunta a su padre, el ancestro común más bajo se puede determinar fácilmente encontrando la primera intersección de las rutas desde v y w hasta la raíz. En general, el tiempo de cálculo requerido para este algoritmo es O(h) , donde h es la altura del árbol (longitud del camino más largo desde una hoja hasta la raíz). Sin embargo, existen varios algoritmos para procesar árboles de modo que los ancestros comunes más bajos puedan encontrarse más rápidamente. El algoritmo de ancestros comunes más bajos fuera de línea de Tarjan , por ejemplo, preprocesa un árbol en tiempo lineal para proporcionar consultas de ACV en tiempo constante. En general, existen algoritmos similares en los DAG, pero con una complejidad superlineal.
El problema del ancestro común más bajo fue definido por Alfred Aho , John Hopcroft y Jeffrey Ullman (1973), pero Dov Harel y Robert Tarjan (1984) fueron los primeros en desarrollar una estructura de datos de ancestro común más bajo óptimamente eficiente. Su algoritmo procesa cualquier árbol en tiempo lineal, utilizando una fuerte descomposición de rutas , de modo que las consultas posteriores del ancestro común más bajo puedan responderse en un tiempo constante por consulta. Sin embargo, su estructura de datos es compleja y difícil de implementar. Tarjan también encontró un algoritmo más simple pero menos eficiente, basado en la estructura de datos de búsqueda de unión , para calcular los ancestros comunes más bajos de un lote de pares de nodos fuera de línea .
Baruch Schieber y Uzi Vishkin (1988) simplificaron la estructura de datos de Harel y Tarjan, dando lugar a una estructura implementable con el mismo preprocesamiento asintótico y límites de tiempo de consulta. Su simplificación se basa en el principio de que, en dos tipos especiales de árboles, los ancestros comunes más bajos son fáciles de determinar: si el árbol es un camino, entonces el ancestro común más bajo puede calcularse simplemente a partir del mínimo de los niveles de los dos niveles consultados. nodos, mientras que si el árbol es un árbol binario completo , los nodos pueden indexarse de tal manera que los ancestros comunes más bajos se reduzcan a simples operaciones binarias en los índices. La estructura de Schieber y Vishkin descompone cualquier árbol en una colección de caminos, de modo que las conexiones entre los caminos tienen la estructura de un árbol binario, y combina ambas técnicas de indexación más simples.
Omer Berkman y Uzi Vishkin (1993) descubrieron una forma completamente nueva de responder consultas de ancestros comunes más bajos, logrando nuevamente un tiempo de preprocesamiento lineal con un tiempo de consulta constante. Su método implica formar un recorrido de Euler de un gráfico formado a partir del árbol de entrada duplicando cada borde y usar este recorrido para escribir una secuencia de números de nivel de los nodos en el orden en que los visita el recorrido; una consulta del ancestro común más bajo se puede transformar en una consulta que busca el valor mínimo que ocurre dentro de algún subintervalo de esta secuencia de números. Luego manejan este problema de consulta de rango mínimo (RMQ) combinando dos técnicas, una basada en el cálculo previo de las respuestas a intervalos grandes que tienen tamaños que son potencias de dos, y la otra basada en la búsqueda de tablas para consultas de intervalos pequeños. Este método fue presentado posteriormente de forma simplificada por Michael Bender y Martin Farach-Colton (2000). Como habían observado previamente Gabow, Bentley y Tarjan (1984), el problema de rango mínimo puede a su vez transformarse nuevamente en un problema de ancestro común más bajo utilizando la técnica de los árboles cartesianos .
Alstrup et al. hicieron más simplificaciones. (2004) y Fischer y Heun (2006).
Sleator y Tarjan (1983) propusieron la variante dinámica de LCA del problema en la que la estructura de datos debe estar preparada para manejar consultas de LCA entremezcladas con operaciones que cambian el árbol (es decir, reorganizar el árbol agregando y eliminando bordes). Esta variante se puede solucionar a tiempo en el tamaño total del árbol para todas las modificaciones y consultas. Esto se hace manteniendo el bosque utilizando la estructura de datos de árboles dinámicos con partición por tamaño; esto luego mantiene una descomposición ligera de cada árbol y permite que las consultas de ACV se realicen en tiempo logarítmico en el tamaño del árbol.
Como se mencionó anteriormente, LCA se puede reducir primero a RMQ, luego dividir la secuencia de números en intervalos y aplicar dos técnicas diferentes para manejar consultas de rango mínimo en diferentes intervalos y manejar consultas de rango mínimo dentro de un intervalo.
La reducción del ACV a RMQ comenzó caminando por el árbol. Al recorrer el árbol se registra el orden de las etiquetas y la profundidad del nodo visitado. Luego, se puede responder una pregunta de LCA respondiendo una pregunta de RMQ cuya entrada de un problema de RMQ son los índices de dos nodos secundarios en la lista de nodos visitados.

Por lo tanto, LCA se puede resolver resolviendo RMQ.
A pesar de que existe una solución de tiempo y espacio lineal constante para RMQ general, se puede aplicar una solución simplificada que haga uso de las propiedades de LCA. Esta solución simplificada solo se puede utilizar para RMQ reducidos de LCA.
De manera similar a la solución mencionada anteriormente, dividimos la secuencia en cada bloque , donde cada bloque tiene un tamaño de .

Al dividir la secuencia en bloques, la consulta se puede resolver resolviendo dos casos diferentes:
Para responder a la consulta en el caso uno, hay 3 grupos de variables precalculadas para ayudar a reducir el tiempo de consulta.
Primero, el elemento mínimo con el índice más pequeño en cada bloque se calcula previamente y se denota como . Un conjunto de ocupa espacio.
En segundo lugar, dado el conjunto de , la consulta RMQ para este conjunto se calcula previamente utilizando la solución con tiempo constante y espacio linealítmico . Hay bloques, por lo que la tabla de búsqueda de esa solución ocupa espacio. Porque , = espacio. Por lo tanto, la consulta RMQ precalculada que utiliza la solución con tiempo constante y espacio linealítmico en estos bloques solo ocupa espacio.
En tercer lugar, en cada bloque , sea un índice tal que . Para todos desde hasta , el bloque se divide en dos intervalos y . Luego se calcula previamente el elemento mínimo con el índice más pequeño para los intervalos en y en cada bloque . Estos elementos mínimos se denominan prefijo min para el intervalo en y sufijo min para el intervalo en . Cada iteración de calcula un par de prefijo min y sufijo min. Por lo tanto, el número total de minutos de prefijo y minutos de sufijo en un bloque es . Dado que hay bloques, en total, todas las matrices de prefijo mínimo y sufijo mínimo toman espacios .
En total, se necesita espacio para almacenar los 3 grupos de variables precalculadas mencionados anteriormente.
Por lo tanto, responder la consulta en el caso 1 es simplemente plantear el mínimo de las siguientes tres preguntas:
Sea el bloque que contiene el elemento en index y para index .
Las 3 preguntas se pueden responder en tiempo constante. Por tanto, el caso 1 puede responderse en espacio lineal y tiempo constante.
La secuencia de RMQ que se redujo de LCA tiene una propiedad que una RMQ normal no tiene. El siguiente elemento siempre es +1 o -1 del elemento actual. Por ejemplo:

Por lo tanto, cada bloque se puede codificar como una cadena de bits donde 0 representa la profundidad actual -1 y 1 representa la profundidad actual +1. Esta transformación convierte un bloque en una cadena de bits de tamaño . Una cadena de bits de tamaño tiene posibles cadenas de bits. Desde entonces .
Por lo tanto, siempre hay una de las posibles cadenas de bits con un tamaño de .
Luego, para cada posible cadena de bits, aplicamos la ingenua solución de tiempo constante de espacio cuadrático . Esto ocupará espacios, que es .
Por lo tanto, responder la consulta en el caso 2 es simplemente encontrar el bloque correspondiente (en el que hay una cadena de bits) y realizar una búsqueda en la tabla para esa cadena de bits. Por tanto, el caso 2 se puede resolver utilizando un espacio lineal con un tiempo de búsqueda constante.
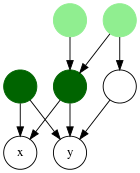
Si bien se estudió originalmente en el contexto de los árboles, la noción de ancestros comunes más bajos se puede definir para gráficos acíclicos dirigidos (DAG), utilizando cualquiera de dos definiciones posibles. En ambos, se supone que los bordes del DAG apuntan de padres a hijos.
En un árbol, el ancestro común más bajo es único; en un DAG de n nodos, cada par de nodos puede tener hasta n -2 LCA (Bender et al. 2005), mientras que la existencia de un LCA para un par de nodos ni siquiera está garantizada en DAG conectados arbitrariamente.
Aït-Kaci et al. ofrecen un algoritmo de fuerza bruta para encontrar los ancestros comunes más bajos. (1989): encuentra todos los ancestros de x e y , luego devuelve el elemento máximo de la intersección de los dos conjuntos. Existen mejores algoritmos que, de forma análoga a los algoritmos de ACV en árboles, preprocesan un gráfico para permitir consultas de ACV en tiempo constante. El problema de la existencia de LCA se puede resolver de manera óptima para DAG dispersos mediante un algoritmo O (| V || E |) debido a Kowaluk y Lingas (2005).
Dash et al. (2013) presentan un marco unificado para el preprocesamiento de gráficos acíclicos dirigidos para calcular un ancestro común más bajo representativo en un DAG enraizado en tiempo constante. Su marco puede lograr tiempos de preprocesamiento casi lineales para gráficos dispersos y está disponible para uso público. [1]
El problema de calcular los ancestros comunes más bajos de las clases en una jerarquía de herencia surge en la implementación de sistemas de programación orientados a objetos (Aït-Kaci et al. 1989). El problema del ACV también encuentra aplicaciones en modelos de sistemas complejos que se encuentran en la computación distribuida (Bender et al. 2005).