
En teoría de grafos , una contracción de aristas es una operación que elimina una arista de un grafo y, al mismo tiempo, fusiona los dos vértices que unía previamente. La contracción de aristas es una operación fundamental en la teoría de menores de grafos . La identificación de vértices es una forma menos restrictiva de esta operación.
La operación de contracción de arista ocurre en relación a una arista particular, . La arista se elimina y sus dos vértices incidentes, y , se fusionan en un nuevo vértice , donde las aristas incidentes a cada una corresponden a una arista incidente a o . De manera más general, la operación puede realizarse en un conjunto de aristas contrayendo cada arista (en cualquier orden). [1]
El gráfico resultante a veces se escribe como . (Compare esto con , que significa simplemente eliminar el borde sin fusionar sus vértices incidentes).
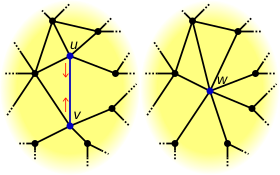
Como se define a continuación, una operación de contracción de aristas puede dar como resultado un gráfico con múltiples aristas incluso si el gráfico original era un gráfico simple . [2] Sin embargo, algunos autores [3] no permiten la creación de múltiples aristas, de modo que las contracciones de aristas realizadas en gráficos simples siempre producen gráficos simples.
Sea un grafo ( o grafo dirigido ) que contiene una arista con . Sea una función que mapea cada vértice en en sí mismo, y en caso contrario, lo mapea a un nuevo vértice . La contracción de da como resultado un nuevo grafo , donde , , y para cada , es incidente a una arista si y solo si, la arista correspondiente, es incidente a en .
La identificación de vértices (a veces llamada contracción de vértices ) elimina la restricción de que la contracción debe ocurrir sobre vértices que comparten una arista incidente. (Por lo tanto, la contracción de aristas es un caso especial de identificación de vértices). La operación puede ocurrir en cualquier par (o subconjunto) de vértices en el grafo. Las aristas entre dos vértices en contracción a veces se eliminan. Si y son vértices de componentes distintos de , entonces podemos crear un nuevo grafo identificando y en como un nuevo vértice en . [4] De manera más general, dada una partición del conjunto de vértices, uno puede identificar vértices en la partición; el grafo resultante se conoce como grafo cociente .
La división de vértices , que es lo mismo que la división de vértices, significa que un vértice se divide en dos, donde estos dos nuevos vértices son adyacentes a los vértices a los que estaba adyacente el vértice original. Esta es una operación inversa a la identificación de vértices, aunque en general para la identificación de vértices, los vértices adyacentes de los dos vértices identificados no son el mismo conjunto.
La contracción de la trayectoria se produce en el conjunto de aristas de una trayectoria que se contraen para formar una única arista entre los puntos finales de la trayectoria. Las aristas que inciden en los vértices a lo largo de la trayectoria se eliminan o se conectan de manera arbitraria (o sistemática) a uno de los puntos finales.
Considérense dos grafos disjuntos y , donde contiene vértices y y contiene vértices y . Supongamos que podemos obtener el grafo identificando los vértices de y de como el vértice de e identificando los vértices de y de como el vértice de . En una torsión de con respecto al conjunto de vértices , identificamos, en cambio, con y con . [5]
Tanto las técnicas de contracción de aristas como de vértices son valiosas para demostrar por inducción el número de vértices o aristas de un gráfico, donde se puede suponer que una propiedad se cumple para todos los gráficos más pequeños y esto se puede usar para demostrar la propiedad para el gráfico más grande.
La contracción de aristas se utiliza en la fórmula recursiva para el número de árboles de expansión de un gráfico conectado arbitrario , [6] y en la fórmula de recurrencia para el polinomio cromático de un gráfico simple. [7]
Las contracciones también son útiles en estructuras en las que deseamos simplificar un grafo identificando vértices que representan entidades esencialmente equivalentes. Uno de los ejemplos más comunes es la reducción de un grafo dirigido general a un grafo dirigido acíclico contrayendo todos los vértices de cada componente fuertemente conexo . Si la relación descrita por el grafo es transitiva , no se pierde información siempre que etiquetemos cada vértice con el conjunto de etiquetas de los vértices que se contrajeron para formarlo.
Otro ejemplo es la coalescencia realizada en la asignación de registros de coloración de gráficos globales , donde los vértices se contraen (cuando es seguro) para eliminar operaciones de movimiento entre variables distintas.
La contracción de bordes se utiliza en paquetes de modelado 3D (ya sea manualmente o a través de alguna función del software de modelado) para reducir consistentemente el número de vértices, lo que ayuda en la creación de modelos con pocos polígonos.