En matemáticas , dos funciones tienen un contacto de orden k si, en un punto P , tienen el mismo valor y sus primeras k derivadas son iguales. Se trata de una relación de equivalencia , cuyas clases de equivalencia se denominan generalmente jets . El punto de osculación también se denomina doble cúspide . El contacto es una noción geométrica; se puede definir algebraicamente como una valoración .
También se habla de curvas y objetos geométricos que tienen contacto de orden k en un punto: esto también se llama osculación (es decir, beso), generalizando la propiedad de ser tangente . (Aquí las derivadas se consideran con respecto a la longitud del arco). Una curva osculante de una familia dada de curvas es una curva que tiene el mayor orden posible de contacto con una curva dada en un punto dado; por ejemplo, una línea tangente es una curva osculante de la familia de líneas y tiene contacto de primer orden con la curva dada; un círculo osculante es una curva osculante de la familia de círculos y tiene contacto de segundo orden (mismo ángulo tangente y curvatura), etc. [1]
Las formas de contacto son formas diferenciales particulares de grado 1 en variedades de dimensión impar; véase geometría de contacto . Las transformaciones de contacto son cambios relacionados de coordenadas, de importancia en la mecánica clásica . Véase también transformación de Legendre .
El contacto entre variedades se estudia a menudo en la teoría de singularidades , donde se clasifican los tipos de contacto, estos incluyen la serie A (A0 : cruce, A1 : tangente, A2 : osculador, ...) y la serie umbilical o D donde hay un alto grado de contacto con la esfera.
Se dice que dos curvas en el plano que se intersecan en un punto p tienen:
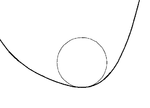

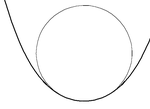
Para cada punto S ( t ) de una curva plana suave S , existe exactamente un círculo osculador cuyo radio es el recíproco de κ( t ), la curvatura de S en t . Cuando la curvatura es cero (en un punto de inflexión de la curva), el círculo osculador es una línea recta. El lugar geométrico de los centros de todos los círculos osculadores (también llamados "centros de curvatura") es la evoluta de la curva.
Si la derivada de curvatura κ'( t ) es cero, entonces el círculo osculador tendrá contacto de tercer orden y se dice que la curva tiene un vértice . La evoluta tendrá una cúspide en el centro del círculo. El signo de la segunda derivada de curvatura determina si la curva tiene un mínimo o máximo local de curvatura. Todas las curvas cerradas tendrán al menos cuatro vértices, dos mínimos y dos máximos (el teorema de los cuatro vértices ).
En general, una curva no tendrá contacto de cuarto orden con ningún círculo. Sin embargo, el contacto de cuarto orden puede ocurrir de manera genérica en una familia de curvas de un parámetro, en una curva de la familia donde (a medida que varía el parámetro) dos vértices (uno máximo y otro mínimo) se unen y se aniquilan. En esos puntos, la segunda derivada de la curvatura será cero.
Los círculos que tienen dos puntos de contacto con dos puntos S ( t 1 ), S ( t 2 ) en una curva son círculos bitangentes . Los centros de todos los círculos bitangentes forman el conjunto de simetría . El eje medial es un subconjunto del conjunto de simetría.